Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 94 Tập 2 Cánh diều

    Với giải bài tập Toán lớp 10 trang 94 Tập 2 trong Bài 6: Ba đường conic sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 94 Tập 2.

    1 409 12/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 94 Tập 2

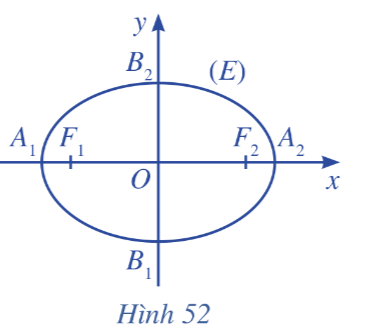
    Hoạt động 2 trang 94 Toán 10 Tập 2: Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF1 + MF2 = 2a, ở đó F1F2 = 2c (với a > c > 0).

    Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của F1F2, trục Oy là đường trung trực của F1F2 và F2 nằm trên tia Ox (Hình 52). Khi đó, F1(– c; 0) và F2(c; 0) là hai tiêu điểm của elip (E). Chứng minh rằng:

    a) A1(– a; 0) và A2(a; 0) đều là giao điểm của elip (E) với trục Ox.

    b) B1(0; – b) và B2(0; b), ở đó b=a2−c2, đều là giao điểm của elip (E) với trục Oy.

    Giải Toán 10 Bài 6 (Cánh diều): Ba đường conic (ảnh 1) 

    Lời giải

    a) A1F1=−c−−a2+0−02=−c+a=a−c (vì a > c > 0 nên a – c > 0).

    A1F2=c−−a2+0−02=a+c=a+c

    Suy ra A1F1 + A2F2 = (a – c) + (a + c) = 2a.

    Vậy điểm A1(– a; 0) thuộc elip (E).

    Mà A1(– a; 0) thuộc trục Ox nên A1(– a; 0) là giao điểm của elip (E) với trục Ox.

    Tương tự, ta chứng minh được A2(a; 0) là giao điểm của elip (E) với trục Ox.

    b) Ta có:

    B2F1=−c−02+0−b2=c2+b2=a2=a=a

    (vì b=a2−c2 nên b2=a2−c2⇔a2=b2+c2 và a > 0 nên |a| = a).

    Tương tự: B2F2=c−02+0−b2=c2+b2=a2=a (do a > 0).

    Suy ra B2F1 = B2F2 = a nên B2F1 + B2F2 = a + a = 2a.

    Do đó, B2(0; b) thuộc elip (E).

    Mà B2(0; b) thuộc trung Oy nên B2(0; b) là giao điểm của elip (E) với trục Oy.

    Tương tự, ta chứng minh được: B1(0; – b) là giao điểm của elip (E) với trục Oy.

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Giải Toán 10 trang 93 Tập 2

    Giải Toán 10 trang 94 Tập 2

    Giải Toán 10 trang 95 Tập 2

    Giải Toán 10 trang 96 Tập 2

    Giải Toán 10 trang 97 Tập 2

    Giải Toán 10 trang 98 Tập 2

    Giải Toán 10 trang 99 Tập 2

    Giải Toán 10 trang 100 Tập 2

    Giải Toán 10 trang 102 Tập 2

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Bài tập cuối chương 7

    Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng

    Bài 1: Mệnh đề toán học

    Bài 2: Tập hợp. Các phép toán trên tập hợp

    Bài tập cuối chương 1 trang 19

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 409 12/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: