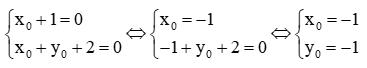Chứng tỏ đồ thị hàm số y = (m – 1)x + m – 2 luôn đi qua một điểm cố định
Lời giải Bài 7 trang 13 SBT Toán 8 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.
Giải SBT Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Bài 7 trang 13 SBT Toán 8 Tập 2: Chứng tỏ đồ thị hàm số y = (m – 1)x + m – 2 luôn đi qua một điểm cố định.
Lời giải:
Giả sử điểm cố định của đồ thị hàm số y = (m – 1)x + m – 2 là I(x0; y0).
Thay x = x0 và y = y0 vào y = (m – 1)x + m – 2, ta được:
y0 = (m – 1)x0 + m – 2
mx0 – x0 + m – 2 – y0 = 0
m(x0 + 1) – (y0 + x0 + 2) = 0 (1)
Để (1) luôn đúng với mọi giá trị của m thì
Vậy đồ thị hàm số y = (m – 1)x + m – 2 luôn đi qua điểm cố định I(–1; –1).
Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 3 trang 13 SBT Toán 8 Tập 2: Tìm giao điểm của đường thẳng d: y = 2 – 4x.....
Bài 5 trang 13 SBT Toán 8 Tập 2: Cho đồ thị của hàm số y = ax đi qua điểm A(2; – 4)....
Bài 6 trang 13 SBT Toán 8 Tập 2: Cho hàm số y = 3x + 6....
Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Hệ số góc của đường thẳng
Bài tập cuối chương 5 trang 18
Bài 1: Phương trình bậc nhất một ẩn
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 8 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 8 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 8 - Chân trời sáng tạo
- Giải SBT Ngữ văn 8 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Soạn văn 8 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 8 – Friends Plus
- Giải sbt Tiếng Anh 8 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 8 Friends plus đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 8 Friends plus đầy đủ nhất
- Giải sgk Khoa học tự nhiên 8 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 8 – Chân trời sáng tạo
- Giải sgk Lịch sử 8 – Chân trời sáng tạo
- Lý thuyết Lịch sử 8 - Chân trời sáng tạo
- Giải sbt Lịch sử 8 – Chân trời sáng tạo
- Giải sgk Địa lí 8 – Chân trời sáng tạo
- Lý thuyết Địa lí 8 - Chân trời sáng tạo
- Giải sbt Địa lí 8 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 8 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sgk Công nghệ 8 – Chân trời sáng tạo
- Lý thuyết Công nghệ 8 - Chân trời sáng tạo
- Giải sbt Công nghệ 8 – Chân trời sáng tạo
- Giải sgk Tin học 8 – Chân trời sáng tạo
- Lý thuyết Tin học 8 - Chân trời sáng tạo
- Giải sbt Tin học 8 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 8 – Chân trời sáng tạo