Nội dung bài viết

    Xem thêm

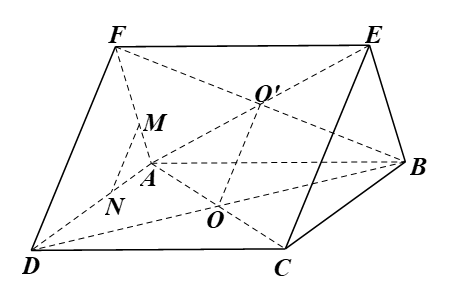
    Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O'

    Lời giải Bài 2 trang 121 SBT Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 492 20/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 3: Đường thẳng và mặt phẳng song song

    Bài 2 trang 121 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.

    a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).

    b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho AM = 13AF, AN = 13AD Chứng minh MN // (DCEF).

    Lời giải:

    Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng

    a) Do O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.

    Xét trong ∆BDF có: O, O’ lần lượt là trung điểm của BD, BF nên OO’ là đường trung bình của ∆BDF, suy ra OO’ // DF (1)

    Tương tự, trong ∆ACE ta cũng có OO’ // CE (2)

    Từ (1) và (2) suy ra OO’ // DF // CE, mà DF ⊂ (ADF), CE ⊂ (BCE)

    Suy ra OO’ song song với các mặt phẳng (ADF) và (BCE).

    b) Do AM = 13AF, AN = 13AD nên AMAF=ANAD=13

    Xét ∆ADF có AMAF=ANAD suy ra MN // DF (định lý Thalès đảo)

    Mà DF ⊂ (DCEF), suy ra MN // (DCEF).

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 121 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác ABD và ACD....

    Bài 2 trang 121 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’....

    Bài 3 trang 122 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi G là trọng tâm của tam giác SAB...

    Bài 4 trang 122 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm...

    Bài 5 trang 122 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi (α) là mặt phẳng đi qua trung điểm M...

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

    Bài 2: Hai đường thẳng song song

    Bài 4: Hai mặt phẳng song song

    Bài 5: Phép chiếu song song

    Bài tập cuối chương 4 trang 132

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 492 20/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: