TOP 40 câu Trắc nghiệm Ôn tập chương 2 (có đáp án 2024) – Toán 9

Trắc nghiệm Toán lớp 9 Ôn tập chương 2

Câu 1: Đường tròn là hình:

A. Không có trục đối xứng

B. Có một trục đối xứng

C. Có hai trục đối xứng

C. Có vô số trục đối xứng

Hiển thị đáp án

Đáp án: D

Giải thích:

Đường tròn có trục đối xứng là đường thẳng đi qua tâm của nó. Do có vô số đường kính nên đường tròn có vô số trục đối xứng

Câu 2: Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax và By (Ax và By và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax và By theo thứ tự tại C và D. Lấy I là trung điểm của CD. Chọn câu sai:

A. Đường tròn có đường kính CD và tiếp xúc với AB

B. Đường tròn có đường kính CD cắt AB

C. IO $\perp$ AB

D. IO = $\frac{DC}{2}$

Hiển thị đáp án

Đáp án: B

Giải thích:

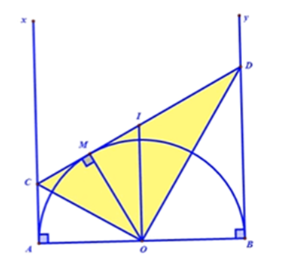
Vì I là trung điểm CD

Nên I là tâm của đường tròn đường kính CD

Theo tính chất hai tiếp tuyến cắt nhau:

AC = CM và BD = DM

Xét tứ giác ABDC có:

AC // BD $\Rightarrow$ ABDC là hình thang

Suy ra IO là đường trung bình của hình thang ABDC

$\Rightarrow$IO // AC // BD mà AC$\perp$AB$\Rightarrow$IO$\perp$AB (1)

IO = $\frac{AC+BD}{2}=\frac{CM+DM}{2}=\frac{CD}{2}$ (2)

Từ (1) và (2) suy ra đường tròn đường kính CD tiếp xúc với AB

Vậy A, C, D đúng, B sai

Câu 3: Đường tròn tâm O bán kính 5cm là tập hợp các điểm:

A. Có khoảng cách đến điểm O nhỏ hơn bằng 5cm

B. Có khoảng cách đến O bằng 5cm

C. Cách đều O một khoảng là 5cm

D. Cả B và C đều đúng

Hiển thị đáp án

Đáp án: D

Giải thích:

Tập hợp các điểm cách O một khoảng 5cm được gọi là đường tròn tâm O bán kính 5cm nên B, C đúng

Tập hợp các điểm cách O một khoảng nhỏ hơn hoặc bằng 5cm được gọi là hình tròn tâm O bán kính 5cm nên A sai

Câu 4: Hai tiếp tuyến tại A và B của đường tròn (O; R) cắt nhau tại M. Nếu MA = R$\sqrt{3}$ thì góc $\widehat{AOB}$ bằng:

A. 120^o

B. 90^o

C. 60^o

D. 45^o

Hiển thị đáp án

Đáp án: A

Giải thích:

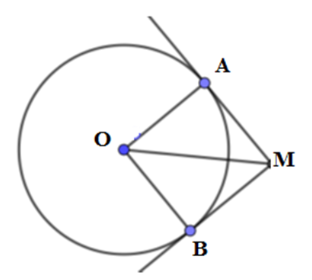
Có AM là tiếp tuyến của đường tròn (O)

nên AM vuông góc với OA

Xét tam giác AOM vuông tại A

nên có tan$\widehat{AOM}$ =$\frac{AM}{OA}=\frac{R\sqrt{3}}{R}=\sqrt{3}$

$\Rightarrow \widehat{AOM}$ = 60^o

Mà hai tiếp tuyến AM và BM cắt nhau tại M nên ta có OM là phân giác của $\widehat{AOB}$

Vậy $\widehat{AOB}$ = 2 $\widehat{AOM}$ = 2.60^o = 120^o

Câu 5: Cho (O; R) và đường thẳng a, gọi d là khoảng cách từ O đến a. Phát biểu nào sau đây là sai:

A. Nếu d < R, thì đường thẳng a cắt đường tròn (O)

B. Nếu d > R, thì đường thẳng a không cắt đường tròn (O)

C. Nếu d = R thì đường thẳng a đi qua tâm O của đường tròn

D. Nếu d = R thì đường thẳng a tiếp xúc với đường tròn (O)

Hiển thị đáp án

Đáp án: C

Giải thích:

Nếu d = R thì đường thẳng a tiếp xúc với đường tròn (O) nên C sai, D đúng

Câu 6: Chọn câu sai:

A. Hai đường tròn cắt nhau thì đường nối tâm là trung trực của dây cung

B. Qua ba điểm không thẳng hàng, ta luôn xác định được một đường tròn

C. Hai đường tròn tiếp xúc nhau, điểm tiếp xúc nằm trên đường nối tâm

D. Tâm của đường tròn nội tiếp tam giác là giao điểm của ba đường trung trực

Hiển thị đáp án

Đáp án: D

Giải thích:

Hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây cung (đúng)

Qua ba điểm không thẳng hàng, ta luôn xác định được một đường tròn (đường tròn ngoại tiếp tam giác)

Hai đường tròn tiếp xúc nhau, điểm tiếp xúc nằm trên đường nối tâm (đúng)

Tâm của đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác nên D sai

Câu 7: Cho hình vuông nội tiếp đường tròn (O; R). Chu vi của hình vuông là:

A. 2R$\sqrt{2}$

B. 3R$\sqrt{2}$

C. 4R$\sqrt{2}$

D. 6R

Hiển thị đáp án

Đáp án: C

Giải thích:

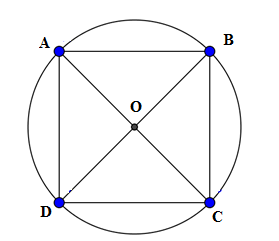
Hình vuông ABCD nội tiếp đường tròn tâm O

Khi đó đường chéo BD là đường kính của (O)

Suy ra BD = 2R

Xét tam giác BDC vuông cân tại C,

theo định lý Pytago ta có:

BC² + CD² = BD²

$\iff$ 2BC² = 4R² $\Rightarrow$ BC = R$\sqrt{2}$

Chu vi hình vuông ABCD là 4R$\sqrt{2}$

*Chú ý:

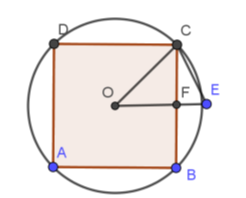
Câu 8: Trong hình vẽ bên cho OC$\perp$AB, AB = 12cm, OA = 10cm.

Độ dài AC là:

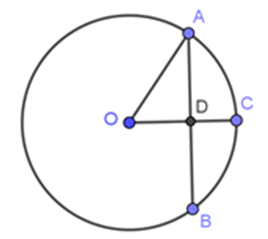
A. 8cm

B. 2$\sqrt{10}$cm

C. 4$\sqrt{7}$cm

D. 2cm

Hiển thị đáp án

Đáp án: B

Giải thích:

Vì OC vuông góc với AB nên D là trung điểm của AB (mối quan hệ giữa đường kính và dây)

AD = $\frac{AB}{2}=\frac{12}{2}$ = 6cm

Xét tam giác AOD vuông tại D nên

OD² = OA² – AD² = 10² – 6² = 64

$\Rightarrow$OD = 8cm

Có OD + DC = OC nên

DC = OC – OD = 10 – 8 = 2cm

Xét tam giác ADC vuông tại D nên

AC² = AD² + DC² = 6² + 2² = 40

Vậy AC = 2$\sqrt{10}$cm

Câu 9: Cho hai đường tròn (O; 4cm) và (O’; 3cm) biết OO’ = 5cm. Hai đường tròn cắt nhau tại A và B. Độ dài AB là:

A. 2,4cm

B. 4,8cm

C. $\frac{5}{12}$ cm

D. 5cm

Hiển thị đáp án

Đáp án: B

Giải thích:

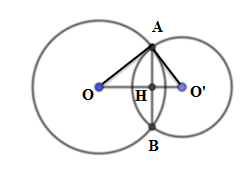
Xét tam giác OAO’ có

OA² + O’A² = OO’² (vì 4² + 3² = 5²) nên tam giác OAO’ vuông tại A

Xét tam giác OAO’ có AH là đường cao nên

AH.OO’ = OA.OA’

$\Rightarrow$ AH = $\frac{OA.O\text{'}A}{OO\text{'}}=\frac{4.3}{5}=\frac{12}{5}$

Mà AB = 2AH nên AB = $\frac{25}{4}$= 4,8cm

Câu 10: Cho tam giác ABC cân tại đỉnh A, nội tiếp đường tròn (O). Phát biểu nào sau đây là đúng?

A. Tiếp tuyến tại A với đường tròn (O) là đường thẳng qua A và vuông góc với AB

B. Tiếp tuyến tại A của đường tròn (O) là đường thẳng qua A và vuông góc với AC

C. Tiếp tuyến tại A với đường tròn (O) là đường thẳng qua A và song song với BC

D. Cả 3 câu A, B, C đều sai

Hiển thị đáp án

Đáp án: C

Giải thích:

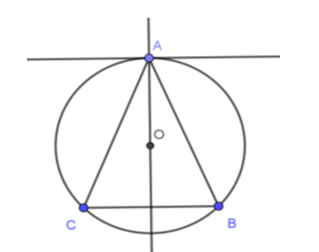
Vì tam giác ABC cân tại A nên tâm đường tròn ngoại tiếp nằm trên đường cao của tam giác đi qua A, hay OA vuông góc với BC mà tiếp tuyến của (O) tại A thì cũng phải vuông góc với OA (tính chất tiếp tuyến của đường tròn).

Vì vậy tiếp tuyến tại A của đường tròn sẽ song song với BC

Câu 11: Cho hai đường tròn (O; 5) và (O’; 5) cắt nhau tại A và B. Biết OO’ = 8. Độ dài dây cung AB là:

A. 6cm

B. 7cm

C. 5cm

D. 8cm

Hiển thị đáp án

Đáp án: A

Giải thích:

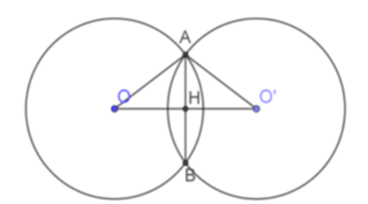
Ta có OA = O’A = 5cm nên tam giác AOO’ cân tại A.

Mà AH vuông góc với OO’ nên H là trung điểm của OO’.

Suy ra OH = 4cm

Xét tam giác AOH vuông tại H nên suy ra

AH² = OA² – OH² = 5² – 4² = 9 = 3²

Vậy AH = 3cm

Mà AB = 2AH (mối quan hệ giữa đường nối tâm và dây cung)

Vậy AB = 6cm

Câu 12: Phát biểu nào sau đây là sai:

A. Đường kính đi qua trung điểm của dây cung thì vuông góc với dây ấy

B. Đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy

C. Đường kính đi qua trung điểm của một dây (dây không đi qua tâm) thì vuông góc với dây ấy

D. Đường kính vuông góc với một dây thì hai đầu mút của dây ấy đối xứng qua đường kính này

Hiển thị đáp án

Đáp án: A

Giải thích:

Đường kính đi qua trung điểm của một dây chưa chắc đã vuông góc với dây ấy (trường hợp dây là đường kính của đường tròn)

Câu 13: Cho đường tròn (O; 25cm) và dây AB bằng 40cm. Khi đó khoảng cách từ tâm O đến dây AB là:

A. 15cm

B. 7cm

C. 20cm

D. 24cm

Hiển thị đáp án

Đáp án: A

Giải thích:

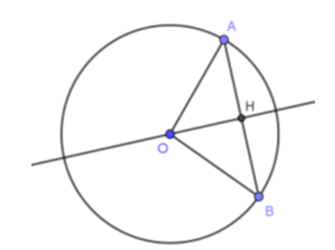
Từ O kẻ OH vuông góc với AB

Vậy H là trung điểm của AB (mối quan hệ giữa đường kính và dây)

suy ra AH = $\frac{AB}{2}$ = 20cm

Xét tam giác OAH vuông tại H nên theo định lý Pytago ta có:

OH² = OA² – AH²

= 25² – 20² = 225 = 15²

Vậy OH = 15cm

Câu 14: Cho đường tròn (O; 3cm), lấy điểm A sao cho OA = 6cm. Từ A vẽ tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Chu vi tam giác ABC là:

A. 9cm

B. 9$\sqrt{3}$cm

C. 9$\sqrt{2}$ cm

D. Kết quả khác

Hiển thị đáp án

Đáp án: B

Giải thích:

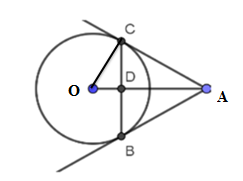
Gọi D là giao điểm của BC và OA

Có OC$\perp$ AC (tính chất tiếp tuyến của đường tròn)

Xét OAC vuông tại C, ta có:

OC² + CA² = OA² (Pytago)

$\Rightarrow$AC² = OA² − OC² = 6² − 3²

= 36 – 9 = 27

$\Rightarrow$ AC = 3$\sqrt{3}$ cm

Mà AC = AB (tính chất hai tiếp tuyến cắt nhau)

nên AB = 3 cm

Vì AC = AB; OB = OC

nên OA là đường trung trực của BC

hay OA $\perp$ BC tại D và D là trung điểm của CB

Xét tam giác vuông OCA có CD là đường cao nên:

CD = $\frac{OC.CA}{OA}=\frac{3.3\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}$

$\Rightarrow$ BC = 2CD = 3$\sqrt{3}$ cm

Vậy chu vi tam giác ABC là:

3$\sqrt{3}$+ 3$\sqrt{3}$+ 3$\sqrt{3}$ = 9cm

Câu 15: Cho tam giác ABC có AB = 5, AC = 12, BC = 13. Khi đó:

A. AB là tiếp tuyến của đường tròn (C; 5)

B. AC là tiếp tuyến của đường tròn (B; 5)

C. AB là tiếp tuyến của đường tròn (B; 12)

D. AC là tiếp tuyến của đường tròn (C; 13)

Hiển thị đáp án

Đáp án: B

Giải thích:

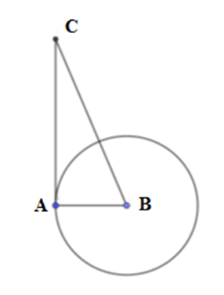
Xét ABC có:

AB² + AC² = 5² + 12²

= 169 = 13² = BC²

Áp dụng định lý Pytago đảo ta có ABC vuông tại A.

Do đó AB $\perp$ AC

AB là tiếp tuyến của đường tròn (C; 12)

AC là tiếp tuyến của đường tròn (B; 5)

Câu 16: Hai tiếp tuyến tại hai điểm B, C của một đường tròn (O) cắt nhau tại A tạo thành $\widehat{BAC}$ = 50^o. Số đo của góc $\widehat{BOC}$ bằng:

A. 30^o

B. 40^o

C. 130^o

D. 310^o

Hiển thị đáp án

Đáp án: C

Giải thích:

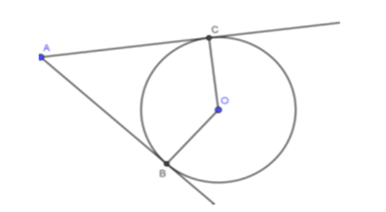
Vì hai tiếp tuyến của đường tròn (O) cắt nhau tại A

nên $\widehat{ACO}=\widehat{ABO}$ = 90^o

$\Rightarrow \widehat{CAB}+\widehat{COB}$ = 360^o – 180^o = 180^o

Mà $\widehat{CAB}$ = 50^o

nên $\widehat{COB}$ = 180^o – 50^o = 130^o

Câu 17: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B$\in$(O) và C$\in$(O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I. Tính độ dài BC biết OA = 9cm, O’A = 4cm

A. 12cm

B. 18cm

C. 10cm

D. 6cm

Hiển thị đáp án

Đáp án: A

Giải thích:

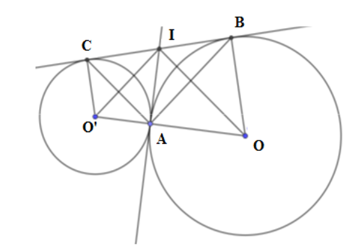
Ta có IO là tia phân giác của $\widehat{BIA}$ (tính chất hai tiếp tuyến cắt nhau)

IO’ là tia phân giác của $\widehat{CIA}$ (tính chất hai tiếp tuyến cắt nhau)

Mà $\widehat{BIA}+\widehat{CIA}$= 180^o $\Rightarrow \widehat{OIO\text{'}}$ = 90^o

Tam giác OIO’ vuông tại I có IA là đường cao (vì IA là tiếp tuyến chung của hai đường tròn) nên theo hệ thức lượng trong tam giác vuông ta có:

IA² = AO.AO’ = 9.4 = 36 $\Rightarrow$ IA = 6cm

$\Rightarrow$IA = IB = IC = 6cm (tính chất hai tiếp tuyến cắt nhau)

Vậy BC = 2IA = 2.6 = 12 (cm)

Câu 18: Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax và By (Ax và By và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax và By theo thứ tự tại C và D. Lấy I là trung điểm của CD. Hình thang ABDC có chu vi nhỏ nhất là:

A. AB

B. 2AB

C. 3AB

D. 4AB

Hiển thị đáp án

Đáp án: C

Giải thích:

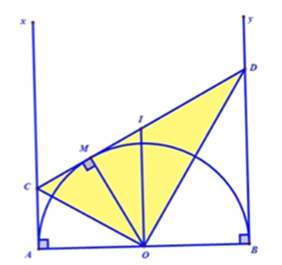
Theo tính chất hai tiếp tuyến cắt nhau:

AC = CN và BD = DM

Chu vi hình thang ABDC là:

P_ABDC = AC + AB + BD + CD

= CM + AB + DM + CD

= AB + 2CD

$\Rightarrow$ P_{ABDC min} khi CD_min

$\Rightarrow$ CD = AB $\Rightarrow$CD // AB

Mà OM $\perp$ CD $\Rightarrow$ OM$\perp$AB

P_{ABDC min} = AB + 2AB = 3AB

Vậy chu vi nhỏ nhất của hình thang ABDC là

3AB khi OM$\perp$ AB

Câu 19: Số tâm đối xứng của đường tròn là:

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.

Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn

Câu 20: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn

A. Đường tròn không có trục đối xứng

B. Đường tròn có duy nhất một trục đối xứng là đường kính

C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau

D. Đường tròn có vô số trục đối xứng là đường kính

Hiển thị đáp án

Đáp án: D

Câu 21: Tâm của đường tròn ngoại tiếp tam giác là:

A. Giao của ba đường phân giác

B. Giao của ba đường trung trực

C. Giao của ba đường cao

D. Giao của ba đường trung tuyến

Hiển thị đáp án

Đáp án: B

Giải thích: Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó

Câu 22: Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?

A. Điểm M nằm ngoài đường tròn

B. Điểm M nằm trên đường tròn

C.Điểm M nằm trong đường tròn

D. Điểm M không thuộc đường tròn

Hiển thị đáp án

Đáp án: B

Câu 23: Tâm của đường tròn ngoại tiếp tam giác vuông là

A. Trung điểm cạnh huyền

B. Trung điểm cạnh góc vuông lớn hơn

C. Giao ba đường cao

D. Giao ba đường trung tuyến

Hiển thị đáp án

Đáp án: A

Câu 24: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a

A. Tâm là giao điểm A và bán kính R =$a\sqrt{2}$

B. Tâm là giao điểm hai đường chéo và bán kính R =$a\sqrt{2}$

C. Tâm là giao điểm hai đường chéo và bán kính R = $\frac{a\sqrt{2}}{2}$

D. Tâm là điểm B và bán kính là R = $\frac{a\sqrt{2}}{2}$

Hiển thị đáp án

Đáp án: C

Giải thích:

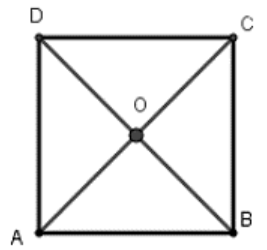
Gọi O là giao hai đường chéo của hình vuông ABCD.

Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2

Xét tam giác vuông tại ta có:

Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là R = $\frac{a\sqrt{2}}{2}$

Câu 25: Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó

A. Tâm là trọng tâm tam giác ABC và bán kính R = 2/3 AI với I là trung điểm của

B. Tâm là trung điểm AB và bán kính R = AB/2

C.Tâm là giao điểm của BD và EC, bán kính là R = AB/2

D. Tâm là trung điểm BC và bán kính là R = BC/2

Hiển thị đáp án

Đáp án: D

Giải thích:

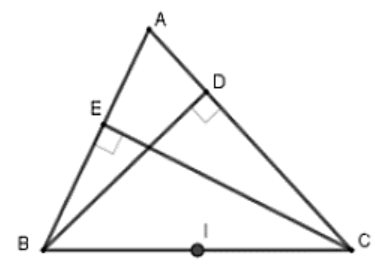
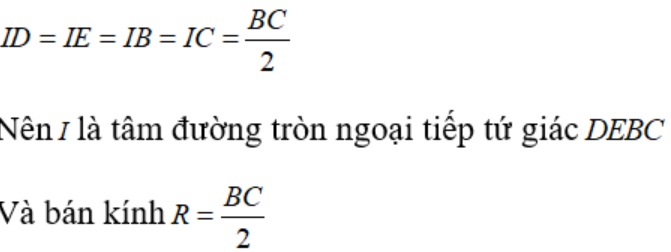
Câu 26: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A(-1; -1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2

A. Điểm A nằm ngoài đường tròn

B. Điểm A nằm trên đường tròn

C. Điểm A nằm trong đường tròn

D. Không kết luận được

Hiển thị đáp án

Đáp án: C

Giải thích:

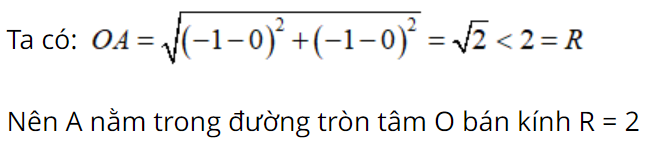
Câu 27: Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC

A. R = 25

B. R = $\frac{25}{2}$

C. R = 15

D. R = 20

Hiển thị đáp án

Đáp án: B

Giải thích:

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính là R = $\frac{BC}{2}$

Theo định lý Pytago ta có: $BC = \sqrt{A{C}^2+A{B}^2} = 25$ nên bán kính R = $\frac{25}{2}$

Câu 28: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D

A. R = 7,5cm

B. R = 13cm

C. R = 6cm

D. R = 6,5cm

Hiển thị đáp án

Đáp án: D

Giải thích:

Gọi I là giao hai đường chéo, ta có IA = IB = IC = ID (vì BD = AC và I là trung điểm mỗi đường)

Nếu bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = $\frac{AC}{2}$

Theo định lý Pytago trong tam giác vuông ABC

Ta có:

$AC = \sqrt{A{B}^2+B{C}^2} = 13$

Nên R = $\frac{AC}{2}$ = 6,5cm

Các câu hỏi trắc nghiệm Toán lớp 9 có đáp án, chọn lọc khác:

40 câu hỏi Trắc nghiệm Căn bậc hai (có đáp án 2022) – Toán 9

40 câu hỏi Trắc nghiệm Căn thức bậc hai và hằng đẳng thức (có đáp án 2022) – Toán 9

40 câu hỏi Trắc nghiệm Liên hệ giữa phép nhân và phép khai phương (có đáp án 2022) – Toán 9

40 câu hỏi Trắc nghiệm Liên hệ giữa phép chia và phép khai phương (có đáp án 2022) – Toán 9

40 câu hỏi Trắc nghiệm Biến đổi đơn giản biểu thức chứa căn thức bậc hai (có đáp án 2022) –Toán 9