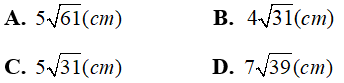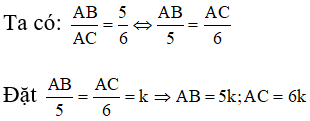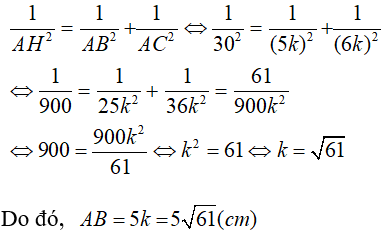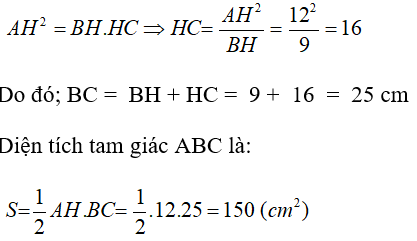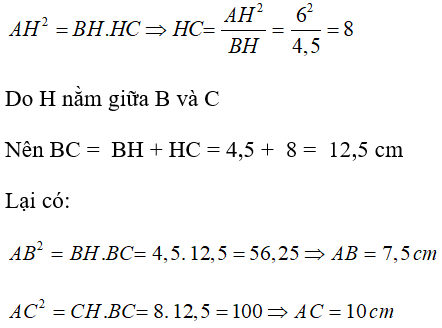TOP 40 câu Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án 2024) – Toán 9
40 câu hỏi trắc nghiệm Toán lớp 9 Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 9
Trắc nghiệm Toán lớp 9 Một số hệ thức về cạnh và đường cao trong tam giác vuông
Bài giảng Trắc nghiệm Toán lớp 9 Một số hệ thức về cạnh và đường cao trong tam giác vuông
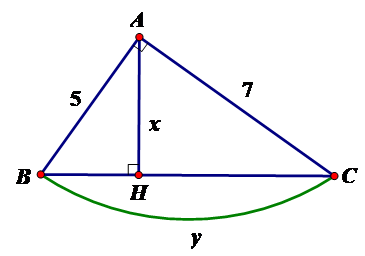
Câu 1: Tìm x, y trong hình vẽ sau:
A. x = 7,2; y = 11,8
B. x = 7; y = 12
C. x = 7,2; y = 12,8
D. x = 7,2; y = 12
Đáp án: C
Giải thích:

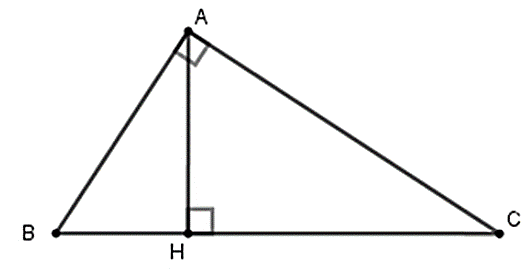
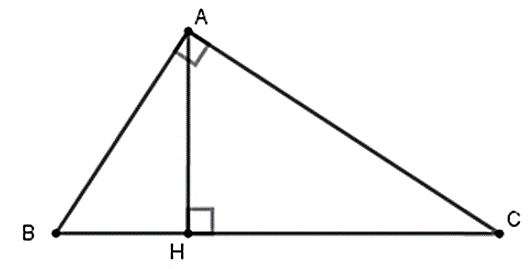
Câu 2: Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
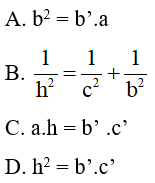
Đáp án: C
Giải thích:
Nhận thấy ah = bc nên phương án C là sai
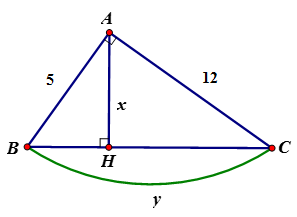
Câu 3: Cho tam giác ABC vuông tại A, chiều cao AH và AB = 5; AC = 12.
Đặt BC = y, AH = x. Tính x, y
A. x = 4; y = √119√119
B. y=6013y=6013; x = 13
C. x = 4; y = 13
D.x=6013x=6013 ; y = 13
Đáp án: D
Giải thích:

Câu 4: Tìm x, y trong hình vẽ sau:
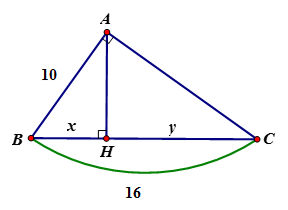
A. x= 6,5; y = 9,5
B. x = 6,25; y = 9,75
C. x = 9,25; y = 6,75
D. x = 6; y = 10
Đáp án: B
Giải thích:
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.BC
⇔BH=AB2BC=10016=6,25⇔BH=AB2BC=10016=6,25
⇒⇒CH = BC – BH = 16 – 6,25 = 9,75
Vậy x = 6,25; y = 9,75
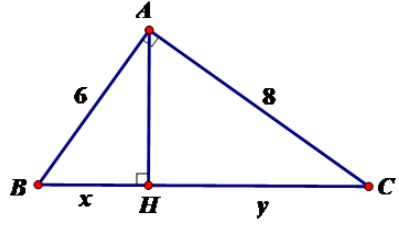
Câu 5: Tính x, y trong hình vẽ sau:
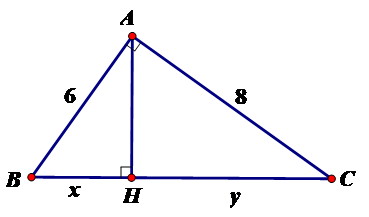
A. x = 3,6; y = 6,4
B. y = 3,6; x = 6,4
C. x = 4; y = 6
D. x = 2,8; y = 7,2
Đáp án: A
Giải thích:
Theo định lý Py-ta-go ta có
BC2 = AB2 + AC2
⇔⇔BC2 = 100 BC = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.BC
⇒BH=AB2BC=6210=3,6⇒BH=AB2BC=6210=3,6 hay x = 3,6
⇒⇒CH = BC – BH = 10 – 3,6 = 6,4
Câu 6: Cho tam giác ABC vuông tại A, AH⊥⊥BC (H thuộc BC).
Cho biết AB : AC = 4 : 5 và BC = √41√41 cm.
Tính độ dài đoạn thẳng CH (làm tròn đến chữ số thập phân thứ nhất).
A. CH≈≈2,5
B. CH≈≈4
C. CH≈≈3,8
D. CH≈≈3,9
Đáp án: D
Giải thích:
Ta có AB : AC = 4 : 5
⇔AB4=AC5⇒AB216=AC225=AB2+AC216+25=4141=1
(Vì theo định lý Py-ta-go ta có
AB2 + AC2 = BC2
⇔ AB2 + AC2 = (√41)2= 41)
Nên AB216=1⇒ AB2 = 16
⇒AB = 4; AC225=1⇒AC = 5
Theo hệ thức lượng trong tam giác vuông ABC ta có:
AC2 = CH.BC
⇒CH=AC2BC=25√41≈3,9
Vậy CH≈3,9
Câu 7: Tính x, y trong hình vẽ sau:
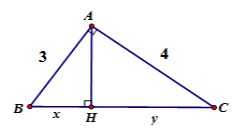
A. x = 3,2; y = 1,8
B. x = 1,8; y = 3,2
C. x = 2; y = 3
D. x = 3; y = 2
Đáp án: B
Giải thích:
Theo định lý Py-ta-go ta có
BC2 = AB2 + AC2
⇔ BC2 = 25 BC = 5
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
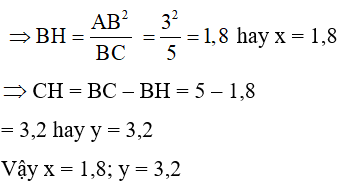
Câu 8: Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
A. 150cm2
B. 300cm2
C. 125cm2
D. 200cm2
Đáp án: A
Giải thích:
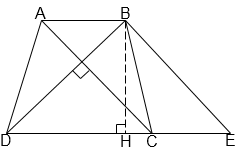
Qua B vẽ đường thẳng song song với AC, cắt DC ở E.
Gọi BH là đường cao của hình thang.
Ta có BE // AC, AC⊥BD nên BE⊥BD
Áp dụng định lý Pytago vào tam giác vuông BDH,
ta có: BH2 + HD2 = BD2
⇒122 + HD2 = 152
⇒ HD2 = 81⇒HD = 9cm
Xét tam giác BDE vuông tại B:
BD2 = DE.DH⇒152 = DE.9
⇒DE = 25cm
Ta có: AB = CE nên:
AB + CD = CE + CD = DE = 25cm
Do đó SABCD = 25.12 : 2 = 150(cm2)
Câu 9: Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?
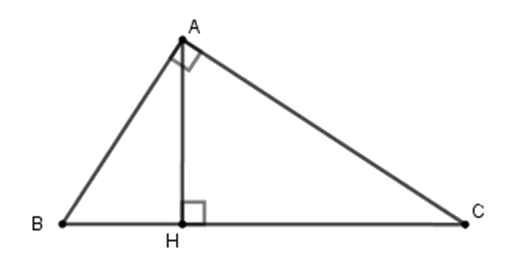
A. AH2 = AB. AC
B. AH2 = BH.CH
C. AH2 = AB.BH
D. AH2 = CH.BC
Đáp án: B
Giải thích:
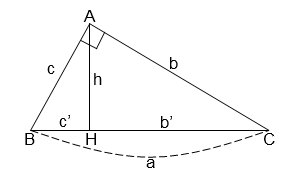
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
HA2 = HB.HC
Câu 10: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21
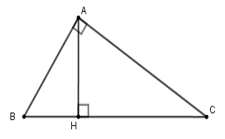
A. AB = 9; AC = 10; BC = 15
B. AB = 9; AC = 12; BC = 15
C. AB = 8; AC = 10; BC = 15
D. AB = 8; AC = 12; BC = 15
Đáp án: B
Giải thích:
Theo giả thiết AB : AC = 3 : 4
Suy ra AB3=AC4=AB+AC3+4=3
Do đó AB = 3.3 = 9 (cm);
AC = 3.4 = 12 (cm)
Tam giác ABC vuông tại A,
theo định lý Pytago ta có:
BC2 = AB2 + AC2 = 92 + 122 = 225,
suy ra BC = 15cm
Câu 11: Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
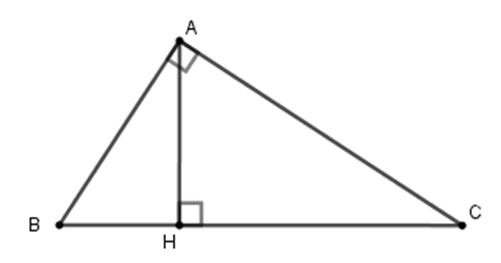
A. AB2 = BH.BC
B. AC2 = CH.BC
C. AB.AC = AH.BC
D. AH2=AB2+AC2AB2.AC2
Đáp án: D
Giải thích:
Cho tam giác ABC vuông tại A,
đường cao AH. Khi đó ta có hệ thức

Câu 12: Cho ABCD là hình thang vuông tại A và D. Đường chép BD vuông góc với BC. Biết AD = 10cm, DC = 20cm. Tính độ dài BC.
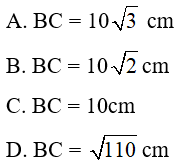
Đáp án: B
Giải thích:
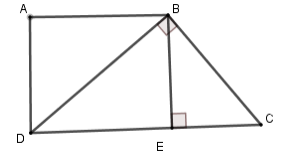


Câu 13: Tính x, y trong hình vẽ sau:
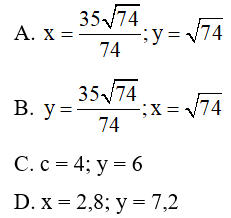
Đáp án: A
Giải thích:

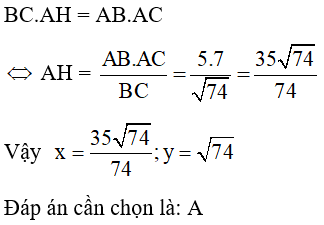
Câu 14: Cho tam giác ABC vuông tại A, AHBC (H thuộc BC). Cho biết AB : AC = 3 : 4 và BC = 15cm. Tính độ dài đoạn thẳng BH
A. Bh = 5,4
B. BH = 4,4
C. BH = 5,2
D. BH = 5
Đáp án: A
Giải thích:
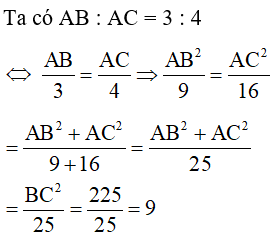
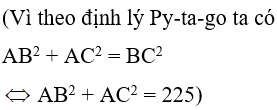
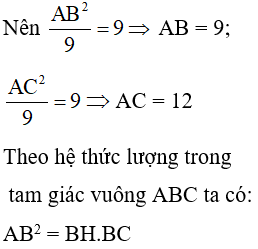
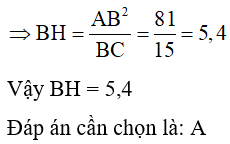
Câu 15: Tìm x trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai).
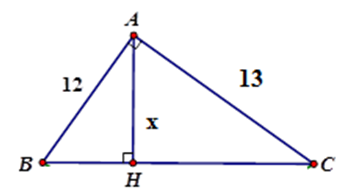
A. x≈8,81
B. x≈8,82
C. x≈ 8,83
D. x≈8,80
Đáp án: B
Giải thích:
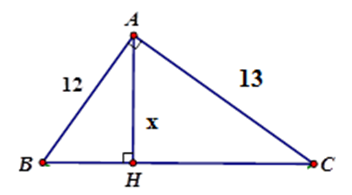
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
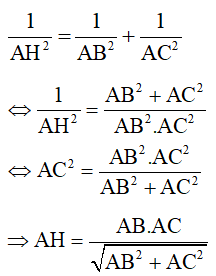
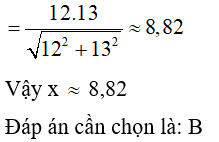
Câu 16: Tính x trong hình vẽ sau:
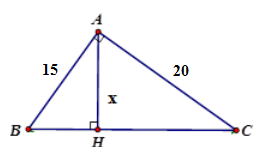
A. x = 14
B. x = 13
C. x = 12
D. x = √145
Đáp án: C
Giải thích:
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
1AH2=1AB2+1AC2⇒AH=AB.AC√AB2+AC2=15.20√152+202=12
Vậy x = 12
Câu 17: “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng…”. Cụm từ thích hợp điền vào chỗ trống là:
A. Tích hai cạnh góc vuông
B. Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
C. Tích cạnh huyền và 1 cạnh góc vuông
D. Tổng nghịch đảo các bình phương của hai cạnh góc vuông.
Đáp án: B
Giải thích:
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
HA2 = HB.HC
Hay “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền”
Câu 18: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 4cm, . Tính chu vi tam giác ABC?
A. 5√5 + 8 cm
B. 6√5 + 12 cm
C. 4√5 + 8 cm
D. 6√5 + 10 cm
Đáp án: D
Giải thích:
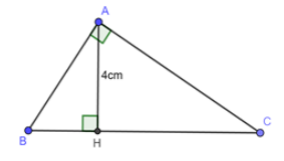
Ta có:HBHC=14 HC = 4HB



Câu 19: Tính x, y trong hình vẽ sau:
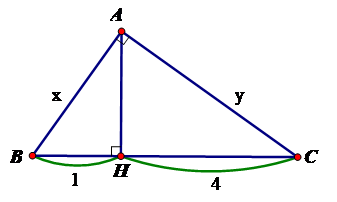
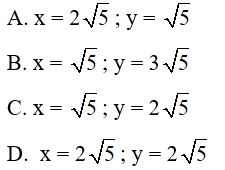
Đáp án: C
Giải thích:


Câu 20: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài các đoạn thẳng CH
A. CH = 96
B. CH = 49
C. CH = 98
D. CH = 89
Đáp án: C
Giải thích:
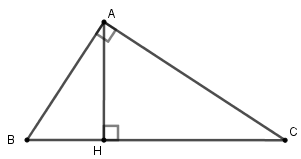
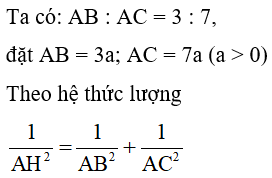
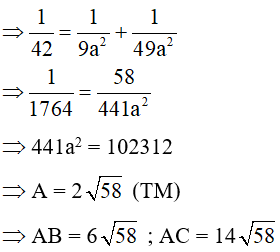

Câu 21: Tính x, y trong hình vẽ sau:
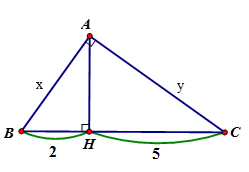
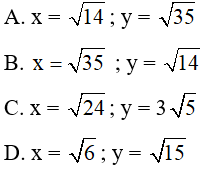
Đáp án: A
Giải thích:
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AH2 = BH.CH
⇒AH2 = 2.5⇒AH =√10
Áp dụng định lý Pytago cho tam giác vuông AHB, AHC ta có
AB =√AH2+HB2=√10+4=√14 ;
AC =√AH2+HC2=√10+25=√35
Vậy x = √14; y =√15
Câu 22: Tính x trong hình vẽ sau:
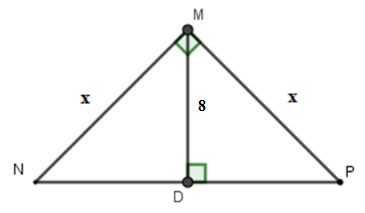
A. x = 6√2
B. x = 8√2
C. x = 8√3
D. x = 8√2
Đáp án: B
Giải thích:

Câu 23: Cho tam giác ABC vuông tại A. BiếtABAC=37 , đường cao AH = 42cm. Tính BH, HC
A. BH = 18cm; HC = 98cm
B. BH = 24cml HC = 72cm
C. BH = 20cm; HB = 78cm
D. BH = 28cm; HC = 82cm
Đáp án: A
Giải thích:



Câu 24: Cho ABCD là hình tháng vuông A và D. Đường chéo BD vuông góc với BC. Biết AD = 12cm, DC = 25cm. Tính độ dài BC, biết BC < 20
A. BC = 15cm
B. BC = 16cm
C. BC = 14cm
D. BC = 17cm
Đáp án: A
Giải thích:
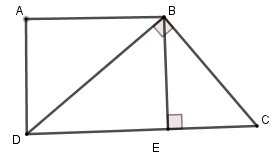


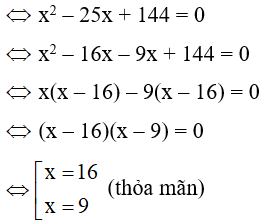

Câu 25: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
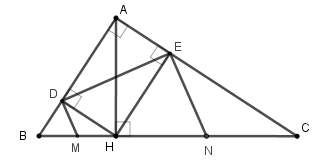
Tính độ dài đoạn thẳng DE.
A. DE = 12cm
B. DE = 8cm
C. DE = 15cm
D. DE = 6cm
Đáp án: A
Giải thích:

Nên DE = 12cm
Câu 26: Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh huyền là 125cm. Tính độ dài các cạnh của tam giác vuông đã cho?
A. 50 và 75
B. 25 và 75
C. 75 và 100
D.60 và 80
Đáp án: C
Giải thích:
Gọi tam giác vuông đã cho là tam giác ABC vuông tại A; AB < AC và đường cao AH.

Do đó. AB = 3.25 = 75cm và AC = 4.25= 100cm
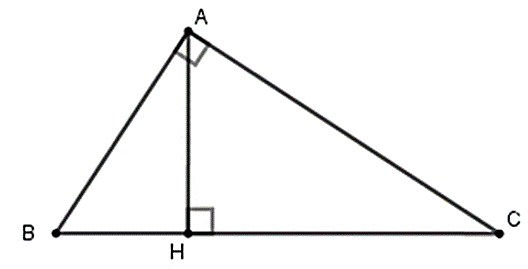
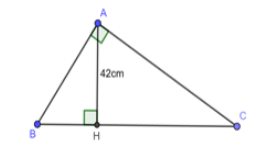
Câu 27: Cho tam giác ABC vuông tại A. Biết 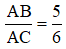
Đáp án: A
Giải thích:
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Câu 28: Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC biết AH = 12 cm; BH = 9cm.
A. 100 cm2
B. 150 cm2
C. 125 cm2
D. 200 cm2
Đáp án: B
Giải thích:
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Câu 29: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 6cm; BH = 4,5 cm.
Tìm khẳng định đúng trong các khẳng định sau ?
A. AB = 10
B. AC = 7,5
C. BC= 12, 5
D. HC = 9
Đáp án: C
Giải thích:
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
BC2 = AC2 + AB2 = 7.52+102= 156.25 ⇒BC= 12.5cm
Câu 30: Tính x, y trong hình vẽ sau:
A. x = 3,6; y = 6,4
B. y = 3,6; x = 6,4
C. x = 4; y = 6
D. x = 2; y = 7,2
Đáp án: A
Giải thích:
Theo định lý Pytago ta có:
BC2 = AB2 + AC2 ⇔ BC2 = 100 ⇔ BC = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 3,6; y = 6,4
Câu 31: Tính x, y trong hình vẽ sau:
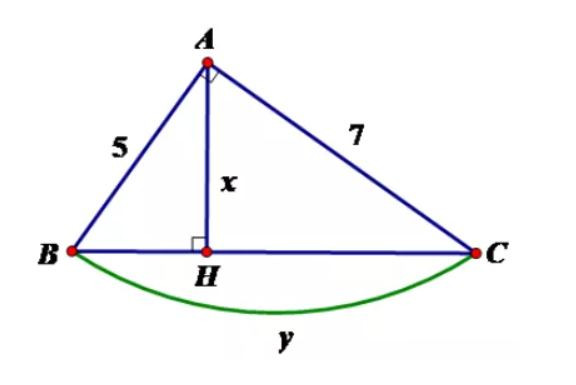
A. x = 35√7474; y = √74
B. y = 35√7474; x = √74
C. x = 4; y = 6
D. x = 2.8; y = 7.2
Đáp án: A
Giải thích:

Câu 32: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm; CH = 16cm.
Tìm khẳng định sai trong các khẳng định sau:
A. AH = 15cm
B. AB = 12cm
C. AC = 20cm
D. AH = 12cm
Đáp án: A
Giải thích:
Ta có: BC = BH + HC = 9 + 16 = 25
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
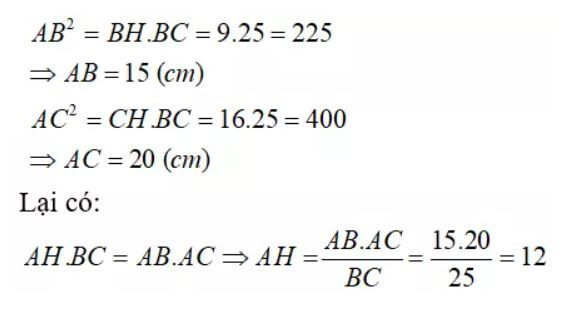
Câu 33: Cho tam giác ABC vuông tại A, biết ABAC = 23, đường cao AH = 6cm. Tính các cạnh của tam giác.
A. AB = 4cm; AC = 6cm; BC = 2√13cm
B. AB = 2cm; AC = 3cm; BC = √13cm
C. AB = 2√15cm; AC = 3√15cm; BC = 5√15cm
D. AB = 2√13cm; AC = 3√13cm; BC = 13cm
Đáp án: D
Giải thích:

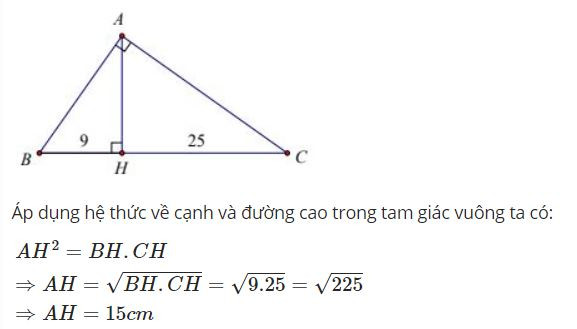
Câu 34: Cho tam giác ABC vuông tại A, đường cao AH, biết BH = 9cm, CH = 25cm. Tính AH.
A. AH = 15cm
B AH = 18cm
C. AH = 10cm
D. AH = 12cm
Đáp án: A
Giải thích:
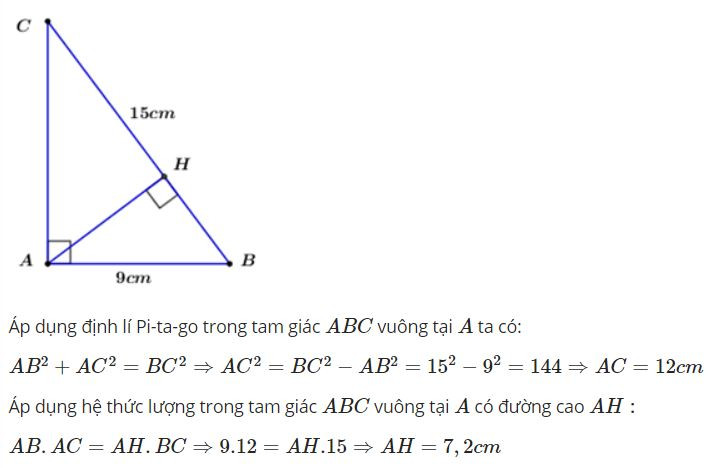
Câu 35: Cho tam giác ABC vuông tại A, đường cao AB = 9cm, BC = 15cm. Khi đó độ dài AH bằng:
A. 6.5cm
B. 7.2cm
C. 7.5cm
D. 7.7cm
Đáp án: B
Giải thích:
Các câu hỏi trắc nghiệm Toán lớp 9 có đáp án, chọn lọc khác:
Trắc nghiệm Tỉ số lượng giác của góc nhọn và Bảng lượng giác có đáp án - Toán 9
Trắc nghiệm Một số hệ thức về cạnh và góc trong tam giác vuông có đáp án – Toán 9
Trắc nghiệm Ôn tập chương 1 Hình học có đáp án – Toán 9
Trắc nghiệm Sự xác định đường tròn. Tính chất đối xứng của đường tròn có đáp án– Toán 9
Trắc nghiệm Đường kính và dây của đường tròn có đáp án– Toán 9
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án