25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P2)

Câu 1:

17/07/2024

Cho hai điểm A(2; 2); B( 5; -2) . Tìm M trên tia Ox sao cho $\hat{A M B} = 90^{o}$

A. M(1; 4)

B. (0; 6)

C. M(1;0) hoặc M(6; 0)

D. M(0;1)

Xem đáp án

Chọn C.

Gọi M(x; 0).

Khi đó .

Theo đàu bài suy ra AM và MB vuông góc với nhau

ta có

nên : (x - 2) (x - 5) – 4 = 0 hay x²- 7x + 6 = 0 $(x - 1) (x - 6) = 0 \Leftrightarrow [\begin{matrix} x - 1 = 0 \\ x - 6 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 1 \\ x = 6 \end{matrix}$

suy ra: x = 1; y = 0 hoặc x = 6; y = 0.

Câu 2:

17/07/2024

Trong mặt phẳng tọa độ Oxy cho hai vectơ $\vec{u} = \vec{i} + 2 \vec{j}; \vec{v} = k \vec{i} + 2 \vec{j}$ . Tìm k để vectơ $\vec{u}$ vuông góc với vectơ $\vec{v}$

A. k = 2

B. k = 8

C. k = -4

D. k = 4

Xem đáp án

Chọn C.

Từ giả thiết suy ra

Để 2 vecto trê vuông góc với nhau khi và chỉ khi:

nên 1.k + 2.2 = 0

Do đó: k = -4

Câu 3:

18/07/2024

Cho tam giác ABC có BC = a; CA = b; AB = c. Tính $\vec{A B} . \vec{A C}$

A. ½.( c²+ b²- a²)

B. c²+ b²- a²

C. a²- b²- c²

D. a²+ b²+ c²

Xem đáp án

Chọn A.

Ta có

Câu 4:

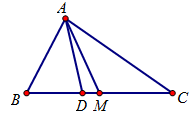
20/07/2024

Cho tam giác ABC có BC = a; CA = b; AB = c. M là trung điểm của BC, D là chân đường phân giác trong góc A. Tính ${\vec{A M}}^{2}$

A.

B.

C.

D.

Xem đáp án

Chọn A.

+ Vì M là trung điểm của BC nên

Suy ra

Theo câu trên ta có nên

Câu 5:

21/07/2024

Cho các vectơ $\vec{a}; \vec{b}$ có độ dài bằng 1 và thoả mãn điều kiện $2 \vec{a} - 3 \vec{b} = \sqrt{7}$ . Tính cos $(\vec{a}; \vec{b})$

A. 1

B. 0

C. 0,5

D. Tất cả sai

Xem đáp án

Chọn C.

Do nên

Hay nên

Mà nên

Câu 6:

09/10/2024

Cho các véctơ $\vec{a}; \vec{b}$ có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 60⁰. Xác định cosin góc giữa hai vectơ $\vec{u} = \vec{a} + 2 \vec{b}; \vec{v} = \vec{a} - \vec{b}$

A. -1/2

B. -1/4

C. -1/6

D. 0

Xem đáp án

Đáp án đúng: C.

*Phương pháp giải:

- Tính tích của 2 vecto: $\vec{u} . \vec{v}$

- Tính độ dài của từng vecto

- Áp dụng công thức tính góc giữa 2 vecto dể tính ra cosin

*Lời giải:

Ta có:

Mặt khác : nên

nên

Suy ra

* Các dạng bài tập và lý thuyết thêm

a) Tích vô hướng của hai vectơ

Trong không gian Oxyz, tích vô hướng của hai vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ được xác định bởi công thức:

$\vec{a} . \vec{b} = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$

b) Ứng dụng của tích vô hướng

+ Cho vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ , khi đó độ dài của vectơ $\vec{a}$ được tính theo công thức:

$|\vec{a}| = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{2}^{2}}$

+ Cho hai điểm $A (x_{A}; y_{A}; z_{A})$ và $B (x_{B}; y_{B}; z_{B})$ . Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ $\vec{A B}$ . Do đó ta có

+ Cho vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Khi đó góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ được tính theo công thức:

$\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}}{\sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2} + b_{3}^{2}}}$

(với $\vec{a}, \vec{b} \neq \vec{0}$ )

+ Hai vectơ vuông góc: Cho vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Khi đó:

$\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} = 0$

2. Tích có hướng của hai vectơ

a) Tích có hướng của hai vectơ

Trong không gian Oxyz cho hai vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ , $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Tích có hướng của hai vectơ $\vec{a}$ và $\vec{b},$ kí hiệu là $[\vec{a}, \vec{b}]$ , được xác định bởi

$[\vec{a}, \vec{b}] = (|\begin{matrix} a_{2} & a_{3} \\ b_{2} & b_{3} \end{matrix}|; |\begin{matrix} a_{3} & a_{1} \\ b_{3} & b_{1} \end{matrix}|; |\begin{matrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{matrix}|) = (a_{2} b_{3} - a_{3} b_{2}; a_{3} b_{1} - a_{1} b_{3}; a_{1} b_{2} - a_{2} b_{1})$

Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

3. Ứng dụng của tích có hướng

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Tích của vectơ với một số có đáp án (Nhận biết)

Bài toán về tích vô hướng và tích có hướng của hai vectơ (có đáp án)

75 câu trắc nghiệm Vectơ nâng cao

Câu 7:

17/07/2024

Giá trị của E = sin36⁰.cos6⁰ - sin126⁰.cos84⁰ là

A. 0,5

C. 1

D. -1

Xem đáp án

Chọn A.

Ta có:

E = sin36⁰.cos6⁰ - sin126⁰.cos84⁰= sin36⁰.cos6⁰- sin(90⁰+ 36⁰).cos(90⁰ - 6⁰)

E = sin36⁰.cos6⁰- cos36⁰.sin6⁰= sin30⁰= 0,5

Câu 8:

19/07/2024

Giá trị của biểu thức A = sin²41⁰+ sin²45⁰+ sin²49⁰+ sin²45⁰ là

A. 3.

B. 4.

C. 1.

D. 2.

Xem đáp án

Chọn D.

Ta có:

A = sin²41⁰+ sin²45⁰+ sin²49⁰+ sin²45⁰= (sin²41⁰+ sin²49⁰)+( sin²45⁰+ sin²45⁰)

A = (sin²41⁰+ cos²49⁰) + ( sin²45⁰+ cos²45⁰) = 1 + 1 = 2.

Câu 9:

22/09/2024

Cho biết cosα = -2/3 . Tính giá trị của biểu thức ? $E = \frac{c o t α + 3 \tan α}{2 c o t α + \tan α}$ ?

A. $- \frac{19}{13}$

B. $\frac{19}{13}$

C. $\frac{25}{13}$

D. - $\frac{19}{3}$

Xem đáp án

Chọn B.

Nhân cả tử và mẫu với tanα ta được

\

* Một số công thức cần nhớ để áp dụng

1. Công thức cộng

$\begin{array}{l} \sin (a + b) = \sin a \cos b + \cos a s i n b \\ s i n (a - b) = \sin a \cos b - \cos a s i n b \\ \cos (a + b) = \cos a \cos b - \sin a s i n b \\ \cos (a - b) = \cos a \cos b + \sin a s i n b \\ \tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b} \\ \tan (a - b) = \frac{\tan a - \tan b}{1 + \tan a \tan b} \end{array}$

2. Công thức nhân đôi

$\begin{array}{l} \sin 2 a = 2 \sin a \cos a \\ \cos 2 a = \cos^{2} a - \sin^{2} a = 2 \cos^{2} a - 1 = 1 - 2 \sin^{2} a \\ \tan 2 a = \frac{2 \tan a}{1 - \tan^{2} a} \end{array}$

Suy ra, công thức hạ bậc:

$\sin^{2} a = \frac{1 - \cos 2 a}{2}, \cos^{2} a = \frac{1 + \cos 2 a}{2}$

3. Công thức biến đổi tích thành tổng

$\begin{array}{l} \cos a \cos b = \frac{1}{2} [\cos (a + b) + \cos (a - b)] \\ \sin a \sin b = \frac{1}{2} [\cos (a - b) - \cos (a + b)] \\ \sin a \cos b = \frac{1}{2} [\sin (a + b) + \sin (a - b)] \end{array}$

4. Công thức biến đổi tổng thành tích

$\begin{array}{l} \cos a + \cos b = 2 \cos \frac{a + b}{2} \cos \frac{a - b}{2} \\ \cos a - \cos b = - 2 \sin \frac{a + b}{2} \sin \frac{a - b}{2} \\ \sin a + \sin b = 2 \sin \frac{a + b}{2} \cos \frac{a - b}{2} \\ \sin a - \sin b = 2 \cos \frac{a + b}{2} \sin \frac{a - b}{2} \end{array}$

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Bài giảng Toán 11 Bài 2: Công thức lượng giác

Giải Toán 11 Bài 2: Công thức lượng giác

Câu 10:

17/07/2024

Cho biết cotα = 5. Tính giá trị của E = 2 cos²α + 5sinα.cosα + 1?

Xem đáp án

Chọn D.

Ta có:

Câu 11:

20/07/2024

Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy điểm N sao cho DN = 1 và P là trung điểm BC. Tính cosMNP?

Xem đáp án

Chọn C.

Ta có

Suy ra

Mặt khác

Câu 12:

17/07/2024

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB = CD = 2a; $M N = a \sqrt{3}$ .

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Xem đáp án

Chọn C.

Ta có: suy ra

Do đó

Câu 13:

12/07/2024

Tính A = sin²2⁰ + sin²4⁰+ sin² 6⁰+… + sin²84⁰+ sin²86⁰+ sin²88⁰.

A. 20

B. 22

C. 24

D. 23

Xem đáp án

Chọn B.

Ta có: A = sin²2⁰ + sin²4⁰+ sin² 6⁰+…+ sin²84⁰+ sin²86⁰+ sin²88⁰

A = ( sin²2⁰ + sin² 88⁰) + ( sin² 4⁰+ sin²86⁰) +...+ (sin²44⁰+ sin²46⁰)

A = ( sin²2⁰ + cos²2⁰) + ( sin² 4⁰+…+ cos²4⁰) +...+ ( sin²44⁰+ cos²44⁰) ( do 2 góc phụ nhau sin góc này bằng cos góc kia).

A = 1 + 1 + 1 + ... + 1 = 22

Câu 14:

23/07/2024

Biết sina+ cosa = $\sqrt{2}$ . Hỏi giá trị của sin⁴a + cos⁴a bằng bao nhiêu?

A. 1

B. 0,5

C. -1

D. 0

Xem đáp án

Chọn B.

Ta có:

Nên (sina + cosa)²=2 hay sin²a + cos²a + 2 sina.cosa = 2

Suy ra sina.cosa = ½.

Khi đó: sin⁴a + cos⁴a = (sin²a + cos²a)²- 2sin²a.cos²a = 1 - 2.(1/2)²= ½.

Câu 15:

20/07/2024

Biểu thức A = 3(sin⁴x + cos⁴x) - 2 (sin⁶x + cos⁶x) có giá trị bằng:

A. 1

B. 2

C. -1

D. 0

Xem đáp án

Chọn A.

Ta có:

+ sin⁴x + cos⁴x = (sin²x + cos²x)²- 2sin²x.cos²x = 1 - 2sin²x.cos²x.

+ sin⁴x + cos⁴x = 1 - 3sin²x.cos²x.

Do đó

A = 3(1 - 2sin²x^.cos²x) - 2(1 - 3sin²x.cos²x) = 1.

Câu 16:

23/07/2024

Biểu thức: A = cos⁴x + cos²x sin²x + sin²x có giá trị bằng

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn A.

Từ giả thiết suy ra:

A = (cos⁴x + cos²x sin²x) + sin²x = cos²x(sin²x + cos²x ) + sin²x

A = cos²x.1 + sin²x = 1

Câu 17:

07/11/2024

Biểu thức B = sin²x.tan²x – tan²x + sin² x có giá trị bằng

A. -2

B. -1

C. 0

D. 1

Xem đáp án

Đáp án đúng: C.

*Lời giải:

Từ giả thiết ta suy ra:

B = tan²x (sin²x - 1) + sin² x = -tan²x.cos²x + sin²x

*Phương pháp giải:

- áp dụng các công thức lượng giác để biến đổi rồi thực hiện phép tính tìm ra kết quả

*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:

Công thức nhân đôi:

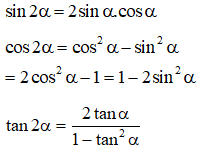
* Công thức hạ bậc:

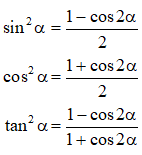
Phương trình cosx=a

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $|cosx| \leq 1$ với mọi x.

- Trường hợp $|a| \leq 1$ .

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x = \pm α + k 2 π; k \in ℤ$

Phương trình tanx=a

- Điều kiện xác định của phương trình là $x \neq \frac{π}{2} + k π; k \in ℤ$

Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là: $x = \arctan a + k π; k \in ℤ$

+) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là: $x = α + k π; k \in ℤ$

Tổng quát; tan f(x) = tan g(x) $\Rightarrow f (x) = g (x) + k π; k \in ℤ$ .

+) Phương trình tanx = tanβ⁰ có các nghiệm là: $x = β^{0} + k {.180}^{0}; k \in ℤ$ .

Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.

Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết $f (x) = 0 \Leftrightarrow g (x) = 0$

*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:

at + b = 0 (1)

Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.

- Phương pháp:

Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.

Phương trình bậc hai với hàm số lượng giác

Định nghĩa.

Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:

at² + bt + c = 0

Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Phương trình lượng giác cơ bản – Toán 11

Bài tập Phương trình lượng giác cơ bản Toán 11

Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án)– Toán 11

Câu 18:

21/07/2024

Cho cotα = 1/3. Giá trị của biểu thức là:

A. -11

B. 11

C. 12

D. 13

Xem đáp án

Chọn D.

Ta có: cosα = sinα.cotα nên từ giả thiết suy ra:

Câu 19:

19/07/2024

Cho biết cosα = -2/3. Giá trị của biểu thức $E = \frac{c o t α - 3 \tan α}{2 c o t α - \tan α}$ bằng bao nhiêu?

A . $\frac{- 25}{3}$

B. $\frac{11}{3}$

C. - $\frac{11}{3}$

D. $\frac{16}{3}$

Xem đáp án

Chọn C.

Nhân cả tử và mẫu với tanα và chú ý tanα.cotα = 1 ta được:

Câu 20:

18/07/2024

Cho tanα + cotα = m. Tìm m để tan²α + cot²α = 7.

A. m = 3

B. m = 6

C. m = -3

D. m = ± 3

Xem đáp án

Chọn D.

Theo giả thiết tan²α + cot²α = 7.

Nên ( tanα + cotα) ²= tan²α + cot²α + 2tanα.cotα = 7 + 2 = 9

Suy ra: tanα + cotα = 3 hoặc tanα + cotα = -3

Suy ra: m = 3 hoặc m = -3.

Câu 21:

09/11/2024

Biểu thức (cota + tana)²bằng

A.

B. cot²a + tan²a.

C .

D. cot²a.tan²a + 2.

Xem đáp án

Đáp án đúng là :C.

Lời giải

Ta có: cota + tana) ²= cot²a + 2.cota.tana + tan²a

= (cot²a + 1) + (tan²a + 1)

*Phương pháp giải:

Nhớ được công thức lượng giác cơ bản

*Lý thuyết

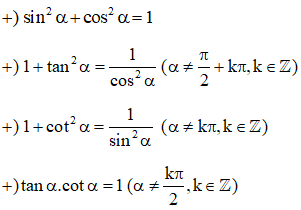
Xem thêm

Lý thuyết Phương trình lượng giác cơ bản (mới + Bài Tập) – Toán 11

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án ) – Toán 11

Câu 22:

10/11/2024

Đơn giản biểu thức $E = c o t x + \frac{\sin x}{1 + \cos x}$ ta được

A. sinx

B.

C.

D. tanx

Xem đáp án

Đáp án đúng là C.

Lời giải

Ta có:

*Phương pháp giải:

Sử dụng công thức chu kì và hai góc phụ nhau, bù nhaun để tính giá trị của biểu thức.

*Lý thuyết:

Đối với hai góc bù nhau, α và 180° – α, ta có:

sin (180° – α) = sin α;

cos (180° – α) = - cos α;

tan (180° – α) = - tan α (α ≠ 90°);

cot (180° – α) = - cot α (0° < α < 180°).

Chú ý:

- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.

Xem thêm

Tổng hợp lý thuyết Chương 3 – Toán 10 Kết nối tri thức

TOP 30 câu Trắc nghiệm Ôn tập chương 7 (Cánh diều 2024) có đáp án - Toán 7

Câu 23:

17/07/2024

Rút gọn biểu thức sau $A = \frac{c o t^{2} x - \cos^{2} x}{c o t^{2} x} + \frac{\sin x . \cos x}{c o t x}$

A. A = 1

B. A = -1

C. A = -2

D. A = 2

Xem đáp án

Chọn A.

Ta có:

Câu 24:

23/07/2024

Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?

A.

B.

C.

D.

Xem đáp án

Chọn C.

+ Phương án A: ABCD là hình vuông nên OA và OB vuông góc với nhau

suy ra $\vec{O A} . \vec{O B} = 0$ loại A.

+ Phương án B: OA và OC vuông góc với nhau nên $\vec{O A} . \vec{O C} = 0$ và $\frac{1}{2} \vec{O A} . \vec{A C} = 0$

suy ra $\vec{O A} . \vec{O C} = \frac{1}{2} \vec{O A} . \vec{A C} = 0$ loại B.

+ Phương án C: $\vec{A B} . \vec{A C} = A B . A C . \cos 45 ° = A B . A B . \sqrt{2} . \frac{\sqrt{2}}{2} = A B^{2}$

Do $\vec{A B}, \vec{C D}$ là hai vecto ngược hướng nên $(\vec{A B}; \vec{C D}) = 180 °$

suy ra :

Câu 25:

18/07/2024

Trong mặt phẳng tọa độ Oxy cho các điểm A(1;2); B(-2; -4) và C(0;1); D(-1; 3/2). Mệnh đề nào sau đây đúng ?

A. $\vec{A B} c ù n g p h ư ơ n g v ớ i \vec{C D}$

B.

C.

D.

Xem đáp án

Chọn C.

Ta có và

suy ra

Vậy 2 vecto đó vuông góc với nhau.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3