25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P1)

Câu 1:

01/11/2024

Cho tam giác ABC thoả mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng ?

A. cosB + cosC = 2cos A

B. sinB + sinC = 2sinA

C. sin C = cosA + sin B

D. sinB + cosA = cosC

Xem đáp án

Đáp án đúng: B.

*Lời giải

Ta có:

Hay sinB + sin C = 2sinA

*Phương pháp giải

- Áp dụng định lý sin trong tam giác. Thay b+ c= 2a vào để tính toán

*Lý thuyến cần nắm về tích vô hướng của hai vectơ:

Góc giữa hai vectơ

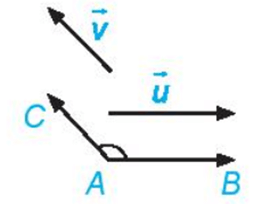
Cho hai vectơ $\vec{u}$ và $\vec{v}$ khác $\vec{0}$ . Từ một điểm A tùy ý, vẽ các vectơ $\vec{A B} = \vec{u}$ và $\vec{A C} = \vec{v}$ . Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ $\vec{u}$ và $\vec{v}$ hay đơn giản là góc giữa hai vectơ $\vec{u}$ , $\vec{v}$ , kí hiệu là ( $\vec{u}$ , $\vec{v}$ ).

Chú ý :

+ Quy ước rằng góc giữa hai vectơ $\vec{u}$ và $\vec{0}$ có thể nhận một giá trị tùy ý từ 0° đến 180°.

+ Nếu ( $\vec{u}$ , $\vec{v}$ ) = 90° thì ta nói rằng $\vec{u}$ và $\vec{v}$ vuông góc với nhau. Kí hiệu $\vec{u}$ ⊥ $\vec{v}$ hoặc $\vec{v}$ ⊥ $\vec{u}$ . Đặc biệt được coi là vuông góc với mọi vectơ.

Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không $\vec{u}$ và $\vec{v}$ là một số, kí hiệu là $\vec{u}$ . $\vec{v}$ , được xác định bởi công thức sau:

$\vec{u}$ . $\vec{v}$ = | $\vec{u}$ |.| $\vec{v}$ |.cos( $\vec{u}$ , $\vec{v}$ )

Chú ý:

+) $\vec{u}$ ⊥ $\vec{v}$ ⇔ $\vec{u}$ . $\vec{v}$ = 0.

+) $\vec{u}$ . $\vec{u}$ còn được viết là ${\vec{u}}^{2}$ và được gọi là bình phương vô hướng của vectơ $\vec{u}$ .

Ta có ${\vec{u}}^{2} = | \vec{u} | . | \vec{u} | . \cos 0 ° = {(\vec{u})}^{2}$ .

(Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.)

Biểu thức tọa độ và tính chất của tích vô hướng

Tích vô hướng của hai vectơ $\vec{u} = (x; y)$ và $\vec{v} = (x'; y')$ được tính theo công thức :

$\vec{u}$ . $\vec{v}$ = x.x' + y.y'.

Nhận xét:

+ Hai vectơ $\vec{u}$ và $\vec{v}$ vuông góc với nhau khi và chỉ khi x.x' + y.y' = 0.

+ Bình phương vô hướng của $\vec{u} = (x; y)$ là ${\vec{u}}^{2}$ = x2 + y2.

+ Nếu $\vec{u}$ ≠ $\vec{0}$ và $\vec{v}$ ≠ $\vec{0}$ thì cos( $\vec{u}$ , $\vec{v}$ ) = $\frac{\vec{u} . \vec{v}}{| \vec{u} | . | \vec{v} |} = \frac{x x' + y y'}{\sqrt{x^{2} + y^{2}} . \sqrt{x'^{2} + y'^{2}}}$ .

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Tích vô hướng của hai vectơ - Toán 10 Kết nối tri thức

Giải Toán 10 Bài 11 (Kết nối tri thức): Tích vô hướng của hai vecto

Câu 2:

22/07/2024

Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Câu nào sau đây sai?

A. $\vec{A B} . \vec{D C} = 8 a^{2}$

B. $\vec{A D} . \vec{C D} = 0$

C. $\vec{A D} . \vec{A B} = 0$

D. $\vec{D A} . \vec{D B} = 0$

Xem đáp án

Chọn D.

Phương án A: = AB.DC.cos0⁰

= 8a² nên loại A.

Phương án B: suy ra nên loại B.

Phương án C: suy ra nên loại C.

Phương án D: không vuông góc với suy ra nên chọn D.

Câu 3:

14/07/2024

Cho 2 vec tơ $\vec{a} (a_{1}; a_{2}); v à \vec{b} (b_{1}; b_{2})$ . Biểu thức sai là:

A.

B.

C.

D.

Xem đáp án

Chọn C.

Phương án A : biểu thức tọa độ tích vô hướng nên loại A.

Phương án B : Công thức tích vô hướng của hai véc tơ nên loại B.

Phương án C: nên chọn C.

Câu 4:

27/11/2024

Cho tam giác ABC. Đẳng thức nào sai ?

A. sin( A + B - 2C) = sin3C

B.

C. sin( A + B) = sinC

D.

Xem đáp án

Đáp án đúng: D.

*Lời giải:

Ta có: A + B + C = 180⁰

*Phương pháp giải:

- Nắm vững lý thuyết và tính chất của tích vô hướng hai vectơ: góc giữa hai vectơ, tính chất và ứng dụng tích vô hướng

*Một số lý thuyết và dạng bài tập về vectơ:

- Định nghĩa góc giữa hai vectơ: Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $\vec{0}$ . Từ điểm O bất kì vẽ $\vec{O A} = \vec{a}$ , $\vec{O B} = \vec{b}$ , khi đó góc $\hat{A O B}$ ( $0^{o} \leq \hat{A O B} \leq 180^{o}$ ) là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ . Kí hiệu: $(\vec{a}, \vec{b})$ .

- Định nghĩa tích vô hướng: Cho hai vectơ $\vec{a}$ và $\vec{b}$ ( $\vec{a}, \vec{b} \neq \vec{0}$ ), khi đó tích vô hướng của $\vec{a}$ và $\vec{b}$ kí hiệu là $\vec{a} . \vec{b}$ và xác định bởi công thức: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ .

Chú ý:

+) Khi ít nhất một trong hai vectơ $\vec{a}$ và $\vec{b}$ bằng vectơ $\vec{0}$ ta quy ước: $\vec{a} . \vec{b} = 0$ .

+) Với hai vectơ $\vec{a}$ và $\vec{b}$ (), ta có: $\vec{a} . \vec{b} = 0 \Leftrightarrow \vec{a} ⊥ \vec{b}$ .

+) Tích vô hướng $\vec{a} . \vec{a}$ được kí hiệu là ${\vec{a}}^{2}$ và ta có: ${\vec{a}}^{2} = {|\vec{a}|}^{2}$ .

- Ứng dụng của tích vô hướng:

+) Độ dài của vectơ $\vec{a} = (a_{1}; a_{2})$ được tính theo công thức: $|\vec{a}| = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}}$

+) Góc giữa hai vectơ $\vec{a} = (a_{1}; a_{2})$ và $\vec{b} = (b_{1}; b_{2})$ ( $\vec{a}; \vec{b} \neq \vec{0}$ ):

$\cos (\vec{a}; \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{a_{1}^{2} + a_{2}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2}}}$

+) Khoảng cách giữa hai điểm $A (x_{A}; y_{A})$ và $B (x_{B}; y_{B})$ được tính theo công thức:

$A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$

Xem thêm các bài viết liên quan hay, chi tiết

Trắc nghiệm Tích vô hướng của hai vecto có đáp án – Toán lớp 10

Chứng minh đẳng thức về tích vô hướng của vectơ hoặc về độ dài đoạn thẳng

Câu 5:

12/07/2024

Cho A(2; 5); B(1; 3) và C(5; -1). Tìm tọa độ điểm K sao cho

A. (-4; -4).

B. (-4; 5).

C. (5; -4).

D. (-5; -4).

Xem đáp án

Chọn B.

Gọi K(x; y).

Khi đó

Theo đầu bài nên

Câu 6:

22/07/2024

Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC. Tính $\vec{A H} . \vec{C A}$

A. $\frac{3 a^{2}}{4}$

B. - $\frac{3 a^{2}}{4}$

C. $\frac{3 a^{2}}{2}$

D. - $\frac{3 a^{2}}{2}$

Xem đáp án

Chọn B.

Ta có:

Do đó:

Câu 7:

22/07/2024

Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai?

Xem đáp án

Chọn C.

Ta có :

Ta đi xét các phương án:

Phương án A: nên

Loại A.

Phương án B:

Loại B.

Phương án C:

Chọn C.

Câu 8:

17/07/2024

Cho tam giác ABC là tam giác đều. Mệnh đề nào sau đây đúng?

A.

B.

C.

D.

Xem đáp án

Chọn D.

+ Phương án A: Do

Loại A.

+ Phương án B: và nên

Loại B.

+ Phương án C: Do và không cùng phương.

Loại C.

+ Phương án D: AB = BC = CA

Câu 9:

28/11/2024

Tam giác ABC có a = 6; $b = 4 \sqrt{2}$ ; c = 2; gọi M là điểm trên cạnh BC sao cho BM = 3 . Độ dài đoạn AM bằng bao nhiêu ?

A. 5

B. 9

C. 3

D. 6

Xem đáp án

Đáp án đúng là C.

Lời giải

Trong tam giác ABC có a = 6 nên BC = 6 mà BM = 3

suy ra M là trung điểm BC

Suy ra:

*Phương pháp giải:

- Áp dụng công thức độ dài đường trung tuyến AM trong tam giác ABC để tính ra AM

Lý thuyết

Định lí côsin

Cho tam giác ABC có BC = a, AC = b và AB = c. Ta có

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

Hệ quả

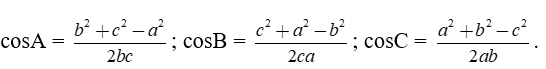
Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án

Định lí sin

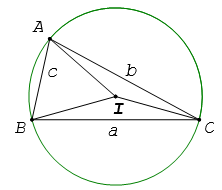
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.

Ta có

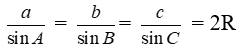
Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án

Độ dài đường trung tuyến

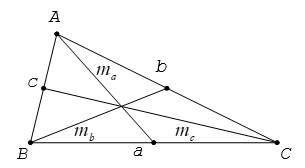
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.

Ta có

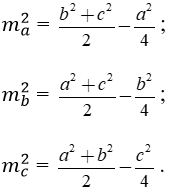
Xem thêm

Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức

Giải Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác

Câu 10:

12/07/2024

Tính giá trị biểu thức P = cos30⁰.cos60⁰ – sin30⁰.sin60⁰

A. $\sqrt{3}$

B. 2

C. 1

D. 0

Xem đáp án

Chọn D.

Vì 30⁰ và 60⁰ là hai góc phụ nhau nên

Do đó: P = cos30⁰.cos60⁰- sin30⁰.sin60⁰= cos30⁰.cos60⁰- cos30⁰.cos60⁰= 0.

Câu 11:

23/07/2024

Tính giá trị biểu thức P = sin30⁰.cos60⁰ + cos30⁰.sin60⁰

A. 1

B. 0

C. 2

D. $\sqrt{3}$

Xem đáp án

Chọn A.

Vì 30⁰ và 60⁰ là hai góc phụ nhau nên

Suy ra: P = sin30⁰.cos60⁰+ cos30⁰.sin60⁰= cos60⁰.cos60⁰+ sin60⁰.cos60⁰= 1.

Câu 12:

23/07/2024

Cho tam giác ABC vuông tại A có AC = 12; M là trung điểm AC. Tính $\vec{B M} . \vec{C A}$

A. 12

B. -36

C. 36

D. -72

Xem đáp án

Chọn D.

Ta có: AM = 6; (2 vecto ngược hướng).

(do AB và CA vuông góc với nhau).

Câu 13:

19/07/2024

Cho tứ giác lồi ABCD có AD = 6cm. Đặt $\vec{v} = \vec{A B} - \vec{D C} - \vec{C B}$ . Tính $\vec{v} . \vec{A D}$

A. 18

B. 32

C. 36

D. 40

Xem đáp án

Chọn C.

Ta có :

suy ra

Câu 14:

23/07/2024

Cho tam giác ABC có cạnh BC = 6cm và đường cao AH; H ở trên cạnh BC sao cho BH = 2HC. Tính $\vec{A B} . \vec{B C}$

A. -24

B. 24

C. 16

D. -12

Xem đáp án

Chọn A.

Ta có BH = 2HC nên BH = 4

Câu 15:

14/07/2024

Cho tam giác ABC có A(1; 2); B(-1; 1) và C(5; -1).Tính cosA.

Xem đáp án

Chọn B.

Ta có suy ra

Câu 16:

12/07/2024

Cho tam giác đều ABC cạnh a, với các đường cao AH và BK vẽ HI vuông góc với AC. Câu nào sau đây đúng?

A.

B.

C.

D. Cả ba câu trên.

Xem đáp án

Chọn D.

Phương án A: nên

nên đẳng thức ở phương án A là đúng.

Phương án B: nên

nên đẳng thức ở phương án B là đúng.

Phương án C:

Do đó: nên phương án C là đúng.

Câu 17:

14/07/2024

Cho tam giác đều ABC cạnh a; với các đường cao AH; BK vẽ HI ⊥ AC. Câu nào sau đây đúng?

A.

B .

C.

D.

Xem đáp án

Chọn C.

Phương án A: do

nên loại A

Phương án B: do = CB. CK.cos0⁰

= a²/2 nên loại B và D

Phương án C: do

Chọn C.

Câu 18:

19/07/2024

Cho 2 vectơ $\vec{a}; \vec{b}$ có $|\vec{a}| = 4; |\vec{b}| = 5; (\vec{a}; \vec{b}) = 120^{o}$ . Tính $|\vec{a} + \vec{b}|$

C. 21

D. 61

Xem đáp án

Chọn B.

Ta có: $|\vec{a} + \vec{b}| = \sqrt{{(\vec{a} + \vec{b})}^{2}} = \sqrt{{\vec{a}}^{2} + 2 \vec{a} \vec{b} + {\vec{b}}^{2}} = \sqrt{{|\vec{a}|}^{2} + 2 \vec{a} \vec{b} + {|\vec{b}|}^{2}} = \sqrt{4^{2} + 2.4.5 . (- 0, 5) + 5^{2}} = \sqrt{61}$

Câu 19:

27/11/2024

Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.

Tính giá trị của biểu thức $\vec{G A} . \vec{G B} + \vec{G B} . \vec{G C} + \vec{G C} . \vec{G A}$

A. -3a²

B. -2a²

C. -4 a²/3

D. 2a²

Xem đáp án

Đáp án đúng: C.

*Lời giải

Vì nên

Gọi M, N, P lần lượt là trung điểm của BC, CA, AB

Tam giác ABM đều nên

Theo định lý Pitago ta có:

Suy ra

*Phương pháp giải

- Sử dụng quy tắc trọng tâm trong tam giác

- Sử dụng tính chất về tam giác đều: GA = 2/3 AM

- Tương tự tìm ra GB, GC. sau đó thay vào biểu thức của trọng tâm để tính ra giá trị

*Lý thuyết về tích vô hướng và có hướng của 2 vectơ:

Tích vô hướng của hai vectơ

Trong không gian Oxyz, tích vô hướng của hai vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ được xác định bởi công thức:

$\vec{a} . \vec{b} = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$

Ứng dụng của tích vô hướng

+ Cho vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ , khi đó độ dài của vectơ $\vec{a}$ được tính theo công thức:

$|\vec{a}| = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{2}^{2}}$

+ Cho hai điểm $A (x_{A}; y_{A}; z_{A})$ và $B (x_{B}; y_{B}; z_{B})$ . Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ $\vec{A B}$ . Do đó ta có

+ Cho vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Khi đó góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ được tính theo công thức:

$\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}}{\sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2} + b_{3}^{2}}}$ (với $\vec{a}, \vec{b} \neq \vec{0}$ )

+ Hai vectơ vuông góc: Cho vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Khi đó: $\vec{a} . \vec{b} = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$

$\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} = 0$

Tích có hướng của hai vectơ

Trong không gian Oxyz cho hai vectơ $\vec{a} = (a_{1}; a_{2}; a_{3})$ , $\vec{b} = (b_{1}; b_{2}; b_{3})$ . Tích có hướng của hai vectơ $\vec{a}$ và $\vec{b},$ kí hiệu là $[\vec{a}, \vec{b}]$ , được xác định bởi

$[\vec{a}, \vec{b}] = (|\begin{matrix} a_{2} & a_{3} \\ b_{2} & b_{3} \end{matrix}|; |\begin{matrix} a_{3} & a_{1} \\ b_{3} & b_{1} \end{matrix}|; |\begin{matrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{matrix}|) = (a_{2} b_{3} - a_{3} b_{2}; a_{3} b_{1} - a_{1} b_{3}; a_{1} b_{2} - a_{2} b_{1})$

Tính chất của tích có hướng:

$\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} = 0$

Xem thêm các bài viết liên quan hay, chi tiết:

Tích vô hướng của hai vectơ và cách giải bài tập

Bài toán về tích vô hướng và tích có hướng của hai vectơ

80 câu trắc nghiệm Vectơ cơ bản

Câu 20:

12/07/2024

Cho hai điểm A( -3;2) : B(4;3). Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M

A. M(7; 0)

B. M(5; 0)

C. M(3; 0)

D. tất cả sai

Xem đáp án

Chọn C.

Gọi M(x; 0) với x > 0.

Khi đó

Để tam giác MAB vuông tai M khi và chỉ khi

$\Leftrightarrow (x - 3) (x + 2) = 0 \Leftrightarrow [\begin{matrix} x - 3 = 0 \\ x + 2 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 3 (T M) \\ x = - 2 (l o ạ i) \end{matrix}$