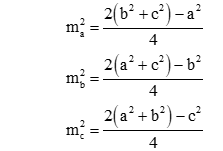Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án
Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án
-
459 lượt thi
-
55 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho tam giác ABC có AB = 4, AC = 6, Độ dài cạnh BC là:
 Xem đáp án
Xem đáp án
Áp dụng định lí cô sin trong tam giác ta có:
.
Chọn B.
Câu 2:
12/07/2024Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Giá trị cos A bằng
 Xem đáp án
Xem đáp án
Áp dụng hệ quả của định lí cô sin trong tam giác ta có:
.
Chọn A.
Câu 3:
18/07/2024Cho tam giác ABC có a = 3, b = 5, c = 6. Giá trị của bằng
 Xem đáp án
Xem đáp án
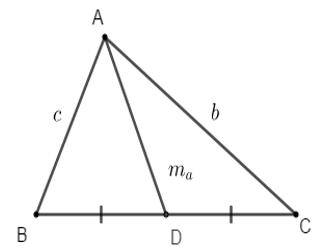
Áp dụng công thức độ dài đường trung tuyến ta có:
.
Chọn B.
Câu 4:
19/07/2024Cho tam giác ABC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Sử dụng công thức trung tuyến, ta có:
Chọn D
Câu 5:
15/07/2024Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
 Xem đáp án
Xem đáp án
Áp dụng định lí sin trong tam giác ta có. Suy ra:
.
Chọn A.
Câu 6:
15/07/2024Cho tam giác ABC có AB = 10, AC = 12, .Diện tích của tam giác ABC là:
 Xem đáp án
Xem đáp án
.
Chọn B.
Câu 7:
28/11/2024Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp của tam giác ABC bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải
Ta có:
⇒ ∆ABC vuông tại A.
Diện tích tam giác ABC là:
.
Nửa chu vi của tam giác là .
Bán kính đường tròn nội tiếp của tam giác ABC là:
. Chọn D.
*Phương pháp giải:
Sử dụng diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b và AB = c, r là bán kính đường tròn nội tiếp tam giác ABC, 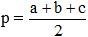
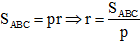
*Lý thuyết:
- Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.
2. Định lí
- Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
- Trong tam giác đều, tâm của đường tròn ngoại tiếp trùng với tâm của đường tròn nội tiếp và được gọi là tâm của đa giác đều.
3. Mở rộng
- Bán kính đường tròn ngoại tiếp đa giác là khoảng cách từ tâm đến đỉnh.
- Bán kính đường tròn nội tiếp đa giác là khoảng cách từ tâm O đến một cạnh.
Cho n-giác đều cạnh a. Khi đó:
- Chu vi của đa giác: 2p = na (p là nửa chu vi).
- Mỗi góc ở đỉnh của đa giác có số đo bằng .
- Mỗi góc ở tâm của đa giác có số đo bằng .
- Bán kính đường tròn ngoại tiếp:
- Bán kính đường tròn nội tiếp:
- Liên hệ giữa bán kính đường tròn ngoại tiếp và nội tiếp: .
- Diện tích đa giác đều: .
Xem thêm
Chuyên đề Đường tròn ngoại tiếp. Đường tròn nội tiếp () - Toán 9
Câu 8:
15/07/2024Cho tam giác ABC có AC = 6, BC = 8. lần lượt là độ dài các đường cao đi qua các đỉnh A, B. Tỉ số bằng
 Xem đáp án
Xem đáp án
Ta có:
.
Chọn A.
Câu 9:
22/07/2024Cho tam giác ABC có a = 5, b = 6, c = 7. Diện tích của tam giác ABC bằng
 Xem đáp án
Xem đáp án
Nửa chu vi của tam giác ABC là:
Áp dụng công thức Hê- rông, diện tích tam giác ABC là:
.
Chọn C.
Câu 10:
12/07/2024Cho tam giác ABC có a = 3, b = 5, c = 6. Bán kính đường trong nội tiếp của tam giác bằng
 Xem đáp án
Xem đáp án
Nửa chu vi của tam giác ABC là:
Áp dụng công thức Hê- rông, diện tích tam giác ABC là:
Bán kính đường trong nội tiếp của tam giác là:
. Chọn A.
Câu 11:
21/07/2024Cho tam giác ABC có a = 5, b = 12, c = 13. Bán kính đường tròn ngoại tiếp R của tam giác bằng
 Xem đáp án
Xem đáp án
⇒ ∆ABC vuông tại C
Bán kính đường tròn ngoại tiếp tam giác ABC là .
Chọn C.
Câu 12:
12/07/2024Cho tam giác ABC có a = 2, , . Độ dài cạnh c là
 Xem đáp án
Xem đáp án
Áp dụng định lí cosin trong tam giác ta có:
Chọn D
Câu 13:
12/07/2024Cho tam giác ABC có . Giá trị của cos B là:
 Xem đáp án
Xem đáp án
Áp dụng hệ quả định lí cosin trong tam giác ta có:
Chọn B
Câu 14:
12/07/2024Cho tam giác ABC có a = 2, b = 3, . Số đo của góc C là
 Xem đáp án
Xem đáp án
Áp dụng hệ quả định lí cosin trong tam giác ta có:
Chọn D
Câu 15:
22/07/2024Cho tam giác ABC có . Số đo của góc A là
 Xem đáp án
Xem đáp án
Ta có: a2 = b2 +c2 – bc nên b2 + c2 – a2 = bc
Áp dụng hệ quả định lí cosin trong tam giác ta có:
Chọn C
Câu 16:
12/07/2024Cho tam giác ABC có . Số đo của góc A là
 Xem đáp án
Xem đáp án
Ta có:
Áp dụng hệ quả định lí cosin trong tam giác ta có:
Chọn A
Câu 18:
12/07/2024Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là
 Xem đáp án
Xem đáp án
Ta có: a2 + b2 = c2 nên tam giác ABC là tam giác vuông.
Chọn C
Câu 19:
21/07/2024Cho tam giác ABC có a = 8 cm, b = 9 cm, c = 10 cm. Tam giác ABC là
 Xem đáp án
Xem đáp án
Ta có:
Tam giác ABC có AB = c là cạnh lớn nhất. Do đó, góc C là góc lớn nhất.
Lại có: nên tam giác ABC là tam giác nhọn.
Chọn A
Câu 20:
12/07/2024Cho tam giác ABC có a = 6 cm, b = 7 cm, c = 10 cm. Tam giác ABC là
 Xem đáp án
Xem đáp án
Ta có:
Suy ra, tam giác ABC là tam giác tù.
Chọn B
Câu 21:
23/07/2024Cho tam giác ABC. Biểu thức P = ab.cos C + bc.cos A +ca. cosB bằng
 Xem đáp án
Xem đáp án
ĐÁP ÁN C
Ta có:
Suy ra:
Tương tự,
Do đó,
Câu 22:
22/07/2024Cho tam giác ABC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Áp dụng hệ quả định lí cô sin trong tam giác ta có:
Do đó,
ĐÁP ÁN B
Câu 23:
12/07/2024Cho tam giác ABC, có . Giá trị của là
 Xem đáp án
Xem đáp án
ĐÁP ÁN B
Áp dụng công thức đường trung tuyến trong tam giác ta có:
Câu 24:
12/07/2024Cho tam giác ABC có a = 4, b = 6, . Giá trị của c là
 Xem đáp án
Xem đáp án
Áp dụng công thức đường trung tuyến trong tam giác ta có:
ĐÁP ÁN A
Câu 25:
28/11/2024Cho tam giác ABC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
*Lời giải:
Ta có:
*Phương pháp giải
Sử dụng công thức tính độ dài đường trung tuyến trong tam giác:
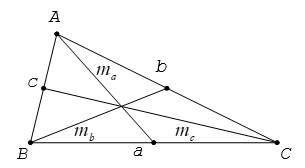
Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi ma; mb; mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và C của tam giác. Khi đó
*Lý thuyết:
Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.
- Các đường trung tuyến của tam giác giao nhau tại trọng tâm của tam giác.
- Trong tam giác ABC cân tại A và M là trung điểm của BC thì đường trung tuyến AM cũng là đường cao, đường phân giác và đường trung trực.
- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Độ dài đường trung tuyến: Gọi là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:
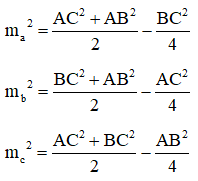
II. Các công thức.
Cho tam giác ABC vuông tại A, M là trung điểm của BC ta có: .
Gọi là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:
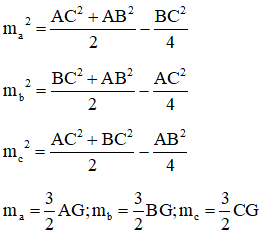
(với G là trọng tâm của tam giác ABC).
Xem thêm một số bài viết liên quan hay, chi tiết:
Công thức tính độ dài đường trung tuyến chi tiết nhất
Giải bài tập Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến
Câu 26:
11/07/2024Cho tam giác ABC trọng tâm G. Bình phương độ dài đoạn thẳng GA bằng
 Xem đáp án
Xem đáp án
Theo tính chất trọng tâm tam giác ta có: . Suy ra:
ĐÁP ÁN D
Câu 27:
23/07/2024tam giác ABC thỏa mãn c = a.cos B. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Theo hệ quả định lí cô sin trong tam giác ta có:
Từ giả thiết: c = a. cosB nên:
Do đó, tam giác ABC vuông tại A.
ĐÁP ÁN C
Câu 28:
23/07/2024Cho tam giác ABC có a = 30, . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Áp dụng định lí sin trong tam giác:
Suy ra:
ĐÁP ÁN A
Câu 29:
14/07/2024Cho tam giác ABC có a = 10 cm, . Diện tích của tam giác ABC là
 Xem đáp án
Xem đáp án
Diện tích tam giác ABC là:
ĐÁP ÁN B
Câu 30:
11/07/2024Cho tam giác ABC có AB = 4, AC =6, BC = 8. Diện tích của tam giác ABC là
 Xem đáp án
Xem đáp án
Nửa chu vi tam giác ABC là:
Áp dụng công thức Hê- rông, diện tích tam giác ABC:
ĐÁP ÁN A
Câu 31:
11/07/2024Cho tam giác ABC có AB = 4, AC = 6, A =30°. Diện tích của tam giác ABC là
 Xem đáp án
Xem đáp án
Diện tích tam giác ABC là:
ĐÁP ÁN B
Câu 32:
11/07/2024Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Bán kính đường tròn nội tiếp của tam giác bằng
 Xem đáp án
Xem đáp án
Ta có:
Suy ra, tam giác vuông tại A.
Diện tích tam giác ABC là:
Nửa chu vi tam giác:
Bán kính đường tròn nội tiếp của tam giác là:
ĐÁP ÁN A
Câu 33:
12/07/2024Cho tam giác ABC có a = 7, b = 8, c = 9. Bán kính đường tròn nội tiếp tam giác bằng
 Xem đáp án
Xem đáp án
Nửa chu vi tam giác:
Áp dụng công thức Hê- rông, diện tích tam giác ABC
Bán kính đường tròn nội tiếp của tam giác là
ĐÁP ÁN C
Câu 34:
18/07/2024Cho tam giác ABC có a = 5, b = 7, c = 8. Bán kính đường tròn ngoại tiếp tam giác bằng
 Xem đáp án
Xem đáp án
Nửa chu vi tam giác
Áp dụng công thức Hê- rông, diện tích tam giác ABC
Bán kính đường tròn ngoại tiếp tam giác:
ĐÁP ÁN B.
Câu 35:
17/07/2024Đáp án nào sau đây phù hợp với diện tích của hình lục giác ở hình bên?
 Xem đáp án
Xem đáp án
Hình lục giác đã cho là hợp của 2 tam giác đều có độ dài cạnh là 4 và 1 hình chữ nhật với độ dài 2 cạnh là 4 và 6.
Diện tích mỗi tam giác đều là .
Diện tích hình chữ nhật là 24.
Diện tích của hình lục giác là:
ĐÁP ÁN D
Câu 36:
17/07/2024Bề mặt viên gạch hình lục lăng có dạng hình lục giác đều cạnh 8 cm. Diện tích bề mặt của viên gạch là
 Xem đáp án
Xem đáp án
Gọi O là tâm của hình lục giác đều – O là giao điểm các đường chéo.
Hình lục giác đều cạnh 8 cm được chia thành sáu tam giác đều cạnh 8 cm.
Diện tích mỗi tam giác đều là .
Diện tích lục giác là .
ĐÁP ÁN C
Câu 37:
12/07/2024Tam giác cân cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là
 Xem đáp án
Xem đáp án
Giả sử tam giác ABC cân tại C, AC = BC = a, C = α
Diện tích tam giác là:
ĐÁP ÁN B
Câu 38:
19/07/2024Đa giác đều n đỉnh và nội tiếp đường tròn bán kính R có diện tích là
 Xem đáp án
Xem đáp án
Gọi O là tâm đa giác, giả sử A, B là hai đỉnh kề nhau của đa giác
Ta có . Diện tích đa giác đều bằng.
ĐÁP ÁN A
Câu 39:
13/07/2024Đáp án nào sau đây phù hợp với diện tích của phần được tô ở hình bên?
 Xem đáp án
Xem đáp án
Diện tích phần được tô màu bằng hiệu diện tích của hình vuông cạnh 8cm và 4 tam giác bằng nhau có 1 cạnh bằng 8 và đường cao ứng với cạnh đó bằng 2 cm.
Diện tích của 1 tam giác là:
Diện tích hình vuông là:
Diện tích phần tô đậm là: 64 – 4.8 = 32.
ĐÁP ÁN B
Câu 40:
12/07/2024Đáp án nào sau đây phù hợp với diện tích của tam giác ABC trong hình bên?
 Xem đáp án
Xem đáp án
ĐÁP ÁN B
Câu 41:
11/07/2024Cho tam giác ABC có bc = 4S. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
ĐÁP ÁN D
Ta có: (1)
Theo giả thiết ta có: bc = 4S (2)
Từ (1) (2) suy ra:
Câu 42:
20/07/2024Cho tam giác ABC có a = BC, b = CA, c = AB. Biểu thức cot A bằng
 Xem đáp án
Xem đáp án
Theo định lí sin trong tam giác ta có:
ĐÁP ÁN C
Câu 43:
19/07/2024Cho tam giác ABC. Biểu thức cot A bằng
 Xem đáp án
Xem đáp án
Theo định lí sin trong tam giác ta có:
ĐÁP ÁN A
Câu 44:
12/07/2024Cho tam giác ABC có a = BC, b = CA, c = AB. Biểu thức cot A bằng
 Xem đáp án
Xem đáp án
Diện tích tam giác ABC là:
ĐÁP ÁN D
Câu 45:
20/07/2024Cho tam giác ABC có a = BC, b = CA, c = AB. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
* Diện tích tam giác ABC là:
* Tương tự, ta có:
* Do đó,
ĐÁP ÁN B
Câu 46:
22/07/2024Cho tam giác ABC. Nếu a = 2b thì
 Xem đáp án
Xem đáp án
Ta có:
Tương tự,
Theo giả thiết a= 2b nên
ĐÁP ÁN A
Câu 47:
22/07/2024Cho tam giác ABC có a = BC, b = CA, c = AB, a + b = 2c. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Theo định lí sin trong tam giác ta có:
Tương tự, b = 2RsinB; c= 2R.sin C
Theo đầu bài:
a + b =2c ⇒ 2Rsin A + 2Rsin B = 4Rsin C ⇒ sin A + sin B = 2sin C.
ĐÁP ÁN C
Câu 48:
22/07/2024Cho tam giác ABC có a = BC, b = CA, c = AB, . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Theo định lí sin trong tam giác ta có:
Tương tự,
Ta có:
Hay
ĐÁP ÁN A
Câu 49:
15/07/2024Cho tam giác ABC có a = BC, b = CA, c = AB. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Theo định lí sin trong tam giác ta có:
Tương tự,
Theo bất đẳng thức tam giác ta có: a + b > c
Do đó, 2Rsin A + 2Rsin B > 2Rsin C ⇒ sin A + sin B > sin C
Tương tự, sin A + sin C > sin B và sin B + sin C > sin A
Vậy D sai.
ĐÁP ÁN D
Câu 50:
15/07/2024Một đa giác đều có góc ở mỗi đỉnh bằng α và nội tiếp đường tròn bán kính R thì có độ dài mỗi cạnh là:
 Xem đáp án
Xem đáp án
ĐÁP ÁN B
Giả sử A, B, C là ba đỉnh liên tiếp của đa giác đều.
Tam giác ABC cân tại B có góc ở đỉnh là α, góc ở đáy là .
Tam giác ABC nội tiếp đường tròn bán kính R nên
Câu 51:
14/11/2024Cho tam giác ABC. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Ta có:
Suy ra:
*Phương pháp giải
- Căn cứ vào đáp án, ta sẽ áp dụng công thức tính diện tích dùng hệ thức lượng và diện tích tam giác vuông
+) S = pr =
*Lý thuyến cần nắm và dạng toán về hệ thức lượng trong tam giác:
Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
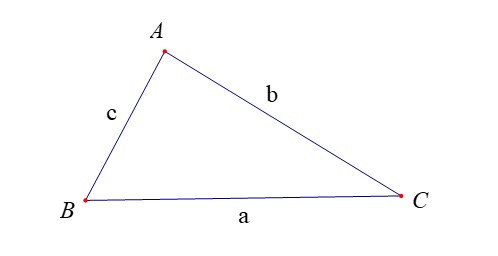
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Định lí sin
Trong tam giác ABC: .
Độ dài đường trung tuyến
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.
Ta có
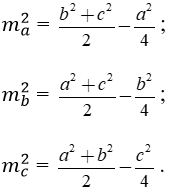
Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Công thức tính diện tích tam giác
Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Ta có các công thức tính diện tích tam giác ABC sau:
+) S = pr =
+) S = bc sin A = ca sin B =ab sin C.
+) S =
+) Công thức Heron: S = .
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức
Giải Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác
Chuyên đề Hệ thức lượng trong tam giác lớp 10 (Kết nối tri thức) | Chuyên đề dạy thêm Toán 10
Câu 52:
15/07/2024Cho tam giác ABC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Áp dụng định lí sin trong tam giác:
Suy ra: b = 2R sin B; c = 2R . sin C
Ta có, nên :
ĐÁP ÁN C
Câu 53:
12/07/2024Cho tam giác nhọn ABC nội tiếp (O; R). Diện tích của tam giác ABC bằng
 Xem đáp án
Xem đáp án
Ta có:
( góc ở tâm gấp 2 lần số đo góc nội tiếp cùng chắn 1 cung )
=
.
ĐÁP ÁN A
Có thể bạn quan tâm
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án) (2924 lượt thi)
- Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án (458 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết) (416 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Thông hiểu) (315 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Vận dụng) (400 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ (có đáp án) (2544 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (1192 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (1145 lượt thi)
- Trắc nghiệm Hình học Ôn tập chương 2 (có đáp án) (834 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Nhận biết) (534 lượt thi)
- Trắc nghiệm: Giá trị lượng giác của một góc bất kì 0° đến 180° (534 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Vận dụng) (506 lượt thi)
- Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án (478 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu) (379 lượt thi)
- Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Nhận biết) (365 lượt thi)