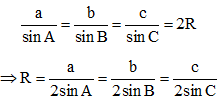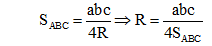Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)
Trắc nghiệm Toán 10 Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
-
3065 lượt thi
-
27 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
07/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
* Phương pháp giải:
- Sử dụng công thức Hê-rông để tính diện tích tam giác do đã biết độ dài 3 cạnh của tam giác.
- Công thức Hê-rông: S=√p(p-a)(p-b)(p-c)
* Lời giải:
Ta có: Nửa chu vi ΔABC:p=a+b+c2
Áp dụng công thức Hê-rông:
S=√p(p−a)(p−b)(p−c)=√12(12−6)(12−8)(12−10)=24
* Mở rộng: "Các công thức tính diện tích tam giác"
Cho tam giác có BC = a, AC = b, AB = c với:
• ha, hb, hc là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• p=a+b+c2 là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
S=12aha=12bhb=12chcS=12bcsinA=12casinB=12absinCS=abc4RS=prS=√p(p-a)(p-b)(p-c)
(Công thức Hê-rông)
→Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 2:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
Câu 3:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
Câu 4:
12/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
*Phương pháp giải
Tính quãng đường của hai tàu di chuyển được sau 2 tiếng. Giả sử hướng đi của tàu thứ nhất là AB, hướng đi của tàu thứ hai là AC, hai hướng tạo với nhau góc , sử dụng định lí cosin để tính được khoảng cách giữa hai tàu (cạnh AC).
- Định lí Côsin:
Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.
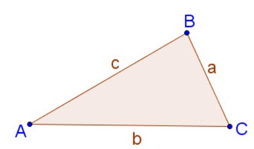
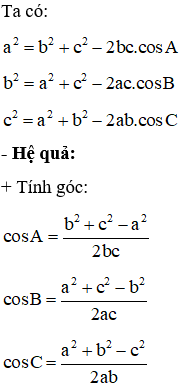
*Lời giải
Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là:
Sau 2h quãng đường tàu thứ hai chạy được là:
Vậy sau 2h hai tàu cách nhau là:
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Định lí côsin và định lí sin
Giải bài tập Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế
Câu 5:
05/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : B
- Khoảng cách AB là 91m.
Giải thích:
Lời giải
Ta có: Trong tam giác vuông CDA:
Trong tam giác vuông CDB:
Suy ra: khoảng cách
* Mở rộng:
Giải tam giác
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
– Biết độ dài ba cạnh;
– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
Ví dụ: Cho tam giác ABC có AB = 4, BC = 6, AC = . Điểm M thuộc đoạn BC sao cho MC = 2MB.
a) Tính cos các góc của tam giác ABC.
b) Tính độ dài cạnh AM.
Hướng dẫn giải:
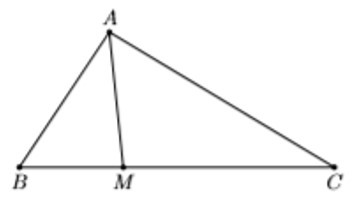
a) Theo định lí cosin trong tam giác ABC ta có:
cosB = = =
⇒ = 60°.
cosC = = =
cosA = = =
b) Ta có:
MC = 2MB ⇒ = ⇒ =
⇒ MB = BC = .6 = 2
Áp dụng định lí côsin trong tam giác AMB ta có:
AM2 = AB2 + BM2 – 2AB.BM.cosB = 42 + 22 – 2.4.2. = 12
⇒ AM = =
Ví dụ: Cho tam giác ABC có ; và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).
Hướng dẫn giải:
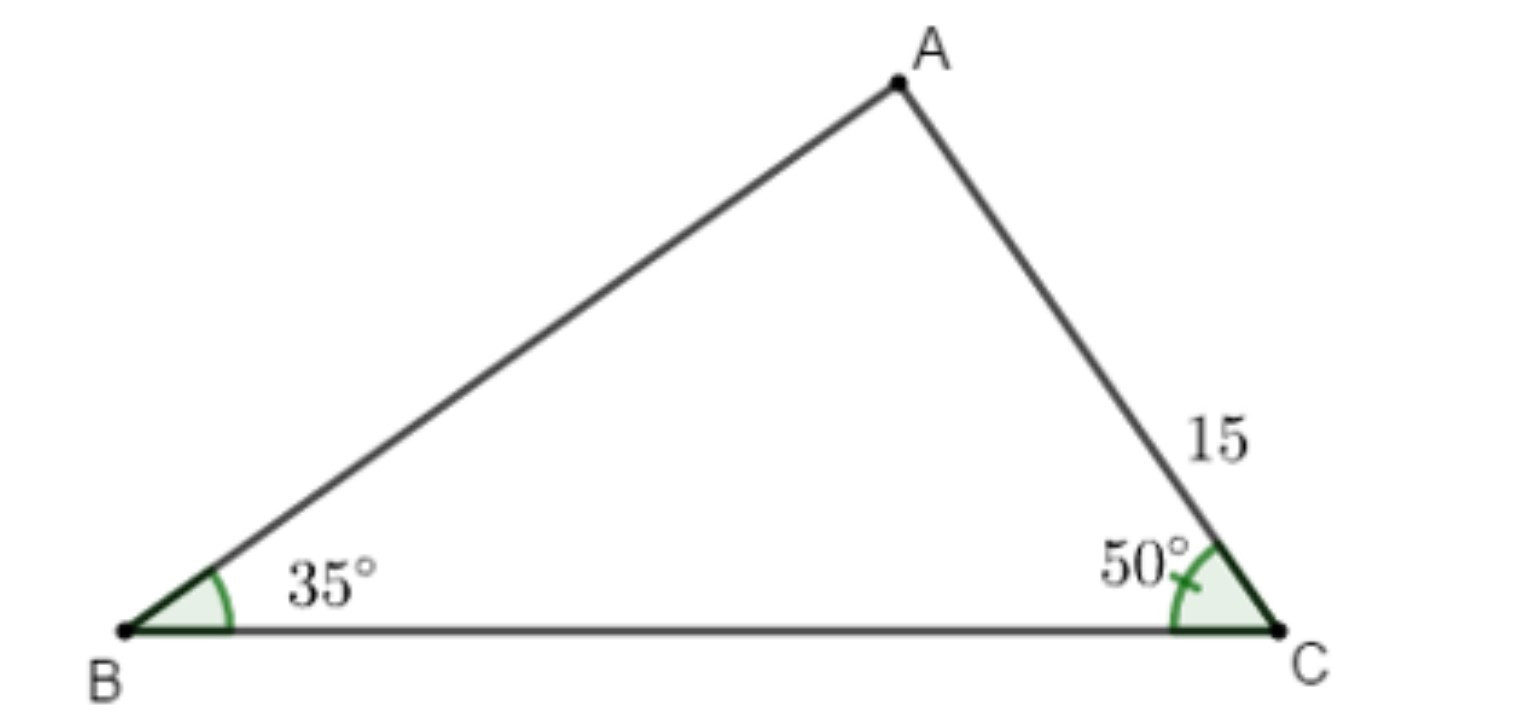
Ta có:
+ + = 180° (tổng ba góc trong tam giác)
Suy ra:
= 180° – – = 180° – 35° – 50° = 95°
Áp dụng định lí sin trong tam giác ABC ta có:
= =
Suy ra:
BC = = ≈ 26,05cm
AB = = ≈ 20,03cm
Vậy BC = 26,05cm và AB ≈ 20,03 cm.
Xem thêm các bài viết liên quan,chi tiết khác:
Lý thuyết Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác – Cánh diều
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Chọn
Không có đáp án
Ta có:
Câu 7:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có: Trong
Câu 10:
07/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
*Phương pháp giải:
Tính được giá trị lượng giác của các góc trong tam giác khi biết được số đo của ba cạnh trong tam giác. Từ đó tính ra được số đo của góc cần tìm.
*Lời giải
Ta có:
Xem thêm một số bài viết liên quan hay, chi tiết:
Câu 11:
06/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Lời giải
Ta có: Trong tam giác ABC:
Mặt khác
*Phương pháp giải:
Tính góc C lấy 180 trừ 2 góc A và B
Sử dụng định lí sin
*Lý thuyết;
Định lí sin trong tam giác
Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
Trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
Xem thêm
Lý thuyết Định lí côsin và định lí sin – Toán 10 Chân trời sáng tạoCâu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
Câu 15:
12/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng : B
*Phương pháp giải:
áp dụng công thức tính S tam giác bằng hệ thức lượng: =bcsinA= casinB= absinC
*Lời giải
Ta có:
* Các công thức tính diện tích tam giác bằng hệ thức lượng:
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
(Công thức Hê-rông)
Xem thêm các bài viết liên quan hay, chi tiết:
Bài tập Hệ thức lượng trong tam giác có đáp án
Bài tập hệ thức lượng nâng cao(có đáp án)
Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)
Câu 16:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có:
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
Câu 19:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
Mà:
suy ra: .
Câu 20:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có: Một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2).
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có:
Suy ra:
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
Câu 23:
07/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
*Phương pháp giải:
- Sử dụng công thức Hê-rông để tính diện tích tam giác do đã biết độ dài 3 cạnh của tam giác.
- Công thức Hê-rông:
- Sử dụng công thức để tính được bán kính khi đã biết độ dài 3 cạnh và diện tích của tam giác.
*Lời giải
Ta có:
Suy ra:
Mà
* Mở rộng: "Một số phương pháp giải bài toán liên quan đến tính bán kính đường tròn ngoại tiếp"
Phương pháp 1: Sử dụng đinh lý sin trong tam giác
Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:
Phương pháp 2: Sử dụng diện tích tam giác
là nửa chu vi
(Công thức Hê-rông)
Phương pháp 3: Sử dụng trong hệ tọa độ
- Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC
- Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có)
- Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm
R = OA = OB = OC.
Phương pháp 4: Sử dụng trong tam giác vuông (kiến thức lớp 9)
Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền, do đó bán kính đường tròn ngoại tiếp tam giác vuông chính bằng nửa độ dài cạnh huyền.
Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 24:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
Câu 25:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có:
Mặt khác:
(Vì ).
Mà:
Câu 26:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có: cùng phương suy ra:
Câu 27:
09/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Phương pháp giải:
- Tìm các tọa độ vecto AB và AC dựa vào dữ kiện dề bài cho
- Tính góc BAC theo công thức định lý côsin trong tam giác
*Lời giải:
Ta có: , .
Suy ra:
* Các dạng bài tập và lý thuyết thêm
a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Định lí Côsin .
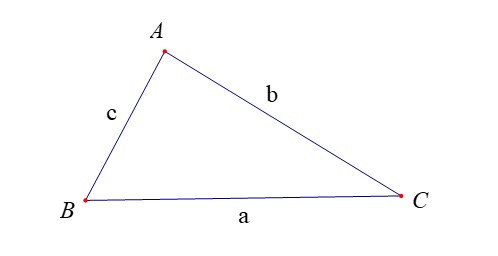
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
2. Định lí sin
Trong tam giác ABC: .
3. Công thức tính diện tích tam giác
Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Ta có các công thức tính diện tích tam giác ABC sau:
+) S = pr =
+) S = bc sin A = ca sin B =ab sin C.
+) S =
+) Công thức Heron: S = .
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án)
Có thể bạn quan tâm
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án) (3064 lượt thi)
- Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án (509 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết) (459 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Thông hiểu) (351 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Vận dụng) (435 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ (có đáp án) (2635 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (1340 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (1278 lượt thi)
- Trắc nghiệm Hình học Ôn tập chương 2 (có đáp án) (885 lượt thi)
- Trắc nghiệm: Giá trị lượng giác của một góc bất kì 0° đến 180° (578 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Nhận biết) (572 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Vận dụng) (540 lượt thi)
- Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án (535 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu) (411 lượt thi)
- Trắc nghiệm Tích vô hướng của hai vectơ (có đáp án) (397 lượt thi)