Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết)
Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết)
-
408 lượt thi
-
15 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 3:
22/07/2024Trong tam giác ABC có:
Xem đáp án
Đáp án A
Trong tam giác ABC, độ dài trung tuyến kẻ từ đỉnh A là
Câu 6:
23/07/2024Trong tam giác ABC, tìm hệ thức sai?
Xem đáp án
Đáp án C
+)
Suy ra . Suy ra mệnh đề đáp án A và B đúng
+) suy ra . Suy ra mệnh đề đáp án D đúng
Câu 8:
22/07/2024Cho tam giác ABC có AB = 4cm, BC = 7cm, CA = 9cm. Giá trị cosA là:
Xem đáp án
Đáp án A
Ta có:
Câu 9:
22/07/2024Cho tam giác ABC có và AB = 5. Kết quả nào trong các kết quả sau là độ dài của cạnh AC?
Xem đáp án
Đáp án B
Câu 10:
23/07/2024Cho tam giác ABC có và AC = 6. Kết quả nào trong các kết quả sau là độ dài cạnh BC?
Xem đáp án
Đáp án D
+ Có
+
Câu 11:
22/07/2024Cho tam giác ABC có b = 10, c = 16 và góc . Kết quả nào trong các kết quả sau là độ dài của cạnh BC?
Xem đáp án
Đáp án B
Suy ra
Câu 12:
22/07/2024Tam giác ABC có AB = 2, AC = 1 và . Tính độ dài cạnh BC?
Xem đáp án
Đáp án D
Theo định lí hàm cosin, ta có:
Câu 13:
23/07/2024Tam giác ABC có và . Tính độ dài cạnh BC
Xem đáp án
Đáp án B
Theo định lí hàm cosin, ta có:
Câu 14:
22/07/2024Cho tam giác ABC có a = 10, b = 6 và c = 8. Kết quả nào trong các kết quả sau là số đo độ dài của trung tuyến AM?
Xem đáp án
Đáp án B
Câu 15:
06/12/2024Tam giác ABC có AB = 9cm, AC = 12cm, và BC = 15cm. Tính độ dài đường trung tuyến AM của tam giác đã cho
Xem đáp án
Đáp án đúng là A
Lời giải
Áp dụng hệ thức đường trung tuyến: ta được:
*Phương pháp giải:
Áp dụng hệ thức tính độ dài đường trung tuyến
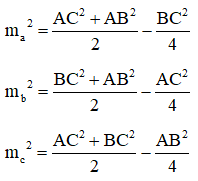
*Lý thuyết:
Đường trung tuyến của tam giác
– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).
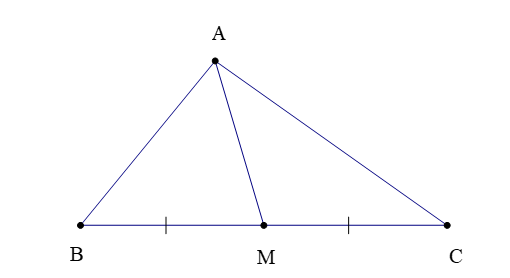
Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.
– Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.
Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.
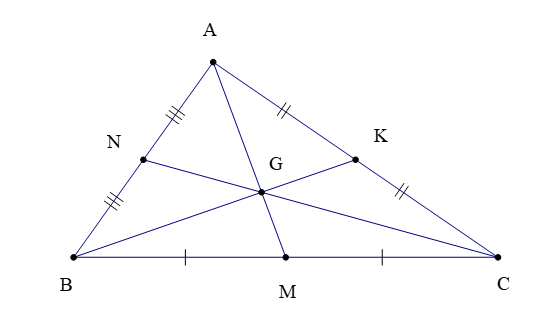
Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.
Nhận xét: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G là trọng tâm ta có:
- Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.
- Các đường trung tuyến của tam giác giao nhau tại trọng tâm của tam giác.
- Trong tam giác ABC cân tại A và M là trung điểm của BC thì đường trung tuyến AM cũng là đường cao, đường phân giác và đường trung trực.
- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Độ dài đường trung tuyến: Gọi là độ dài đường trung tuyến lần lượt vẽ từ đỉnh A, B, C của tam giác ABC, ta có:
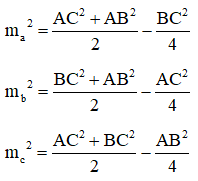
Xem thêm
Lý thuyết Tính chất ba đường trung tuyến của tam giác – Toán 7 Cánh diều