30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ

Câu 1:

23/07/2024

Rút gọn biểu thức sau $A = \frac{\cot^{2} x - \cos^{2} x}{\cot^{2} x} + \frac{\sin x . \cos x}{\cot x}$ .

A. A=1.

B. A=2.

C. A=3.

D. A=4

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$A = \frac{\cot^{2} x - \cos^{2} x}{\cot^{2} x} + \frac{\sin x . \cos x}{\cot x} = 1 - \frac{\cos^{2} x}{\cot^{2} x} + \frac{\sin x . \cos x}{\cot x} = 1 - \sin^{2} x + \sin^{2} x = 1$

Câu 2:

09/10/2024

Cho biết

\tan α = \frac{1}{2}

. Tính

\cot α

.

A. $\cot α = 2$ .

B. $\cot α = \sqrt{2}$ .

C. $\cot α = \frac{1}{4}$ .

D. $\cot α = \frac{1}{2}$ .

Xem đáp án

Đáp án đúng: A

*Phương pháp giải:

- Áp dụng tính chất của giá trị lượng giác đặc biệt, quy tắc nhân lượng giác, hằng đẳng thức để thực hiên phép tính

*Lời giải:

$\tan α . \cot α = 1 \Rightarrow \cot x = \frac{1}{\tan x} = 2$

*Các lý thuyết cần nằm về lượng giác

a. Công thức cộng:

$\sin (a + b) = \sin a . \cos b + \sin b . \cos a$

$\sin (a - b) = \sin a . \cos b - \sin b . \cos a$

$\cos (a + b) = \cos a . \cos b - \sin a . \sin b$

$\cos (a - b) = \cos a . \cos b + \sin a . \sin b$

$\tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a . \tan b}$

$\tan (a - b) = \frac{\tan a - \tan b}{1 + \tan a . \tan b}$

b. Công thức nhân đôi, hạ bậc:

* Công thức nhân đôi:

$\sin 2 α = 2 \sin α . \cos α$

$\cos 2 α = \cos^{2} α - \sin^{2} α = 2 \cos^{2} α - 1 = 1 - 2 \sin^{2} α$

$\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}$

* Công thức hạ bậc:

$\begin{matrix} \sin^{2} α = \frac{1 - \cos 2 α}{2} \\ \cos^{2} α = \frac{1 + \cos 2 α}{2} \\ \tan^{2} α = \frac{1 - \cos 2 α}{1 + \cos 2 α} \end{matrix}$

* Công thức nhân ba:

$\begin{array}{l} \sin 3 α = 3 \sin α - 4 \sin^{3} α \\ c o s 3 α = 4 c o s^{3} α - 3 c o s α \end{array}$

c. Công thức biến đổi tích thành tổng:

$\begin{array}{l} \cos a \cos b = \frac{1}{2} [\cos (a + b) + \cos (a - b)] \\ \sin a \sin b = - \frac{1}{2} [\cos (a + b) - \cos (a - b)] \\ \sin a \cos b = \frac{1}{2} [\sin (a + b) + \sin (a - b)] \end{array}$

d. Công thức biển đổi tổng thành tích:

$\cos a + \cos b = 2 \cos \frac{a + b}{2} . \cos \frac{a - b}{2}$

$\cos a - \cos b = - 2 \sin \frac{a + b}{2} . \sin \frac{a - b}{2}$

$\sin a + \sin b = 2 \sin \frac{a + b}{2} . \cos \frac{a - b}{2}$

$\sin a - \sin b = 2 \cos \frac{a + b}{2} . \sin \frac{a - b}{2}$

$\tan a + \tan b = \frac{\sin (a + b)}{\cos a . \cos b}$

$\tan a - \tan b = \frac{\sin (a - b)}{\cos a . \cos b}$

$\cot a + \cot b = \frac{\sin (a + b)}{\sin a . \sin b}$

$\cot a - \cot b = \frac{\sin (b - a)}{\sin a . \sin b}$

*Các dạng bài lượng giác của một góc bất kì từ 0-180

a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản

50 Bài tập Hàm số lượng giác mới nhất

Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án

Câu 3:

24/10/2024

Trong các mệnh đề sau, mệnh đề nào sai?

A. ${(\sin x \cos x)}^{2} = 12 \sin x \cos x$

B. $\sin^{4} x + \cos^{4} x = 12 \sin^{2} x \cos^{2} x$

C. ${(\sin x + \cos x)}^{2} = 1 + 2 \sin x \cos x$

D. $\sin^{6} x + \cos^{6} x = 1 \sin^{2} x \cos^{2} x$

Xem đáp án

Đáp án đúng: D

*Lời giải

$\sin^{6} x + \cos^{6} x = {(\sin^{2} x)}^{3} + {(\cos^{2} x)}^{3} = {(\sin^{2} x + \cos^{2} x)}^{3} - 3 (\sin^{2} x + \cos^{2} x) . \sin^{2} x . \cos^{2} x = 1 - 3 \sin^{2} x . \cos^{2} x$

*Phương pháp giải:

- sử dụng các công thức cơ bản về lượng giác để biến đổi xem coi ý nào đúng:

$\sin^{2} x + \cos^{2} x = 1$

- áp dụng thêm cả kiến thức về hằng đẳng thức để biến đổi

* Lý thuyết và các dạng bài về giá trị lượng giác của một cung:

Các công thức lượng giác cơ bản:

CÁC DẠNG BÀI:

Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

Phương pháp giải:

Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác

Phương pháp giải:

Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 3: Rút gọn biểu thức lượng giác

Phương pháp giải:

Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm các bài viết liên quan hay, chi tiết:

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10

Trắc nghiệm Cung và góc lượng giác có đáp án – Toán lớp 10

Câu 4:

23/07/2024

Khẳng định nào sau đây là sai?

A. $\sin^{2} α + \cos^{2} α = 1$

B. $1 + \cot^{2} α = \frac{1}{\sin^{2} α} (\sin α \neq 0)$

C. $\tan α . \cot α = - 1 (\sin α . \cos α \neq 0)$

D. $1 + \tan^{2} α = \frac{1}{\cos^{2} α} (\cos α \neq 0)$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\tan α . \cot α = \frac{\sin x}{\cos x} . \frac{\cos x}{\sin x} = 1$

Câu 5:

09/10/2024

Biểu thức

f (x) = 3 (\sin^{4} x + \cos^{4} x) - 2 (\sin^{6} x + \cos^{6} x)

có giá trị bằng:

A. 1.

B. 2.

C. -3.

D. 0.

Xem đáp án

Đáp án đúng: A

*Phương pháp giải:

- Áp dụng tính chất của giá trị lượng giác đặc biệt, quy tắc công, nhân lượng giác,... để thực hiên phép tính

*Lời giải:

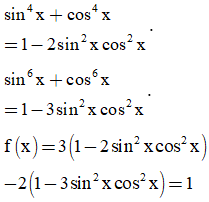
*Các lý thuyết cần nằm về lượng giác

a. Công thức cộng:

$\sin (a + b) = \sin a . \cos b + \sin b . \cos a$

$\sin (a - b) = \sin a . \cos b - \sin b . \cos a$

$\cos (a + b) = \cos a . \cos b - \sin a . \sin b$

$\cos (a - b) = \cos a . \cos b + \sin a . \sin b$

$\tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a . \tan b}$

$\tan (a - b) = \frac{\tan a - \tan b}{1 + \tan a . \tan b}$

b. Công thức nhân đôi, hạ bậc:

* Công thức nhân đôi:

$\sin 2 α = 2 \sin α . \cos α$

$\cos 2 α = \cos^{2} α - \sin^{2} α = 2 \cos^{2} α - 1 = 1 - 2 \sin^{2} α$

$\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}$

* Công thức hạ bậc:

$\begin{matrix} \sin^{2} α = \frac{1 - \cos 2 α}{2} \\ \cos^{2} α = \frac{1 + \cos 2 α}{2} \\ \tan^{2} α = \frac{1 - \cos 2 α}{1 + \cos 2 α} \end{matrix}$

* Công thức nhân ba:

$\begin{array}{l} \sin 3 α = 3 \sin α - 4 \sin^{3} α \\ c o s 3 α = 4 c o s^{3} α - 3 c o s α \end{array}$

c. Công thức biến đổi tích thành tổng:

$\begin{array}{l} \cos a \cos b = \frac{1}{2} [\cos (a + b) + \cos (a - b)] \\ \sin a \sin b = - \frac{1}{2} [\cos (a + b) - \cos (a - b)] \\ \sin a \cos b = \frac{1}{2} [\sin (a + b) + \sin (a - b)] \end{array}$

d. Công thức biển đổi tổng thành tích:

$\cos a + \cos b = 2 \cos \frac{a + b}{2} . \cos \frac{a - b}{2}$

$\cos a - \cos b = - 2 \sin \frac{a + b}{2} . \sin \frac{a - b}{2}$

$\sin a + \sin b = 2 \sin \frac{a + b}{2} . \cos \frac{a - b}{2}$

$\sin a - \sin b = 2 \cos \frac{a + b}{2} . \sin \frac{a - b}{2}$

$\tan a + \tan b = \frac{\sin (a + b)}{\cos a . \cos b}$

$\tan a - \tan b = \frac{\sin (a - b)}{\cos a . \cos b}$

$\cot a + \cot b = \frac{\sin (a + b)}{\sin a . \sin b}$

$\cot a - \cot b = \frac{\sin (b - a)}{\sin a . \sin b}$

*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:

TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản

Giải bài tập Toán 10 Bài tập cuối chương 3

50 Bài tập Hàm số lượng giác mới nhất

Câu 6:

23/07/2024

Biểu thức:

f (x) = \cos^{4} x + \cos^{2} x \sin^{2} x + \sin^{2} x

có giá trị bằng

A. 1.

B. 2.

C. -2.

D. -1.

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$f (x) = \cos^{2} x (\cos^{2} x + \sin^{2} x) + \sin^{2} x = \cos^{2} x + \sin^{2} x = 1$

Câu 7:

23/07/2024

Biểu thức

\tan^{2} x \sin^{2} x - \tan^{2} x + \sin^{2} x

có giá trị bằng

A. -1.

B. 0 .

C. 2.

D. 1.

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

$\tan^{2} x \sin^{2} x - \tan^{2} x + \sin^{2} x = \tan^{2} x (\sin^{2} x - 1) + \sin^{2} x = \frac{\sin^{2} x}{\cos^{2} x} (- \cos^{2} x) + \sin^{2} x = 0$

Câu 8:

06/10/2024

Giá trị của

A = \tan 5^{°} . \tan 10^{°} . \tan 15^{°} ... \tan 80^{°} . \tan 85^{°}

là

A. 2.

B. 1.

C. 0.

D. -1.

Xem đáp án

Đáp án đúng: B

*Phương pháp giải:

- Áp dụng tính chất của giá trị lượng giác đặc biệt, quy tắc nhân lượng giác để thực hiên phép tính

*Lời giải:

A = tan5°.tan10°.tan15°....tan80°.tan85°

= (tan5°.tan85°).(tan10°.tan80°)....(tan40°.tan50°).tan45°= (tan5°.cot5°).(tan10°.cot10°)...(tan40°.cot40°).1 = 1.1...1.1 =1

*Các dạng bài lượng giác của một góc bất kì từ 0-180 $°$ a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10

Câu 9:

23/07/2024

Chọn mệnh đề đúng?

A. $\sin^{4} x - \cos^{4} x = 1 - 2 \cos^{2} x$ .

B.

\sin^{4} x - \cos^{4} x = 1 - 2 \sin^{2} x \cos^{2} x

C. $\sin^{4} x - \cos^{4} x = 1 - 2 \sin^{2} x$

D.

\sin^{4} x - \cos^{4} x = 2 \cos^{2} x - 1

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\sin^{4} x - \cos^{4} x = (\sin^{2} x - \cos^{2} x) (\sin^{2} x + \cos^{2} x) = (1 - \cos^{2} x) - \cos^{2} x = 1 - 2 \cos^{2} x$

Câu 10:

16/10/2024

Rút gọn biểu thức

P = \frac{1 - s i n^{2} x}{2 \sin x . \cos x}

ta được

A. $P = \frac{1}{2} \tan x$ .

B. $P = \frac{1}{2} \cot x$ .

C. $P = 2 \cot x$ .

D. $P = 2 \tan x$ .

Xem đáp án

Đáp án đúng: B

*Phương pháp giải:

- Áp dụng công thức công thức cộng trong lượng giác để biến đổi thực hiện phép tính

*Lời giải:

$P = \frac{1 - s i n^{2} x}{2 \sin x . \cos x} = \frac{\cos^{2} x}{2 \sin x . \cos x} = \frac{\cos x}{2 \sin x} = \frac{1}{2} \cot x$

*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo

Giải Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10

Câu 11:

23/07/2024

Giá trị của $B = \cos^{2} 73^{°} + \cos^{2} 87^{°} + \cos^{2} 3^{°} + \cos^{2} 17^{°}$ là

A. $\sqrt{2}$ .

B. 2.

C. -2.

D. 1.

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

$B = (\cos^{2} 73^{°} + \cos^{2} 17^{°}) + (\cos^{2} 87^{°} + \cos^{2} 3^{°}) = (\cos^{2} 73^{°} + \sin^{2} 73^{°}) + (\cos^{2} 87^{°} + \sin^{2} 87^{°}) = 2$

Câu 12:

23/07/2024

Cho

c o t α = \frac{1}{3}

. Giá trị của biểu thức

A = \frac{3 \sin α + 4 \cos α}{2 \sin α - 5 \cos α}

là:

A. $- \frac{15}{13}$ .

B. $- 13$ .

C. $\frac{15}{13}$ .

D. $13$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

$A = \frac{3 \sin α + 4 \sin α . \cot α}{2 \sin α - 5 \sin α . \cot α} = \frac{3 + 4 \cot α}{2 - 5 \cot α} = 13$

Câu 13:

20/10/2024

Giá trị của $\tan 30^{°} + \cot 30^{°}$ bằng bao nhiêu?

A. $\frac{4}{\sqrt{3}}$

B.

\frac{1 + \sqrt{3}}{3}

C. $\frac{2}{\sqrt{3}}$

D. 2.

Xem đáp án

Đáp án đúng: A

* Phương pháp giải

- Sử dụng bảng giá trị lượng giác của các góc đặc biệt để tìm ra giá trị của tan30 và cot30 rồi cộng chúng lại với nhau

* Lời giải

$\tan 30^{°} + \cot 30^{°} = \frac{\sqrt{3}}{3} + \sqrt{3} = \frac{4 \sqrt{3}}{3}$

* Lý thuyết và các dạng bài về giá trị lượng giác của một góc bất kì 0 đến 180:

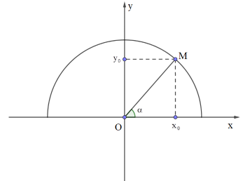
- Định nghĩa: Cho góc $α$ ( $0^{o} \leq α \leq 180^{o}$ ) bất kì, xác định một điểm $M (x_{0}; y_{0})$ trên nửa đường tròn đơn vị sao cho $\hat{x O M} = α$ . Khi đó ta có: $\sin α = y_{0}$ ; $\cos α = x_{0}$ ; $\tan α = \frac{y_{0}}{x_{0}} (x_{0} \neq 0)$ ; $\cot α = \frac{x_{0}}{y_{0}} (y_{0} \neq 0)$ . ( sin, cos, tan, cot là các giá trị lượng giác của góc $α$ )

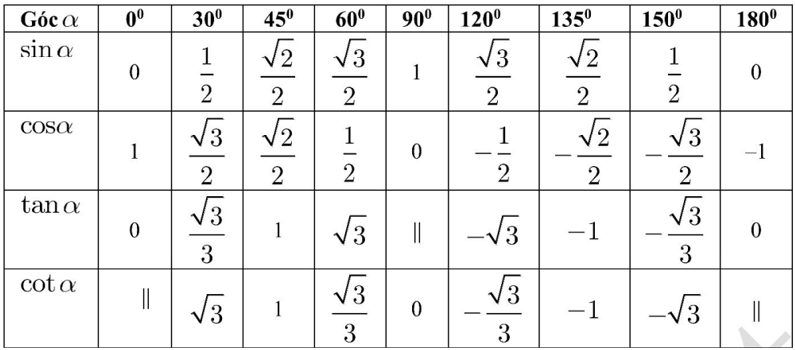
Bảng giá trị lượng giác của các góc đặc biệt:

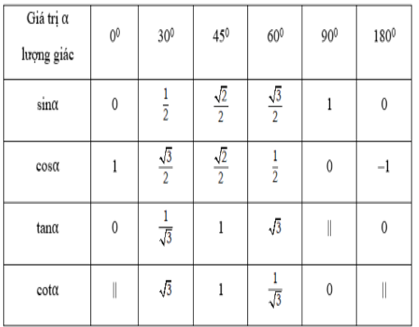
CẤC DẠNG BÀI:

Dạng 1: Góc và dấu của các giá trị lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.

Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.

Dạng 3: Chứng minh, rút gọn một biểu thức lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập (2024) chi tiết nhất

Giải Toán 10 Bài 1 (Cánh diều): Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án

Câu 14:

13/11/2024

Trong các đẳng thức sau đây, đẳng thức nào sai?

A. $\sin 0^{°} + \cos 0^{°} = 1$ .

B. $\sin 90^{°} + \cos 90^{°} = 1$ .

C. $\sin 180^{°} + \cos 180^{°} = - 1$ .

D. $\sin 60^{°} + \cos 60^{°} = 1$ .

Xem đáp án

Đáp án đúng là: D

Lời giải

Giá trị lượng giác của góc đặc biệt.

*Phương pháp giải:

Sử dụng bảng giá trị các góc đặc biệt

*Lý thuyết:

Xem thêm

Tổng hợp bảng giá trị lượng giác (2024) đầy đủ, chi tiết nhất

TOP 40 câu Trắc nghiệm Tỉ số lượng giác của góc nhọn và Bảng lượng giác (có đáp án 2024) - Toán 9

Câu 15:

23/07/2024

Trong các khẳng định sau, khẳng định nào sai?

A. $\cos 60^{°} = \sin 30^{°}$ .

B. $\cos 60^{°} = \sin 120^{°}$ .

C. $\cos 30^{°} = \sin 120^{°}$ .

D. $\sin 60^{°} = - \cos 120^{°}$ .

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Giá trị lượng giác của góc đặc biệt.

Câu 16:

23/07/2024

Giá trị của

\tan 45^{°} + \cot 135^{°}

bằng bao nhiêu?

A. 2.

B. 0.

C. $\sqrt{3}$ .

D. 1.

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

$\tan 45^{°} + \cot 135^{°} = 1 - 1 = 0$

Câu 17:

23/07/2024

Giá trị của

\cos 30^{°} + \sin 60^{°}

bằng bao nhiêu?

A. $\frac{\sqrt{3}}{3}$ .

B. $\frac{\sqrt{3}}{2}$

C. $\sqrt{3}$ .

D. 1.

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\cos 30^{°} + \sin 60^{°} = \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} = \sqrt{3}$

Câu 18:

17/10/2024

Giá trị của

E = \sin 36^{°} \cos 6^{°} \sin 126^{°} \cos 84^{°}

là

A. $\frac{1}{2}$ .

B. $\frac{\sqrt{3}}{2}$ .

C. 1.

D. -1.

Xem đáp án

Đáp án đúng: A

*Phương pháp giải:

- Áp dụng tính chất 2 góc phụ nhau biến đổi 2 góc 126 và 84 thành 2 góc nhỏ

*Lời giải:

$E = \sin 36^{°} \cos 6^{°} \sin (90^{°} + 36^{°}) \cos (90^{°} - 6^{°}) = \sin 36^{°} \cos 6^{°} - \cos 36^{°} \sin 6^{°} = \sin 30^{°} = \frac{1}{2}$

*Một số dạng bài thêm về giá trị lượng giác của một góc bất kì từ 0 đến 180:

Tính chất:

Hai góc bù nhau là hai góc có tổng bằng $180^{o}$ . Cho góc $α$ ta có:

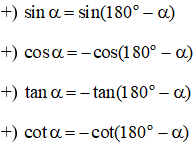
Hai góc phụ nhau là hai học có tổng bằng $90^{o}$ . Cho góc $α$ ta có:

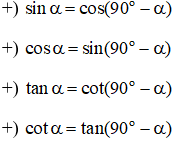
Các dạng bài.

Dạng 1: Góc và dấu của các giá trị lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.

Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập chi tiết nhất

Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10

Câu 19:

23/07/2024

Đẳng thức nào sau đây sai?

A. $\sin 45^{°} + \sin 45^{°} = \sqrt{2}$ .

B. $\sin 30^{°} + \cos 60^{°} = 1$ .

C. $\sin 60^{°} + \cos 150^{°} = 0$ .

D. $\sin 120^{°} + \cos 30^{°} = 0$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Giá trị lượng giác của góc đặc biệt.

Câu 20:

23/07/2024

Cho hai góc nhọn

α

và

β

(

α < β)

. Khẳng định nào sau đây là sai?

A. $\cos α < \cos β$ .

B. $\sin α < \sin β$ .

C. $\tan α + \tan β > 0$ .

D. $\cot α > \cot β$ .

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Biểu diễn lên đường tròn.

Câu 21:

23/07/2024

Cho

Δ A B C

vuông tại A, góc B bằng

30^{°}

. Khẳng định nào sau đây là sai?

A. $\cos B = \frac{1}{\sqrt{3}}$ .

B. $\sin C = \frac{\sqrt{3}}{2}$ .

C. $\cos C = \frac{1}{2}$ .

D. $\sin B = \frac{1}{2}$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\cos B = \cos 30^{°} = \frac{\sqrt{3}}{2}$

Câu 22:

23/07/2024

Tìm khẳng định sai trong các khẳng định sau:

A. $\cos 75^{°} > \cos 50^{°}$ .

B. $\sin 80^{°} > \sin 50^{°}$ .

C. $\tan 45^{°} < \tan 60^{°}$ .

D. $\cos 30^{°} = \sin 60^{°}$ .

Xem đáp án

Đáp án: A

Câu 23:

23/07/2024

Đẳng thức nào sau đây đúng?

A. $\tan (180^{o} + a) = - \tan a$ .

B. $\cos (180^{o} + a) = - \cos a$ .

C. $\sin (180^{o} + a) = \sin a$ .

D. $\cot (180^{o} + a) = - \cot a$ .

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

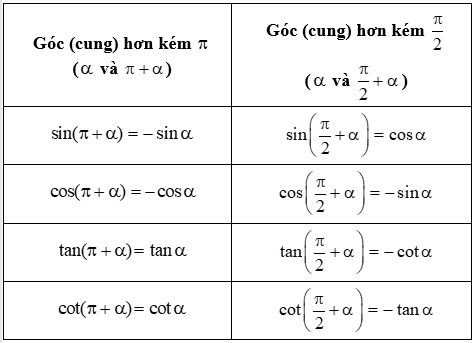
Lý thuyết “cung hơn kém $180^{°}$ ”

Câu 24:

23/07/2024

Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. $\sin (180^{°} - α) = - \sin α$ .

B. $\cos (180^{°} - α) = \cos α$

C. $\tan (180^{°} - α) = \tan α$ .

D. $\cot (180^{°} - α) = - \cot α$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Mối liên hệ hai cung bù nhau.

Câu 25:

23/07/2024

Cho

α

và

β

là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?

A. $\sin α = \sin β$ .

B. $\cos α = - \cos β$ .

C. $\tan α = - \tan β$ .

D. $\cot α = \cot β$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Mối liên hệ hai cung bù nhau.

Câu 26:

23/07/2024

Cho góc

α

tù. Điều khẳng định nào sau đây là đúng?

A. $\sin α < 0$ .

B. $\cos α > 0$ .

C. $\tan α > 0$ .

D. $\cot α < 0$ .

Xem đáp án

Đáp án: D

Câu 27:

23/07/2024

Điều khẳng định nào sau đây là đúng?

A. $\sin α = - \sin (180^{°} - α)$ .

B. $\cos α = - \cos (180^{°} - α)$ .

C. $\tan α = \tan (180^{°} - α)$ .

D. $c o t α = \cot (180^{°} - α)$ .

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Mối liên hệ hai cung bù nhau.

Câu 28:

23/07/2024

Hai góc nhọn

α

và

β

phụ nhau, hệ thức nào sau đây là sai?

A. $\sin α = \cos β$ .

B. $\tan α = \cot β$ .

C. $\cot β = \frac{1}{\cot α}$ .

D. $\cos α = - \sin β$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

$\cos α = \cos (90^{°} - β) = \sin β$

Câu 29:

23/10/2024

Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. $\sin 150^{°} = - \frac{\sqrt{3}}{2}$ .

B. $\cos 150^{°} = \frac{\sqrt{3}}{2}$ .

C. $\tan 150^{°} = - \frac{1}{\sqrt{3}}$ .

D.

\cot 150^{°} = \sqrt{3}

Xem đáp án

Đáp án đúng: C

*Phương pháp giải:

- căn cứ vào bảng giá trị lượng giác đặc biệt

*Lời giải:

Dựa vào bảng giá trị lượng giác đặc biệt ta có thể thấy được tan150 = -1/căn 3

vậy đáp án C đúng

*Một số dạng bài thêm về cung và góc lượng giác:

+ Bảng giá trị lượng giác của các góc đặc biệt

Dạng 2.1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

* Phương pháp giải: Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2.2: Chứng minh một đẳng thức giữa các giá trị lượng giác

* Phương pháp giải: Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 2.3: Rút gọn biểu thức lượng giác

* Phương pháp giải: Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo

Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án (Phần 2)

Giải Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Câu 30:

23/07/2024

Bất đẳng thức nào dưới đây là đúng?

A. $\sin 90^{°} < \sin 100^{°}$ .

B. $\cos 95^{°} > \cos 100^{°}$ .

C. $\tan 85^{°} < \tan 125^{°}$ .

D. $\cos 145^{°} > \cos 125^{°}$ .

Xem đáp án

Đáp án: B

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3