Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 3
Với giải bài tập Toán lớp 10 Bài tập cuối chương 3 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài tập cuối chương 3.
Giải bài tập Toán 10 Bài tập cuối chương 3
A. Trắc nghiệm
Bài 3.12 trang 44 Toán 10 Tập 1: Cho tam giác ABC có . Khẳng định nào sau đây là đúng?
D. b2 = c2 + a2 – 2ca.cos135o.
Lời giải:
Tam giác ABC có BC = a; AC = b; AB = c; .
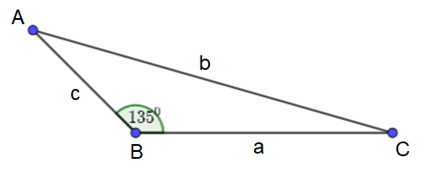
a) Diện tích tam giác ABC:
.
Chọn D.
b) Theo định lí sin, ta có:
A. sai vì
B.
Mà .
Do đó B đúng.
C. (loại vì không có dữ kiện về góc C nên không thể tính R theo c).
D. (loại vì không có dữ kiện về góc A nên không thể tính R theo a).
Chọn B.
c)
A. .
Vì theo định lí côsin, ta có: a2 = b2 + c2 − 2bc . cosA
Không đủ dữ kiện để suy ra: .
Do đó A sai.
B. .
Theo định lí sin, ta có:
Nên .
Do đó B sai.
C. .
Vì theo câu a, .
Do đó C sai.
D. b2 = c2 + a2 – 2ca . cos135o. đúng.
Theo định lý côsin ta có:
b2 = c2 + a2 − 2ca . cosB (*)
Mà cosB = cos 135o.
Thay vào (*) ta được: b2 = c2 + a2 − 2ca . cos 135o.
Do đó D đúng.
Chọn D.
Bài 3.13 trang 44 Toán 10 Tập 1: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
C. a2 = b2 + c2 + 2bc . cos A.
Lời giải:
a)
A.
Ta có . Mà r < R nên .
Do đó A sai.
B.
Ta có: S = pr .
Mà
.
Do đó B đúng.
C. a2 = b2 + c2 + 2bc . cos A.
Sai vì theo định lí côsin ta có: a2 = b2 + c2 − 2bc . cos A.
D. S = r(a + b + c).
Sai vì .
Chọn B.
b)
A. sinA = sin(B + C).
Ta có
sin(B + C) = sin(180° – ) = sin A.
Do đó, đáp án A đúng.
B. cos A = cos(B + C).
Sai vì cos (B + C) = cos(180° – ) = – cosA (do ).
C. cos A > 0.
∙ Nếu 0o < < 90o thì cos A > 0.
∙ Nếu 90o < < 180o thì cos A < 0.
Do đó C không đủ dữ kiện để kết luận.
D. sin A ≤ 0.
Ta có:
Mà b, c > 0 nên sin A > 0.
Do đó D sai.
Chọn D.
B. Tự luận
Bài 3.14 trang 44 Toán 10 Tập 1: Tính giá trị các biểu thức sau:
a) M = sin45o. cos45o + sin30o;
Lời giải:
a) M = sin45o. cos45o + sin30o
Ta có: sin 45o = cos 45o = ; sin 30o = .
Thay vào M, ta được:
M .
b)
Ta có: ; ; .
Thay vào N, ta được:
N = .
c) P = 1 + tan260o
Ta có: .
Thay vào P, ta được: P.
d)
Ta có: ;
Thay vào Q, ta được:
Q
Bài 3.15 trang 44 Toán 10 Tập 1: Cho tam giác ABC có AC = 10. Tính a, R, S, r.
Lời giải:
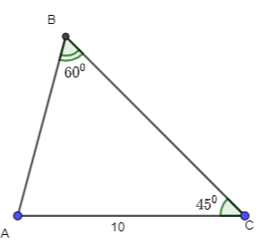
Theo định lí sin:
Ta có:
+ .
Mà b = AC = 10, .
Nên
.
+ a = 2R. sin A.
Mà , = 180o – 60o – 45o = 75o.
Nên a = 2.. sin 75o ≈ 11,15.
Diện tích tam giác ABC là:
(đvdt)
Khi đó:
+ .
+ .
+ .
Vậy a ≈ 11,15; , c ≈ 8,16, r ≈ 2,69.
Bài 3.16 trang 44 Toán 10 Tập 1: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
b) MA2 + MB2 – AB2 = 2MA.MB.cos và MA2 + MC2 – AC2 = 2MA.MC.cos;
c) (công thức đường trung tuyến).
Lời giải:
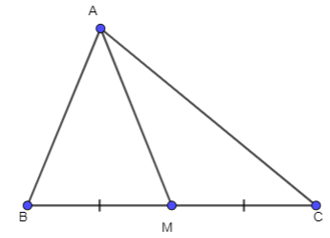
a) Ta có:
Vậy (đpcm)
b) Áp dụng định lí côsin trong ΔAMB, ta có:
AB2 = MA2 + MB2 – 2MA.MB.cos
MA2 + MB2 – AB2 = 2MA.MB.cos (1)
Áp dụng định lí côsin trong ΔAMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cos
MA2 + MC2 – AC2 = 2MA.MC.cos (2)
Từ (1) và (2) suy ra điều phải chứng minh.
c) Từ (1) suy ra: MA2 = AB2 – MB2 + 2MA.MB.cos
Từ (2) suy ra: MA2 = AC2 – MC2 + 2MA.MC.cos
Cộng vế với vế, ta được:
2MA2 = (AB2 – MB2 + 2MA.MB.cos) + (AC2 – MC2 + 2MA.MC.cos)
2MA2 = AB2 + AC2 – MB2 – MC2 + 2MA.MB.cos + 2MA.MC.cos
Mà (do AM là trung tuyến) nên:
2MA2 = AB2 + AC2 – – + 2MA.MB.cos + 2MA.MB.cos
2MA2 = AB2 + AC2 – + 2MA.MB.(cos + cos)
2MA2 = AB2 + AC2 –
(công thức đường trung tuyến).
Bài 3.17 trang 44 Toán 10 Tập 1: Cho tam giác ABC. Chứng minh rằng:
a) Nếu góc A nhọn thì b2 + c2 > a2;
b) Nếu góc A tù thì b2 + c2 < a2;
c) Nếu góc A vuông thì b2 + c2 = a2.
Lời giải:
Theo định lí côsin, ta có: a2 = b2 + c2 – 2bc.cosA
b2 + c2 – a2 = 2bc.cosA.
a) Nếu góc A nhọn thì cosA > 0 2bccosA > 0
Do đó: b2 + c2 – a2 = 2bc.cosA > 0.
Vậy b2 + c2 > a2 (đpcm).
b) Nếu góc A tù thì cosA < 0 2bccosA < 0
Do đó: b2 + c2 – a2 = 2bc.cosA < 0.
Vậy b2 + c2 < a2 (đpcm).
c) Nếu góc A vuông thì cosA = 0 2bccosA = 0
Do đó: b2 + c2 – a2 = 2bc.cosA = 0.
Vậy b2 + c2 = a2 (đpcm).
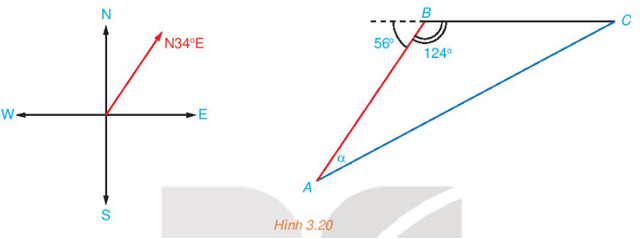
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A gặp tàu B?
Lời giải:
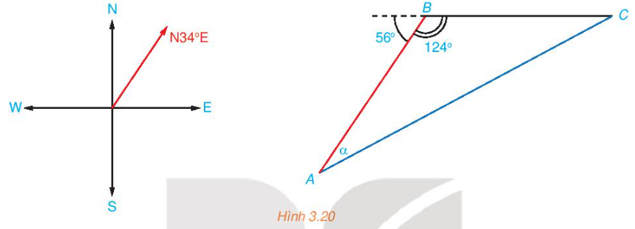
a) Gọi t (giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30 km/h nên quãng đường BC = 30t.
Tàu A đi với vận tốc có độ lớn 50 km/h nên quãng đường AC = 50t.
Theo định lí sin, ta có: .
Trong đó: a = BC = 30t, b = AC = 50t, , .
Khi đó,
α ≈ 30o hoặc α ≈ 150o (loại).
Do đó AC hợp với hướng bắc một góc 34o + 30o = 64o.
Vậy tàu A chuyển động theo hướng N64oE.
b) Xét tam giác ABC, ta có: .
.
Theo định lí sin, ta có:
Mà a = BC = 30t, c = AB = 53, .
Khi đó,
30t ≈ 60
t ≈ 2 (h)
Vậy sau 2 giờ thì tàu A gặp tàu B.
Lời giải:
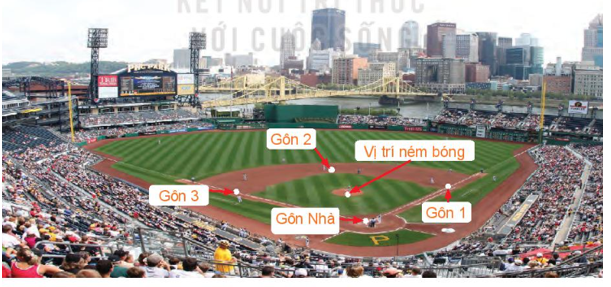
Kí hiệu gôn Nhà, gôn 1, gôn 2, gôn 3 và vị trí ném bóng lần lượt là các điểm A, B, C, D, O như hình vẽ.
Khi đó, tứ giác ABCD là hình vuông với đường chéo CA là tia phân giác của góc BCD. Hay .
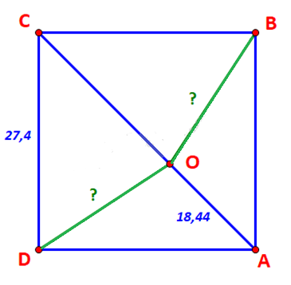
Ta có: CD = 27,4 AC = CD . = 27,4 . ≈ 38,75.
OC = AC – OA ≈ 38,75 − 18,44 = 20,31.
Xét tam giác OCD, áp dụng định lí côsin ta có:
OD2 = CD2 + CO2 – 2.CD.CO. cos.
Trong đó CD = 27,4; CO = 20,31;
Khi đó: OD2 = 27,42 + 20,312 – 2.27.20,31. cos 45o
OD2 ≈ 376,255
OD ≈ 19,4 (m)
Xét ΔCOB và ΔCOD, có:
BC = CD (ABCD là hình vuông)
(CA là tia phân giác của góc BCD)
Cạnh CO chung
Do đó ΔCOB = ΔCOD (c.g.c)
Suy ra OB = OD ≈ 19,4 (m) (hai cạnh tương ứng).
Vậy khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3 khoảng 19,4 m.
Lý thuyết Tổng hợp lý thuyết cuối chương 3
1. Giá trị lượng giác của một góc
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.
Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để .
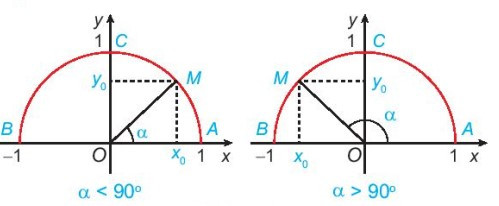
- Định nghĩa tỉ số lượng giác của một góc từ 00 đến 1800
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho . Khi đó:
+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;
+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;
+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là , được kí hiệu là tan α;
+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là , được kí hiệu là cot α.
- Từ định nghĩa trên ta có:
- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:
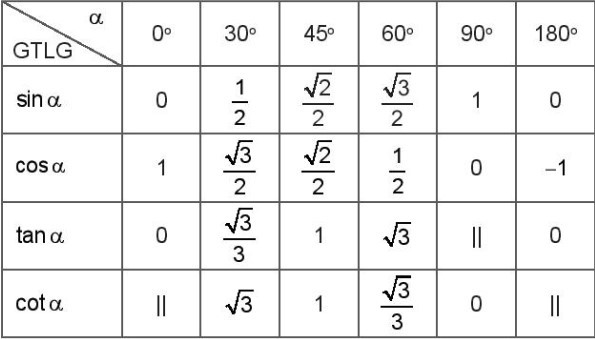
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.
Ví dụ: Tìm các giá trị lượng giác của góc 120°.
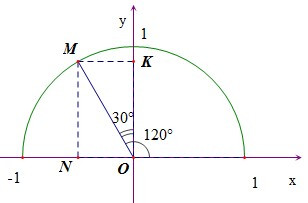
Gọi M là điểm trên nửa đường tròn đơn vị sao cho . Gọi N, K tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Do và nên và .
Từ bảng GTLG của một số góc đặc biệt:
Ta có: cos 600 = và cos 300 =
Các tam giác MOK và MON là các tam giác vuông với cạnh huyền bằng 1
Suy ra ON = cos.OM = cos600.1 = và OK = cos.OM = cos300.1 =
Mặt khác, do điểm M nằm bên trái trục tung nên
Theo định nghĩa giá trị lượng giác ta có:
sin 1200 =
cos 1200 =
tan 1200 =
cot 1200 = .
Vậy sin 1200 = ; cos 1200 = ; tan 1200 = ; cot 1200 = .
- Ta có thể dùng máy tính bỏ túi để tính giá trị gần đúng của các giá trị lượng giác của một góc.
Ví dụ:
 - Ta cũng có thể tìm được góc khi biết một giá trị lượng giác của góc đó.
- Ta cũng có thể tìm được góc khi biết một giá trị lượng giác của góc đó.
Ví dụ:
![]()
Chú ý:
+ Khi tìm x biết sin x, máy tính chỉ đưa ra giá trị x ≤ 90°.
+ Muốn tìm x khi biết cos x, tan x, ta cũng làm tương tự như trên, chỉ thay phím ![]() tương ứng bởi phím
tương ứng bởi phím ![]() .
.
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = - cos α;
tan (180° – α) = - tan α (α ≠ 90°);
cot (180° – α) = - cot α (0° < α < 180°).
Chú ý:
- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.
Ví dụ: Tính các giá trị lượng giác của góc 135°.
Hướng dẫn giải
Ta có 135° + 45° = 180°, vì vậy góc 135° và góc 45° là hai góc bù nhau:
Suy ra:
sin135° = sin45° =
cos135° = - cos45° =
tan135° = - tan45° = -1
cot135° = - cot45° = -1.
Vậy sin135° = ; cos135° = ; tan35° = -1 ; cot135° = -1.
- Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Ví dụ:
Ta có 30° + 60° = 90° nên góc 30° và góc 60° là hai góc phụ nhau.
Khi đó:
sin30° = cos60° =
tan30° = cot60° = .
3. Định lí côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
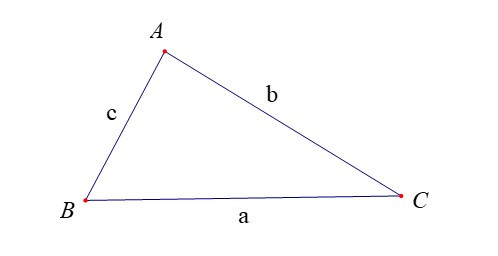
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Ví dụ: Cho tam giác ABC có góc A bằng 60° và AB = 2 cm, AC = 3 cm. Tính độ dài cạnh BC.
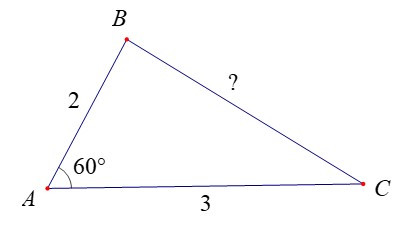
Hướng dẫn giải
Áp dụng Định lí côsin cho tam giác ABC, ta có:
BC2 = AB2 + AC2 – 2AB . AC . cos 600 = 22 + 32 – 2.2.3. = 7.
Suy ra BC = (cm)
Vậy BC = cm.
4. Định lí sin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Ví dụ: Cho tam giác ABC có góc A bằng 60° và AB = 2 cm, AC = 3 cm. Tính độ dài cạnh BC.
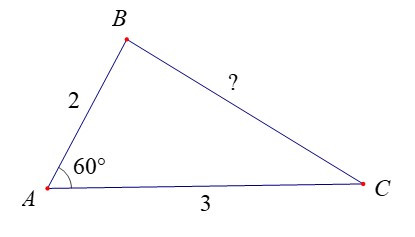
Hướng dẫn giải
Áp dụng Định lí côsin cho tam giác ABC, ta có:
BC2 = AB2 + AC2 – 2AB . AC . cos 600 = 22 + 32 – 2.2.3. = 7.
Suy ra BC = (cm)
Vậy BC = cm.
5. Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Ví dụ: Giải tam giác ABC biết b = 12, , .
Hướng dẫn giải
Theo định lí tổng ba góc của tam giác, ta có: .
Suy ra .
Áp dụng định lí sin, ta có:
Suy ra:
Vậy tam giác ABC có: , , ; a ≈ 34,6 ;b = 12; c ≈ 30,4.
Ví dụ: Để đo khoảng cách giữa hai đầu C và A của một hồ nước người ta không thể đi trực tiếp từ C đến A, người ta tiến hành như sau: Chọn 1 điểm B sao cho đo được khoảng cách BC, BA và góc BCA. Sau khi đo, ta nhận được BC = 5m, BA = 12m, . Tính khoảng cách AC (làm tròn kết quả đến hàng phần trăm).
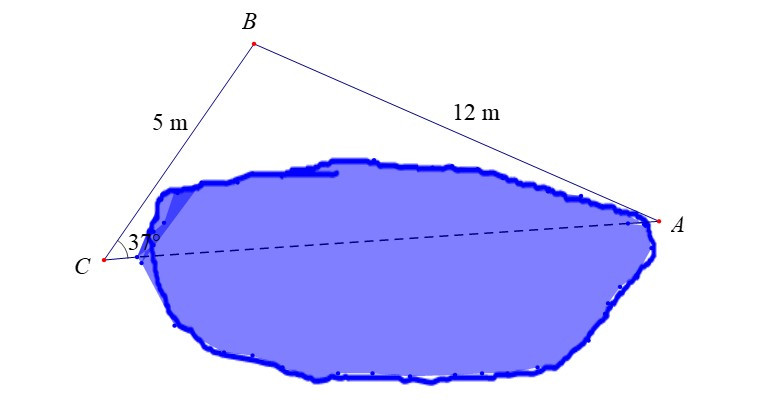
Hướng dẫn giải
Áp dụng định lí sin đối với tam giác ABC ta có:
⇒
⇒ sin A =
⇒ ≈ 14°31’
⇒ ≈ 180° – (37° + 14°31’) = 128°29’.
Áp dụng định lí sin, ta có:
⇒ AC = = ≈15,61 (m)
Vậy khoảng cách AC ≈ 15,61 m.
6. Công thức tính diện tích tam giác
Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Ta có các công thức tính diện tích tam giác ABC sau:
+) S = pr =
+) S = bc sin A = ca sin B =ab sin C.
+) S =
+) Công thức Heron: S = .
Ví dụ:
a) Tính diện tích tam giác ABC biết các cạnh b = 14 cm, c = 35 cm và .
b) Tính diện tích tam giác ABC và bán kính đường tròn nội tiếp, ngoại tiếp tam giác ABC, biết các cạnh a = 4 cm, b = 5 cm, c = 3 cm.
Hướng dẫn giải
a) Áp dụng công thức tính diện tích tam giác ABC, ta có:
S = bc sin A = .14.35.sin 60° = .14.35.=(cm2).
Vậy diện tích tam giác ABC là: cm2.
b) Ta có nửa chu vi của tam giác ABC là: (cm).
Áp dụng công thức Heron, ta có diện tích tam giác ABC là:
S =(cm2).
Mặt khác: S = ⇒ R = = (cm).
Ta có: S = pr ⇒ r = = = 1 (cm).
Vậy diện tích tam giác ABC là 6 cm2, bán kính đường tròn ngoại tiếp là 2,5 cm; bán kính đường tròn nội tiếp là 1 cm.
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vecto với một số
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 10 – Kết nối tri thức
- Soạn văn lớp 10 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 10 - KNTT
- Bố cục tác phẩm Ngữ văn lớp 10 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Kết nối tri thức
- Văn mẫu lớp 10 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 10 – Kết nối tri thức
- Giải sgk Tiếng Anh 10 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 10 Global Success – Kết nối tri thức
- Ngữ pháp Tiếng Anh 10 Global success
- Bài tập Tiếng Anh 10 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 10 Global success đầy đủ nhất
- Giải sgk Vật lí 10 – Kết nối tri thức
- Giải sbt Vật lí 10 – Kết nối tri thức
- Giải Chuyên đề Vật lí 10 – Kết nối tri thức
- Lý thuyết Vật lí 10 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 10 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 10 – Kết nối tri thức
- Lý thuyết Hóa học 10 – Kết nối tri thức
- Giải sbt Hóa học 10 – Kết nối tri thức
- Giải Chuyên đề Hóa học 10 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 10 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 10 – Kết nối tri thức
- Giải sbt Sinh học 10 – Kết nối tri thức
- Lý thuyết Sinh học 10 – Kết nối tri thức
- Giải Chuyên đề Sinh học 10 – Kết nối tri thức
- Giải sgk Lịch sử 10 – Kết nối tri thức
- Giải sbt Lịch sử 10 – Kết nối tri thức
- Giải Chuyên đề Lịch sử 10 – Kết nối tri thức
- Lý thuyết Lịch sử 10 - Kết nối tri thức
- Giải sgk Địa lí 10 – Kết nối tri thức
- Lý thuyết Địa Lí 10 – Kết nối tri thức
- Giải sbt Địa lí 10 – Kết nối tri thức
- Giải Chuyên đề Địa lí 10 – Kết nối tri thức
- Giải sgk Công nghệ 10 – Kết nối tri thức
- Lý thuyết Công nghệ 10 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Kết nối tri thức
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Kết nối tri thức
- Giải Chuyên đề Kinh tế và pháp luật 10 – Kết nối tri thức
- Lý thuyết KTPL 10 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 10 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 10 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 10 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm 10 – Kết nối tri thức
- Giải sgk Tin học 10 – Kết nối tri thức
- Lý thuyết Tin học 10 – Kết nối tri thức
- Giải sbt Tin học 10 – Kết nối tri thức
- Giải Chuyên đề Tin học 10 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 10 – Kết nối tri thức