Giải Toán 10 Bài 4 (Kết nối tri thức): Hệ bất phương trình bậc nhất hai ẩn

Giải bài tập Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn

Bài giảng Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn

Mở đầu

Mở đầu trang 26 Toán 10 Tập 1: Trong năm nay, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa: điều hòa hai chiều và điều hòa một chiều với số vốn ban đầu không vượt quá 1,2 tỉ đồng.

Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy để lợi nhuận thu được là lớn nhất?

Lời giải

Học xong bài này ta sẽ giải quyết bài toán như sau:

Gọi x, y (máy) lần lượt là số máy điều hòa hai chiều và số máy điều hòa một chiều mà chủ cửa hàng đầu tư $\left(x,y\in \mathbb{N}\right)$

Vì tổng số điều hòa hai chiều và một chiều không vượt quá 100 máy nên ta có bất phương trình: x + y ≤ 100

Đầu tư một máy điều hòa hai chiều là 20 triệu đồng và đầu tư một máy điều hòa một chiều là 10 triệu đồng nên số tiền đầu tư là: 20x + 10y (triệu đồng)

Vì số vốn ban đầu không vượt quá 1,2 tỉ đồng nên ta có bất phương trình:

20x + 10y ≤ 1 200

Lợi nhuận dự kiến chủ cửa hàng thu được là: F(x;y) = 3,5x + 2y (triệu đồng)

Bài toán trở thành tìm giá trị x, y thỏa mãn hệ bất phương trình: $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 100\\ 20x+10y\le 1200\end{array}\right.$ (1) để F(x;y) = 3,5x + 2y là lớn nhất.

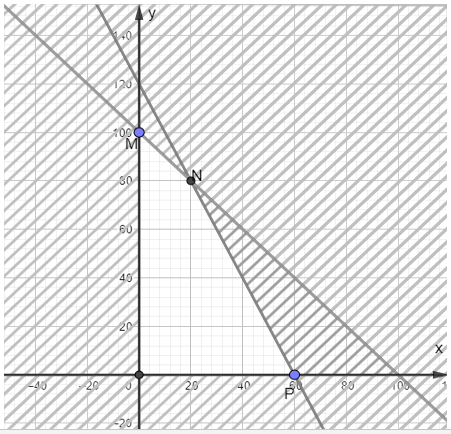
Biểu diễn miền nghiệm của hệ bất phương trình (1) trên mặt phẳng tọa độ bằng cách biểu diễn từng miền nghiệm của từng bất phương trình trong hệ bất phương trình (1), rồi lấy giao của các miền nghiệm ta được miền nghiệm của hệ BPT (1) là tứ giác OMNP với tọa độ các điểm O(0;0), M(0;100), N(20;80), P(60;0).

Tại O(0;0) giá trị biểu thức F(x;y) = 3,5x + 2y là: 3,5.0 + 2.0 = 0;

Tại M(0;100) giá trị biểu thức 3,5x + 2y là: 3,5.0 + 2.100 = 200;

Tại N(20;80) giá trị biểu thức 3,5x + 2y là: 3,5.20 + 2.80 = 230;

Tại P(60;0) giá trị biểu thức 3,5x + 2y là: 3,5.60 + 2.0 = 210;

Suy ra tại x = 20, y = 80 thì giá trị biểu thức 3,5x + 2y là lớn nhất.

Vậy nếu là chủ cửa hàng thì em cần đầu tư kinh doanh 20 cái điều hòa hai chiều, 80 cái điều hòa một chiều để lợi nhuận thu được là lớn nhất.

1. Hệ bất phương trình bậc nhất hai ẩn

Giải Toán 10 trang 26 Tập 1

HĐ 1 trang 26 Toán 10 Tập 1: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa hai chiều và một chiều mà cửa hàng cần nhập. Tính số tiền vốn cửa hàng phải bỏ ra để nhập hai loại máy điều hòa theo x và y.

a) Do nhu cầu của thị trường không quá 100 máy nên x và y cần thỏa mãn điều kiện gì?

b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên x và y phải thỏa mãn điều kiện gì?

c) Tính số tiền lãi mà chủ cửa hàng dự kiến thu được theo x và y.

Lời giải

Gọi số máy điều hòa hai chiều cần nhập là x; số máy điều hòa một chiều cần nhập là y $\left(x;y\in \mathbb{N}\right)$. Khi đó, số tiền để mua x điều hòa hai chiều là 20x và số tiền để mua y điều hòa một chiều là 10y .

Số tiền vốn cửa hàng phải bỏ ra là 20x + 10y (triệu đồng)

a) Do nhu cầu không quá 100 máy nên x + y ≤100.

b) Vì số vốn mà cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên x và y phải thỏa mãn bất phương trình 20x + 10y ≤ 1200 (triệu đồng).

c) Vì mỗi điều hòa hai chiều dự kiến lãi 3,5 triệu đồng/ máy và mỗi điều hòa một chiều dự kiến lãi 2 triệu đồng/máy nên số tiền lãi mà chủ cửa hàng dự kiến thu được theo x và y là: 3,5x + 2y (triệu đồng).

Giải Toán 10 trang 27 Tập 1

Luyện tập 1 trang 27 Toán 10 Tập 1: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa hai chiều, một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ bất phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.

Lời giải

Từ hoạt động 1 ta có hệ bất phương trình hai ẩn x; y như sau:

$\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 100\\ 20x+10y\le 1200\end{array}\right.$

Ta có:

x = 30; y = 40 ta có: 30 $\in \mathbb{N}$; 40$\in \mathbb{N}$

Ta có: 30 + 40 = 70 ≤ 100

20.30 + 10.40 = 1 000 < 1 200

Vậy một nghiệm của hệ bất phương trình là (30; 40).

2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

HĐ 2 trang 27 Toán 10 Tập 1: Cho đường thẳng d: x + y = 150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.

a) Xác định các miền nghiệm D₁, D₂, D₃ của các bất phương trình tương ứng x ≥ 0, y ≥ 0 và x + y ≤ 150.

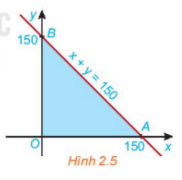
b) Miền tam giác OAB (H.2.5) có phải là giao của các miền nghiệm D₁, D₂, D₃ hay không?

c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:

$\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 150\end{array}\right.$

Lời giải

a)

+) Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0), tính cả Oy.

+) Miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1), tính cả Ox.

+) Xác định miền nghiệm D₃ của bất phương trình x + y ≤ 150.

- Vẽ đường thẳng d: x + y – 150 = 0.

- Vì 0 + 0 = 0 < 150 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 150

Do đó miền nghiệm D₃ của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ, kể cả đường thẳng d.

b) Giao điểm của ba miền nghiệm D₁, D₂, D₃ là miền tam giác OAB với O(0;0), A(150;0) và B(0;150)

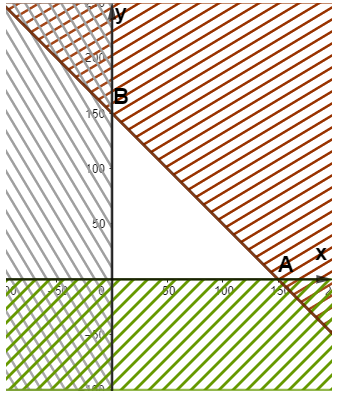
Do đó miền tam giác OAB (H.2.5) có là giao của các miền nghiệm D₁, D₂, D₃.

c) Điểm (1; 2) nằm trong tam giác OAB thỏa mãn x = 1 > 0, y = 2 > 0 và 1 + 2 = 3 < 150 nên cặp số (x; y) = (1;2) thỏa mãn cả ba bất phương trình của hệ bất phương trình đã cho. Do đó nó là một nghiệm của hệ bất phương trình đã cho.

Điểm (1;149) nằm trong tam giác OAB thỏa mãn x = 1 > 0, y = 149 > 0 và 1 + 149 = 150 ≤ 150 nên cặp số (x; y) = (1;149) thỏa mãn cả ba bất phương trình của hệ bất phương trình đã cho. Do đó nó là một nghiệm của hệ bất phương trình đã cho.

Giải Toán 10 trang 28 Tập 1

Luyện tập 2 trang 28 Toán 10 Tập 1: Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:

$\left\{\begin{array}{l}x\ge 0\\ y>0\\ x+y\le 100\\ 2x+y<120\end{array}\right.$

Lời giải

+) Xác định miền nghiệm D₁ của bất phương trình x$\ge$0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0), kể cả đường thẳng Oy.

+) Xác định miền nghiệm D₂ của bất phương trình y > 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1), không kể đường thẳng Ox.

+) Xác định miền nghiệm D₃ của bất phương trình x + y ≤ 100.

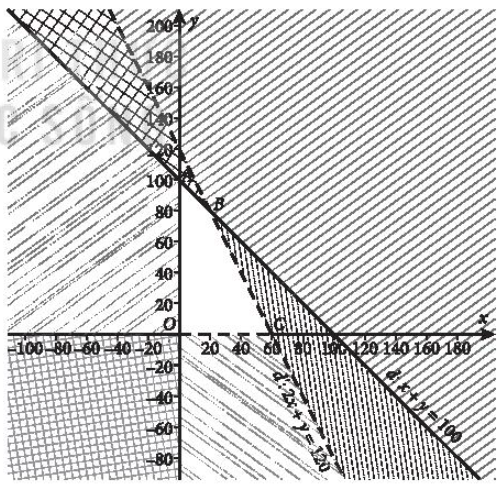
Ta vẽ đường thẳng x + y = 100 (d₁). Lấy điểm O(0; 0) thay tọa độ điểm này vào x + y ta được: 0 + 0 < 100. Vậy miền nghiệm D₃ là nửa mặt phẳng bờ d₁ chứa điểm O kể cả bờ là đường thẳng d₁.

+) Xác định miền nghiệm D₄ của bất phương trình 2x + y < 120

Ta vẽ đường thẳng 2x + y = 120 (d'). Lấy điểm O(0; 0) thay tọa độ điểm này vào 2x + y ta được: 2.0 + 0 < 120. Vậy miền nghiệm D₄ của bất phương trình là nửa mặt phẳng bờ d' chứa điểm O không kể bờ là đường thẳng d'_.

3.Ứng dụng của hệ bất phương trình bậc nhất hai ẩn

HĐ 3 trang 28 Toán 10 Tập 1: Xét biểu thức F(x; y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Tọa độ ba đỉnh là O(0;0), A(150; 0) và B(0; 150) (H.2.5).

a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.

b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.

c) Nêu nhận xét về tổng x + y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x; y) trên miền tam giác OAB.

Lời giải

a) O(0; 0); B(0; 150); A(150; 0).

Ta có: F(x; y) = 2x + 3y.

Khi đó ta tính được:

F(0; 0) = 2.0 + 3.0 = 0.

F(150; 0) = 2.150 + 3.0 = 300

F(0; 150) = 2.0 + 3.150 = 150

b) Trong miền tam giác OAB, lấy một điểm M(x; y) bất kì thì ta luôn có x $\ge$0; y$\ge$0 nên F(x; y) nhỏ nhất khi x = 0 và y = 0.

F(x; y) min = 2.0 + 3.0 = 0.

Vậy giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB là 0.

c) Vì điểm M(x; y) nằm trong miền tam giác OAB, nên tọa độ điểm M là nghiệm của bất phương trình x + y ≤ 150.

Hơn nữa, x ≥ 0, y ≥ 0 nên x + y ≥ 0.

Do đó ta có, 0 ≤ x + y ≤ 150 ⇔ 0 ≤ 2x + 2y ≤ 300

⇔ 0 + y ≤ 2x + 2y + y ≤ 300 + y

⇔ y ≤ 2x + 3y ≤ 300 + y (1)

Mà 0 ≤ y ≤ 150 nên 300 + y ≤ 300 + 150 = 450.

Từ (1) suy ra: 0 ≤ 2x + 3y ≤ 450 hay F(x; y) ≤ 450.

Dấu “=” xảy ra khi x + y = 150 và y = 150 hay x = 0 và y = 150.

Vậy F(x; y) đạt giá trị lớn nhất là 450 tại điểm B(0; 150).

Giải Toán 10 trang 30 Tập 1

Vận dụng trang 30 Toán 10 Tập 1: Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.

c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó để lợi nhuận thu được là lớn nhất.

Lời giải

a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) $\left(x,y\ge 0\right)$.

Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250

Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)

Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.

Ta có hệ bất phương trình: $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 250\\ x+2y\le 400\end{array}\right.$

Ta xác định miền nghiệm của hệ bất phương trình trên:

+) Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).

+) Miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).

+) Xác định miền nghiệm D₃ của bất phương trình x + y ≤ 250.

- Vẽ đường thẳng d: x + y = 250.

- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250

Do đó miền nghiệm D₃ của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.

+) Xác định miền nghiệm D₄ của bất phương trình x + 2y ≤ 400.

- Vẽ đường thẳng d’: x + 2y = 400.

- Vì 0 + 2 . 0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400

Do đó miền nghiệm D₄ của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.

Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với tọa độ các đỉnh là O(0;0), A(0; 200), B(100; 150), C(250; 0)

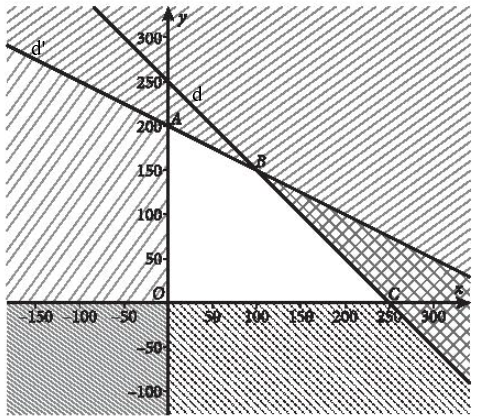
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).

Vậy F(x; y) = 2,5x + 4y.

c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 250\\ x+2y\le 400\end{array}\right.$.

Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.

Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;

Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;

Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;

Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.

Do đó F(x; y) lớn nhất bằng 850 tại x = 100 và y = 150.

Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

Bài tập

Bài 2.4 trang 30 Toán 10 Tập 1: Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

a) $\left\{\begin{array}{l}x<0\\ y\ge 0\end{array}\right.;$

b) $\left\{\begin{array}{l}x+y^2<0\\ y-x>1\end{array}\right.;$

c) $\left\{\begin{array}{l}x+y+z<0\\ y<0\end{array}\right.;$

d) $\left\{\begin{array}{l}-2x+y<3^2\\ 4^{2}x+3y<1\end{array}\right..$

Lời giải

a) $\left\{\begin{array}{l}x<0\\ y\ge 0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn.

Vì hệ $\left\{\begin{array}{l}x<0\\ y\ge 0\end{array}\right.$ gồm 2 bất phương trình x < 0 và y ≥ 0, đây đều là các bất phương trình bậc nhất hai ẩn (do x < 0 ⇔ 1x + 0y < 0 và y ≥ 0 ⇔ 0x + 1y ≥ 0).

b) $\left\{\begin{array}{l}x+y^2<0\\ y-x>1\end{array}\right.$ không phải là hệ bất phương trình bậc nhất hai ẩn vì x + y² < 0 không phải bất phương trình bậc nhất hai ẩn.

c) $\left\{\begin{array}{l}x+y+z<0\\ y<0\end{array}\right.$ không phải là hệ bất phương trình bậc nhất hai ẩn vì có bất phương trình x + y + z < 0 không phải bất phương trình bậc nhất hai ẩn.

d) $\left\{\begin{array}{l}-2x+y<3^2\\ 4^{2}x+3y<1\end{array}\right.\iff \left\{\begin{array}{l}-2x+y<9\\ 16x+3y<1\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn.

Bài 2.5 trang 30 Toán 10 Tập 1: Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:

a) $\left\{\begin{array}{l}y-x<-1\\ x>0\\ y<0\end{array}\right.;$

b) $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 2x+y\le 4\end{array}\right.;$

c) $\left\{\begin{array}{l}x\ge 0\\ x+y>5\\ x-y<0\end{array}\right..$

Lời giải

a) $\left\{\begin{array}{l}y-x<-1\\ x>0\\ y<0\end{array}\right.$

+) Xác định miền nghiệm D­₁ của bất phương trình y – x < – 1.

- Vẽ đường thẳng d: y – x = – 1.

- Vì 0 – 0 = 0 > – 1 nên tọa độ điểm (0; 0) không thỏa mãn bất phương trình y – x < – 1

Do đó miền nghiệm D₁ của bất phương trình y – x < – 1 là nửa mặt phẳng bờ d không chứa điểm O(0; 0) và không kể đường thẳng d.

+) Miền nghiệm D₂ của bất phương trình x > 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) và không kể đường thẳng Oy.

+) Miền nghiệm D₃ của bất phương trình y < 0 là nửa mặt phẳng bờ Ox chứ điểm (0; – 1) và không kể đường thẳng Ox.

Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

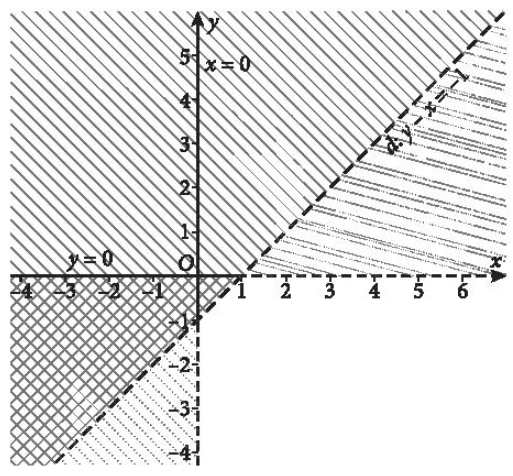
b) $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 2x+y\le 4\end{array}\right.$

Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) và kể cả đường thẳng Oy.

Miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) và kể cả đường thẳng Ox.

+) Xác định miền nghiệm D₃ của bất phương trình 2x + y ≤ 4.

– Vẽ đường thẳng d: 2x + y = 4

- Vì 2.0 + 0 = 0 < 4 nên tọa độ điểm (0; 0) thỏa mãn bất phương trình 2x + y ≤ 4

Do đó miền nghiệm D₃ của bất phương trình 2x + y ≤ 4 là nửa mặt phẳng bờ d chứa điểm O(0; 0) và kể cả đường thẳng d.

Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (miền không bị gạch).

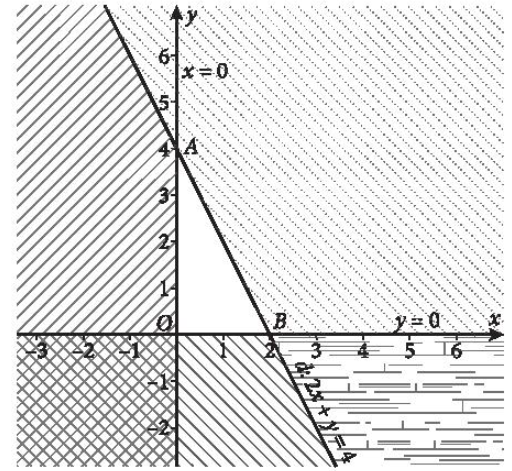
c) $\left\{\begin{array}{l}x\ge 0\\ x+y>5\\ x-y<0\end{array}\right..$

Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) và kể cả đường thẳng Oy.

+) Xác định miền nghiệm D₂ của bất phương trình x + y > 5.

– Vẽ đường thẳng d: x + y = 5

- Vì 0 + 0 = 0 < 5 nên tọa độ điểm (0; 0) không thỏa mãn bất phương trình x + y > 5

Do đó miền nghiệm D₂ của bất phương trình x + y > 5 là nửa mặt phẳng bờ d không chứa điểm O(0; 0) và không kể đường thẳng d.

+) Xác định miền nghiệm D₃ của bất phương trình x – y < 0.

– Vẽ đường thẳng d’: x – y = 0

- Vì 1 - 0 = 1 > 0 nên tọa độ điểm (1; 0) không thỏa mãn bất phương trình x – y < 0

Do đó miền nghiệm D₃ của bất phương trình x – y < 0 là nửa mặt phẳng bờ d’ không chứa điểm (1; 0) và không kể đường thẳng d’.

Vậy miền nghiệm của hệ là miền không bị gạch.

Bài 2.6 trang 30 Toán 10 Tập 1: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipid trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipid. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipid. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 250 nghìn đồng; 1kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

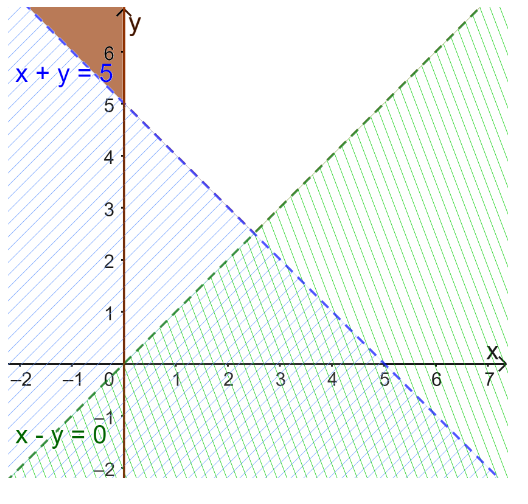
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Lời giải

Số kilôgam thịt bò gia đình mua là x (kg); số kilôgam thịt lợn gia đình mua là y (kg). Vì số kilôgam thịt bò mua nhiều nhất là 1,6 kg và số kilôgam thịt lợn mua nhiều nhất là 1,1 kg nên ta có:

$0\le x\le 1,6;0\le y\le 1,1$ (1)

Vì mỗi kilôgam thịt bò có chứa 800 đơn vị protein và mỗi kilôgam thịt lợn có chứa 600 đơn vị protein nên khối lượng protein có trong x kg thịt bò và y kg thịt lợn là: 800x + 600y (đơn vị).

Mà mỗi ngày gia đình cần ít nhất 900 đơn vị protein nên ta có bất phương trình:

800x + 600y ≥ 900 (2)

Vì mỗi kilôgam thịt bò có chứa 200 đơn vị lipid và mỗi kilôgam thịt lợn có chứa 400 đơn vị lipid nên khối lượng lipid có trong x kg thịt bò và y kg thịt lợn là: 200x + 400y (đơn vị).

Mà mỗi ngày gia đình cần ít nhất 400 đơn vị lipid nên ta có bất phương trình:

200x + 400y ≥ 400 (3)

Từ (1); (2); (3) ta có hệ bất phương trình:

$\left\{\begin{array}{l}0\le x\le 1,6\\ 0\le y\le 1,1\\ 800x+600y\ge 900\\ 200x+400y\ge 400\end{array}\right.$$\iff \left\{\begin{array}{l}0\le x\le 1,6\\ 0\le y\le 1,1\\ 8x+6y\ge 9\\ x+2y\ge 2\end{array}\right.$

Ta đi xác định miền nghiệm của hệ bất phương trình.

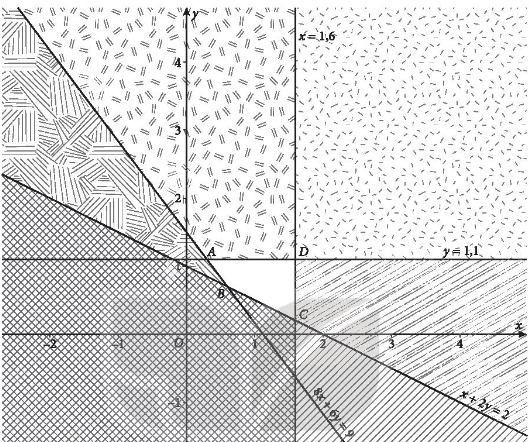
Miền nghiệm của hệ bất phương trình là tứ giác ABCD có trong hình vẽ trên với tọa độ các đỉnh là A(0,3; 1,1), B(0,6; 0,7), C(1,6; 0,2), D(1,6; 1,1).

b) Số tiền mua một kilôgam thịt bò là 250 nghìn đồng và số tiền mua một kilôgam thịt lợn là 160 nghìn đồng nên số tiền để mua x kg thịt bò và y kg thịt lợn là: F(x; y) = 250x + 160y (nghìn đồng).

c) Người ta đã chứng minh được để số tiền mua ít nhất thì (x; y) là tọa độ của một trong bốn đỉnh tứ giác ABCD.

Ta có: F(x; y) = 250x + 160y. Khi đó:

F(0,3; 1,1) = 250 . 0,3 + 160 . 1,1 = 251;

F(0,6; 0,7) = 250 . 0,6 + 160 . 0,7 = 262;

F(1,6; 0,2) = 250 . 1,6 + 160 . 0,2 = 432;

F(1,6; 1,1) = 250 . 1,6 + 160 . 1,1 = 576;

Suy ra giá trị nhỏ nhất cần tìm là F(0,3; 1,1) = 251.

Vậy để chi phí là ít nhất thì gia đình cần mua 0,3 kilôgam thịt bò và 1,1 kilôgam thịt lợn.

Lý thuyết Hệ bất phương trình bậc nhất hai ẩn

1. Hệ bất phương trình bậc nhất hai ẩn

- Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.

- Cặp số $\left({\mathrm{x}}_0;{\mathrm{y}}_0\right)$ là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi $\left({\mathrm{x}}_0;{\mathrm{y}}_0\right)$ đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.

Ví dụ:

$\left\{\begin{array}{l}\mathrm{x}+2\mathrm{y}<9\\ \mathrm{y}-2\mathrm{x}>9\end{array}\right.$là một hệ bất phương trình hai ẩn gồm 2 bất phương trình $\mathrm{x}+2\mathrm{y}<9$ và $\mathrm{y}-2\mathrm{x}>9$.

$\left\{\begin{array}{l}{\mathrm{x}}^2+{\mathrm{y}}^2<5\\ \mathrm{x}-\mathrm{y}>4\end{array}\right.$ không phải là hệ bất phương trình bậc nhất hai ẩn bởi ${\mathrm{x}}^2+{\mathrm{y}}^2<5$ là bất phương trình bậc hai 2 ẩn.

- Cho hệ bất phương trình hai ẩn $\left\{\begin{array}{l}\mathrm{x}+\mathrm{y}>9\\ \mathrm{x}-\mathrm{y}<9\end{array}\right.$.

Cặp (x; y) = (10; 2) là nghiệm của bất phương trình x + y > 9 và cũng là nghiệm của bất phương trình x – y < 9. Nên cặp (x; y) = (10; 2) là nghiệm của hệ bất phương trình trên.

2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Ví dụ: Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn:$\left\{\begin{array}{l}\mathrm{x}\ge 0\\ \mathrm{y}\ge 0\\ \mathrm{x}+\mathrm{y}\le 150\end{array}\right.$:

Bước 1: Xác định miền nghiệm D₁ của bất phương trình x ≥ 0 và gạch bỏ phần miền còn lại.

- Đường thẳng x = 0 là trục tọa độ Oy.

- Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.

Bước 2: Tương tự, miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.

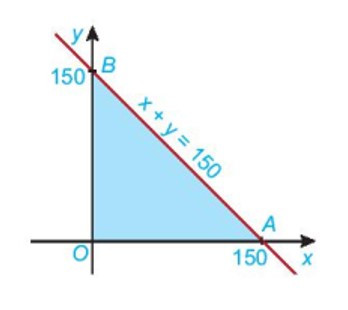
Bước 3: Miền nghiệm D₃ của bất phương trình x + y ≤ 150:

- Vẽ đường thẳng d: x + y = 150.

- Vì 0 + 0 ≤ 150 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 150.

Do đó, miền nghiệm D₃ của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ O.

Từ đó ta có miền nghiệm tô màu xanh chính là giao miền nghiệm của các bất phương trình trong hệ.

3. Ứng dụng của hệ bất phương trình bậc nhất hai ẩn

Nhận xét: Tổng quát, người ta chứng minh được rằng giá trị lớn nhất (hay nhỏ nhất) của biểu thức $\mathrm{F}\left(\mathrm{x};\mathrm{y}\right)=\mathrm{ax}+\mathrm{by}$, với $\left(\mathrm{x};\mathrm{y}\right)$ là tọa độ các điểm thuộc miền đa giác ${\mathrm{A}}_1{\mathrm{A}}_2\mathrm{...}{\mathrm{A}}_{\mathrm{n}}$, tức là các điểm nằm bên trong hay nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.

Ví dụ: Cho hệ bất phương trình bậc nhất hai ẩn: $\left\{\begin{array}{l}\mathrm{x}\ge 0\\ \mathrm{y}\ge 0\\ \mathrm{x}+\mathrm{y}\le 100\\ 2\mathrm{x}+\mathrm{y}\le 120\end{array}\right.$và $\mathrm{F}\left(\mathrm{x};\mathrm{y}\right)=3,5\mathrm{x}+2\mathrm{y}$. Tìm giá trị lớn nhất của $\mathrm{F}\left(\mathrm{x};\mathrm{y}\right)$.

Hướng dẫn giải:

Bước 1: Xác định miền nghiệm của hệ bất phương trình trên.

- Xác định miền nghiệm D₁ của bất phương trình x ≥ 0.

- Đường thẳng x = 0 là trục tọa độ Oy.

- Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.

- Tương tự, miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.

- Miền nghiệm D₃ của bất phương trình x + y ≤ 100:

+ Vẽ đường thẳng d₁: x + y = 100.

+ Vì 0 + 0 ≤ 100 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 100.

Do đó, miền nghiệm D₃ của bất phương trình x + y ≤ 100 là nửa mặt phẳng bờ d₁ chứa gốc tọa độ O.

- Miền nghiệm D₄ của bất phương trình 2x + y ≤ 120:

+ Vẽ đường thẳng d₂: 2x + y = 120.

+ Vì 2. 0 + 0 ≤ 120 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình 2x + y ≤ 120.

Do đó, miền nghiệm D₄ của bất phương trình 2x + y ≤ 120 là nửa mặt phẳng bờ d₂ chứa gốc tọa độ O.

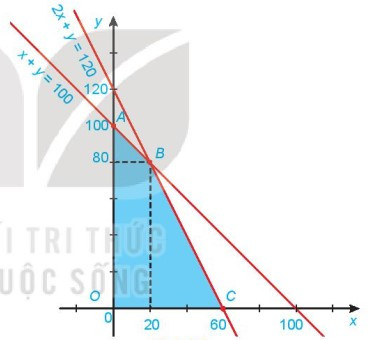
Từ đó ta có miền nghiệm tô màu xanh chính là giao miền nghiệm của các bất phương trình trong hệ.

Miền nghiệm là miền tứ giác OABC với O(0;0), A(0;100), B(20;80) và C(60;0).

Bước 2: Tính giá trị của biểu thức F tại các đỉnh của tứ giác

F(O) = 0; F(A) = 200; F(B) = 230; F(C) = 210.

Bước 3: So sánh các giá trị thu được ở Bước 2, kết luận giá trị lớn nhất của $\mathrm{F}\left(\mathrm{x};\mathrm{y}\right)$ là 230.

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài ôn tập chương 2

Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 6: Hệ thức lượng trong tam giác

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Xem thêm tài liệu Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Lý thuyết Bài 4. Hệ bất phương trình bậc nhất hai ẩn

Trắc nghiệm Bài 4: Hệ bất phương trình bậc nhất hai ẩn