Giải Toán 10 (Kết nối tri thức): Bài tập cuối chương 9

Giải bài tập Toán 10 Bài tập cuối chương 9

A. Trắc nghiệm

Giải Toán 10 trang 88 Tập 2

Bài tập 9.13 trang 88 Toán 10 Tập 2: Một hộp có bốn loại bi: bi xanh, bi đỏ, bi trắng và bi vàng. Lấy ngẫu nhiên ra một viên bi. Gọi E là biến cố: “Lấy được viên bi đỏ”. Biến cố đối của E là biến cố

A. Lấy được viên bi xanh.

B. Lấy được viên bi vàng hoặc bi trắng.

C. Lấy được viên bi trắng.

D. Lấy được viên bi vàng hoặc bi trắng hoặc bi xanh.

Lời giải

Đáp án D

Phép thử lấy ngẫu nhiên một viên bi từ hộp có bốn loại bi: bi xanh, bi đỏ, bi trắng và bi vàng.

Xét biến cố E: “Lấy được viên bi đỏ”:

Nếu E không xảy ra, tức là không lấy được bị màu đỏ thì sẽ lấy được bi màu xanh hoặc màu trắng hoặc màu vàng.

Do đó biến cố đối của E là “Lấy được viên bi vàng hoặc bi trắng hoặc bi xanh”.

Vậy ta chọn đáp án D.

Bài tập 9.14 trang 88 Toán 10 Tập 2: Rút ngẫu nhiên ra một thẻ từ một hộp có 30 tấm thẻ được đánh số từ 1 đến 30. Xác suất để số trên tấm thẻ được rút ra chia hết cho 5 là:

A. $\frac{1}{30}$.

B. $\frac{1}{5}$.

C. $\frac{1}{3}$.

D. $\frac{2}{5}$.

Lời giải

Đáp án B

Rút ngẫu nhiên ra một thẻ từ một hộp có 30 tấm thẻ được đánh số từ 1 đến 30 thì không gian mẫu Ω = {1; 2; 3; …; 29; 30}.

⇒ n(Ω) = 30.

Gọi biến cố A: “số trên tấm thẻ được rút ra chia hết cho 5”

Khi đó A = {5; 10; 15; 20; 25; 30}.

⇒ n(A) = 6

⇒ $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{6}{30}=\frac{1}{5}$.

Vậy ta chọn đáp án B.

Bài tập 9.15 trang 88 Toán 10 Tập 2: Gieo hai con xúc xắc cân đối. Xác suất để tổng số chấm xuất hiện trên hai con xúc xắc không lớn hơn 4 là:

A. $\frac{1}{7}$.

B. $\frac{1}{6}$.

C. $\frac{1}{8}$.

D. $\frac{2}{9}$.

Lời giải

Đáp án B

Do gieo một con xúc xắc thì số chấm xuất hiện có thể là 1, 2, 3, 4, 5, 6 nên khi gieo 2 con xúc xắc thì các kết quả của không gian mẫu được cho trong bảng:

Từ bảng trên, mỗi ô tương ứng với một kết quả có thể. Có 36 ô, vậy n(Ω) = 36.

a) Gọi biến cố A: “tổng số chấm xuất hiện trên hai con xúc xắc không lớn hơn 4”.

Khi đó A = {(1; 1), (1; 2), (1; 3), (2; 1), (2; 2), (3; 1)}

⇒ n(A) = 6. Khi đó $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{6}{36}=\frac{1}{6}$.

Vậy xác suất để “tổng số chấm xuất hiện trên hai con xúc xắc không lớn hơn 4” là $\frac{1}{6}$.

Vậy ta chọn đáp án B.

Bài tập 9.16 trang 88 Toán 10 Tập 2: Một tổ trong lớp 10T có 4 bạn nữ và 3 bạn nam. Giáo viên chọn ngẫu nhiên hai bạn trong tổ đó tham gia đội làm báo của lớp. Xác suất để hai bạn được chọn có một bạn nam và một bạn nữ là

A. $\frac{4}{7}$.

B. $\frac{2}{7}$.

C. $\frac{1}{6}$.

D. $\frac{2}{21}$.

Lời giải

Đáp án A

Vì tổ có 4 bạn nữ và 3 bạn nam nên tổ đó có 4 + 3 = 7 (học sinh).

Chọn 2 trong 7 bạn học sinh của tổ đó, ta có $C_7^2$ = 21(cách chọn).

Gọi A là biến cố “hai bạn được chọn có một bạn nam và một bạn nữ”.

+ Để chọn được 1 bạn nữ trong 4 bạn nữ, ta có $C_4^1$ = 4 (cách chọn).

+ Để chọn được 1 bạn nam trong 3 bạn nam, ta có $C_3^1$ = 3 (cách chọn).

Áp dụng quy tắc nhân ta có 4.3 = 12 cách chọn 1 bạn nữ và 1 bạn nam.

Suy ra n(A) = 12.

Khi đó $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{12}{21}=\frac{4}{7}$.

Vậy xác suất để hai bạn được chọn có một bạn nam và một bạn nữ là $\frac{4}{7}$.

Do đó, ta chọn đáp án A.

B. Tự luận

Bài tập 9.17 trang 88 Toán 10 Tập 2: Một hộp đựng bảy thẻ màu xanh đánh số từ 1 đến 7; năm thẻ màu đỏ đánh số từ 1 đến 5 và hai thẻ màu vàng đánh số từ 1 đến 2 . Rút ngẫu nhiên ra một tấm thẻ.

a) Mô tả không gian mẫu.

b) Mỗi biến cố sau là tập con nào của không gian mẫu?

A: “Rút ra được thẻ màu đỏ hoặc màu vàng”;

B: “Rút ra được thẻ mang số hoặc là 2 hoặc là 3”.

Lời giải

a) Gọi X, Đ, V lần lượt là thẻ màu xanh, đỏ, vàng; 1, 2, 3, 4, 5, 6, 7 lần lượt là số được đánh trên thẻ.

Khi rút ngẫu nhiên ra một thẻ thì ta có không gian mẫu: Ω = {X1; X2; X3; X4; X5; X6; X7; Đ1; Đ2; Đ3; Đ4; Đ5; V1; V2}

⇒ n(Ω) = 14.

b) Xét biến cố A: “Rút ra được thẻ màu đỏ hoặc màu vàng”.

Khi đó A= { Đ1; Đ2; Đ3; Đ4; Đ5; V1; V2} ⊂ Ω.

Xét biến cố B: “Rút ra được thẻ mang số hoặc là 2 hoặc là 3”.

Khi đó B = { X2; X3; Đ2; Đ3; V2}⊂ Ω.

Vậy A= { Đ1; Đ2; Đ3; Đ4; Đ5; V1; V2} và B = { X2; X3; Đ2; Đ3; V2}.

Bài tập 9.18 trang 88 Toán 10 Tập 2: Có hộp I và hộp II, mỗi hộp chứa 5 tấm thẻ đánh số từ 1 đến 5. Từ mỗi hộp, rút ngẫu nhiên ra một tấm thẻ. Tính xác suất để thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I.

Lời giải

Gọi 1, 2, 3, 4, 5 lần lượt là tấm thẻ có đánh số tương ứng.

Từ mỗi hộp rút ngẫu nhiên ra một tấm thẻ, khi đó ta có bảng các kết quả có thể sau:

Trong bản có 25 ô tương ứng với 25 kết quả có thể. Do đó n(Ω) = 25.

Gọi biến cố A: “Thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I”.

⇒ A = {(1;2), (1;3), (1;4), (1;5); (2;3); (2;4); (2;5); (3;4); (3;5); (4;5)}.

⇒ n(A) = 10

⇒ $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{10}{25}=\frac{2}{5}$.

Vậy xác suất để thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I là $\frac{2}{5}$.

Bài tập 9.19 trang 88 Toán 10 Tập 2: Gieo đồng thời hai con xúc xắc cân đối. Tính xác suất để:

a) Tổng số chấm trên hai con xúc xắc bằng 8;

b) Tồng số chấm trên hai con xúc xắc nhỏ hơn 8.

Lời giải

Do gieo một con xúc xắc thì số chấm xuất hiện có thể là 1, 2, 3, 4, 5, 6 nên khi gieo 2 con xúc xắc thì các kết quả của không gian mẫu được cho trong bảng:

Từ bảng trên, mỗi ô tương ứng với một kết quả có thể. Có 36 ô, vậy n(Ω) = 36.

a) Gọi biến cố A: “Tổng số chấm trên hai con xúc xắc bằng 8”.

Khi đó A = {(2; 6), (3; 5), (4; 4), (5; 3), (6; 2)}.

⇒ n(A) = 5.

Khi đó $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{5}{36}$.

Vậy xác suất để “Tổng số chấm trên hai con xúc xắc bằng 8” là $\frac{5}{36}$.

b) Gọi biến cố B: “Tổng số chấm trên hai con xúc xắc nhỏ hơn 8”.

Khi đó B = {(1;1), (1;2), (1;3), (1;4), (1;5), (1;6), (2;1), (2;2), (2;3), (2;4), (2;5), (3;1), (3;2), (3;3), (3;4), (4;1), (4;2), (4;3), (5;1), (5;2), (6;1)}

⇒ n(B) = 21.

Khi đó $P\left(B\right)=\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{21}{36}=\frac{7}{12}$.

Vậy xác suất để “Tổng số chấm trên hai con xúc xắc nhỏ hơn 8” là $\frac{7}{12}$.

Giải Toán 10 trang 89 Tập 2

Bài tập 9.20 trang 89 Toán 10 Tập 2: Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất của các biến cố:

F: “Trong ba ngày, có đúng một ngày có mưa”;

G: “Trong ba ngày, có ít nhất hai ngày không mưa”.

Lời giải

a) Kí hiệu M là mưa, K là không mưa.

Khi đó ta có sơ đồ cây mô tả không gian mẫu như sau:

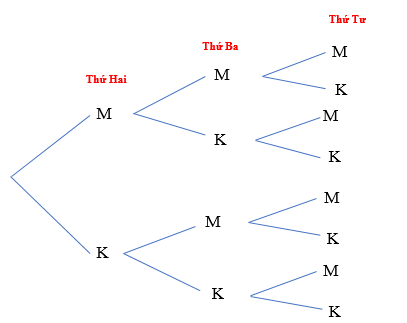
Từ sơ đồ hình cây ta thấy có những kết quả có thể là: MMM; MMK; MKM; MKK; KMM; KMK; KKM; KKK.

⇒ Ω = {MMM; MMK; MKM; MKK; KMM; KMK; KKM; KKK}.

⇒ n(Ω) = 8.

b) Xét biến cố F: “Trong ba ngày, có đúng một ngày có mưa”.

Khi đó F = { MKK; KMK; KKM}.

⇒ n(F) = 3.

⇒ $P\left(F\right)=\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{3}{8}$.

Xét biến cố G: “Trong ba ngày, có ít nhất hai ngày không mưa”.

G = { MKK; KMK; KKM; KKK}.

⇒ n(G) = 4

⇒ $P\left(G\right)=\frac{n\left(G\right)}{n\left(\Omega \right)}=\frac{4}{8}=\mathrm{0,5}$.

Vậy P(F) = $\frac{3}{8}$ và P(G) = 0,5.

Bài tập 9.21 trang 89 Toán 10 Tập 2: Gieo một đồng xu cân đối liên tiếp bốn lần.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.

Lời giải

a) Kí hiệu S là mặt sấp, N là mặt ngửa. Mỗi lần gieo đồng xu có thể là mặt sấp hoặc mặt ngửa xuất hiện.

Do đó, ta có sơ đồ cây mô tả không gian mẫu như sau:

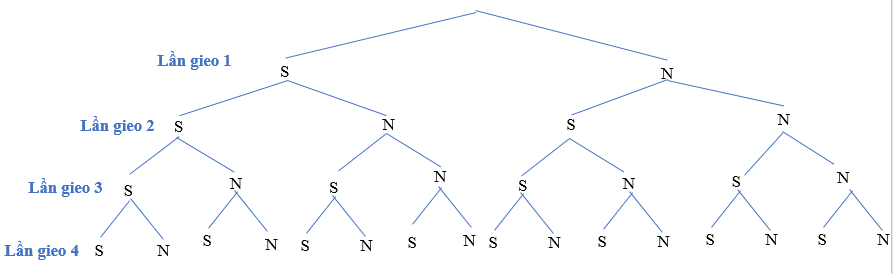
Từ sơ đồ cây ta thấy có các kết quả có thể là :

Ω = {SSSS; SSSN ; SSNS ; SSNN ; SNSS; SNSN; SNNS; SNNN; NSSS; NSSN; NSNS; NSNN; NNSS; NNSN; NNNS; NNNN}.

⇒ n(Ω) = 16.

b) Xét biến cố A: “Trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”

A = {SSNN ; SNSN; SNNS; NSSN; NSNS; NNSS }.

⇒ n(A) = 6.

⇒ $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{6}{16}=\frac{3}{8}$.

Vậy xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa là $\frac{3}{8}$.

Bài tập 9.22 trang 89 Toán 10 Tập 2: Chọn ngẫu nhiên 4 viên bi từ một túi đựng 4 viên bi đỏ và 6 viên bi xanh đôi một khác nhau. Gọi A là biến cố: “Trong bốn viên bi đó có cả bi đỏ và cả bi xanh”. Tính P(A) và P($\overline{A}$).

Lời giải

Có 4 viên bi đỏ và 6 viên bi xanh thì có tất cả 4 + 6 = 10 viên bi.

Chọn 4 viên bi từ 10 viên bi, thì số cách là: $C_{10}^4$ = 210 (cách).

⇒ n(Ω) = 210.

Xét biến cố A:“Trong bốn viên bi đó có cả bi đỏ và cả bi xanh”.

Khi đó nếu biến cố A không xảy ra tức là: trong bốn viên bi đó không có cả bi đỏ và cả bi xanh hay trong bốn viên bi chỉ có bi đỏ hoặc chỉ có bi xanh.

Khi đó $\overline{A}$: “trong bốn viên bi chỉ có bi đỏ hoặc chỉ có bi xanh”.

- Trường hợp 1: Cả 4 viên bi đều màu đỏ, có $C_4^4$ = 1 cách chọn.

- Trường hợp 2: Cả 4 viên bi đều màu xanh, có $C_6^4$ = 15 cách chọn.

Áp dụng quy tắc cộng ta có số cách chọn là 1 + 15 = 16 (cách).

Suy ra n ($\overline{A}$) = 16.

⇒ $P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{16}{210}=\frac{8}{105}$.

Mặt khác P($\overline{A}$) = 1 – P(A)

⇒ P(A) = 1 – P($\overline{A}$) = 1–$\frac{8}{105}$ = $\frac{97}{105}$.

Vậy P(A) = $\frac{97}{105}$ và P($\overline{A}$) = $\frac{8}{105}$.

Lý thuyết tổng hợp Toán 10 Chương 9

1. Biến cố

- Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà kết quả của nó không thể biết được trước khi phép thử được thực hiện.

- Không gian mẫu của phép thử là tập hợp tất cả các kết quả có thể xảy ra khi thực hiện phép thử. Không gian mẫu của phép thử được kí hiệu là Ω.

- Kết quả thuận lợi cho một biến cố E liên quan tới phép thử T là kết quả của phép thử T làm cho biến cố đó xảy ra.

Chú ý: Ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn kết quả.

Ví dụ: Trong một túi gồm ba quả bóng: màu đỏ, màu xanh, màu vàng. Lấy ngẫu nhiên ra một quả bóng. Phép thử ngẫu nhiên ở đây là gì? Mô tả không gian mẫu.

Hướng dẫn giải

Phép thử ngẫu nhiên ở đây là lấy ngẫu nhiên một quả bóng trong túi.

Khi lấy ngẫu nhiên ra một quả bóng thì có các kết quả có thể là: lấy được quả bóng màu đỏ hoặc quả bóng màu xanh, hoặc quả bóng màu vàng.

Vậy không gian mẫu là Ω = {bóng màu đỏ, bóng màu xanh, bóng màu vàng}.

- Mỗi biến cố là một tập con của không gian mẫu Ω. Tập con này là tập hợp tất cả các kết quả thuận lợi cho biến cố đó.

- Biến cố chắc chắn là tập Ω, biến cố không thể là tập ∅.

- Biến cố đối của biến cố E là biến cố “E không xảy ra”.

Biến cố đối của E được kí hiệu là $\overline{E}$.

Nhận xét: Nếu biến cố E là tập con của không gian mẫu Ω thì biến cố đối $\overline{E}$ là tập hợp tất cả cá phần tử của Ω mà không là phần tử của E. Vậy biến cố $\overline{E}$ là phần bù của E trong Ω: $\overline{E}$ = C_ΩE.

Ví dụ: Gieo một con xúc xắc cân đối, đồng chất.

a) Không gian mẫu ở đây là gì?

b) Gọi A là biến cố “Số chấm xuất hiện là số lẻ”. Biến cố A là tập con nào của không gian mẫu.

c) Tìm biến cố đối của biến cố A.

Hướng dẫn giải

a) Khi gieo con xúc xắc cân đối, đồng chất thì có 6 khả năng có thể xảy ra, đó là xuất hiện mặt 1, 2, 3, 4, 5, 6 (chấm).

⇒ Không gian mẫu của phép thử là Ω = {1; 2; 3; 4; 5; 6}.

Vậy Ω = {1; 2; 3; 4; 5; 6}.

b) A là biến cố “Số chấm xuất hiện là số lẻ”.

Khi đó, các kết quả thuận lợi cho biến cố A là 1; 3; 5.

⇒ A = {1; 3; 5} ⊂ Ω.

Vậy A = {1; 3; 5}.

c) Biến cố A: “Số chấm xuất hiện là số lẻ” không xảy ra khi số chấm xuất hiện là số chẵn.

⇒ Biến cố đối của A là $\overline{A}$: “Số chấm xuất hiện là số chẵn”.

Các kết quả thuận lợi cho $\overline{A}$ là: 2 ; 4 ; 6.

⇒ $\overline{A}$ = {2 ; 4 ; 6} ⊂ Ω.

Vậy biến cố đối của biến cố A là $\overline{A}$: “Số chấm xuất hiện là số chẵn” và $\overline{A}$ = {2 ; 4 ; 6}.

2. Định nghĩa cổ điển của xác suất

* Định nghĩa cổ điển của xác suất:

Cho phép thử T có không gian mẫu là Ω. Giả thiết rằng các kết quả có thể của T là đồng khả năng. Khi đó nếu E là một biến cố liên quan đến phép thử T thì xác suất của E được cho bởi công thức.

P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}$, trong đó n(Ω) và n(E) tương ứng là số phần tử của tập Ω và tập E.

Nhận xét:

+ Với mỗi biến cố E, ta có 0 ≤ P(E) ≤ 1.

+ Với mỗi biến cố chắc chắn (là tập Ω), ta có P(Ω) = 1.

+ Với mỗi biến cố không thể (là tập ∅), ta có P(∅) = 0.

Ví dụ:Trong phép thử gieo hai con xúc xắc, tính xác suất của các biến cố sau? Hãy nhận xét về hai biến cố đó.

A: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13”;

B: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 13”.

Hướng dẫn giải

Khi gieo mỗi con xúc xắc thì kết quả có thể là xuất hiện mặt 1, 2, …, 6 chấm.

Các kết quả có thể của phép thử là cặp số (i; j), trong đó i, j lần lượt là mặt i chấm, j chấm xuất hiện.

Khi đó, ta có không gian mẫu của phép thử gieo hai con xúc xắc là:

Ω = {(1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6), (2; 1), (2; 2), (2; 3), (2; 4), (2; 5), (2; 6), (3; 1), (3; 2), (3; 3), (3; 4), (3; 5); (3; 6), (4; 1), (4; 2), (4; 3), (4; 4), (4; 5), (4; 6), (5; 1), (5; 2), (5; 3), (5; 4), (5; 5), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6)}.

⇒ n(Ω) = 36.

- Ta thấy tất cả các kết quả có thể trong không gian mẫu đều có tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13.

Do đó, tất cả các kết quả có thể trong không gian mẫu đều thuận lợi cho biến cố A : “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13”.

⇒A = Ω = {(1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6), (2; 1), (2; 2), (2; 3), (2; 4), (2; 5), (2; 6), (3; 1), (3; 2), (3; 3), (3; 4), (3; 5); (3; 6), (4; 1), (4; 2), (4; 3), (4; 4), (4; 5), (4; 6), (5; 1), (5; 2), (5; 3), (5; 4), (5; 5), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6)}.

⇒ n(A) = n(Ω) =36.

⇒P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$= 1.

⇒Biến cố A là biến cố chắc chắn.

- Ta thấy tổng số chấm của hai con xúc xắc luôn nhỏ hơn hoặc bằng 12 nên không có kết quả có thể nào trong không gian mẫu thuận lợi cho biến cố B : “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 13”.

Do đó, có 0 kết quả thuận lợi cho biến cố B.

⇒B = ∅

⇒n(B) = 0 ⇒P(B) =$\frac{n\left(B\right)}{n\left(\Omega \right)}$= 0.

⇒ Biến cố B là biến cố không thể.

Vậy biến cố A: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13” có xác suất bằng 1 và biến cố A là biến cố chắc chắn.

Biến cố B: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 13” có xác suất bằng 0 và biến cố B là biến cố không thể.

Chú ý: Trong những phép thử đơn giản, ta đếm số phần tử của tập Ω và số phần tử của biến cố E bằng cách liệt kê ra tất cả các phần tử của hai tập hợp này.

Ví dụ: Lấy ngẫu nhiên một trong các số nguyên dương lớn hơn 10 và nhỏ hơn 100. Tính xác suất của biến cố B: “Số lấy ra là số chẵn”.

Hướng dẫn giải

Lấy ngẫu nhiên một trong các số nguyên dương lớn hơn 10 và nhỏ hơn 100, tức là lấy ngẫu nhiên một số trong tập hợp {11; 12; 13; …;99}.

⇒ Không gian mẫu của phép thử là Ω = {11; 12; 13; …;99}.

⇒ n(Ω) = 99 – 11 + 1 = 89.

B là biến cố “Số lấy ra là số chẵn”.

Khi đó, các kết quả thuận lợi cho biến cố B là: 12; 14; 16; …; 98.

⇒ B = {12; 14; 16; …; 98}.

⇒ n(B) = $\frac{98-12}{2}+1$ = 44.

⇒ P(B) =$\frac{n\left(B\right)}{n\left(\Omega \right)}$=$\frac{44}{89}$.

Vậy xác suất của biến cố B: “Số lấy ra là số chẵn” là $\frac{44}{89}$.

3. Nguyên lý xác suất bé

- Nếu một biến cố có xác suất rất bé thì trong một phép thử biến cố đó sẽ không xảy ra.

Chú ý: Trong thực tế, xác suất của một biến cố được coi là bé phụ thuộc vào từng trường hợp cụ thể. Chẳng hạn, xác suất của một chiếc điện thoại bị lỗi kĩ thuật là 0,001 được coi là rất bé, nhưng nếu xác suất cháy nổ động cơ của một máy bay là 0,001 thì xác suất này không được coi là bé.

Ví dụ: Xác suất để một bình gas bị chảy nổ là 0,002 thì không thể coi là bé. Nhưng nếu xác suất để tàu về ga chậm là 0,002 thì có thể xem là tàu về ga đúng giờ.

4. Sử dụng phương pháp tổ hợp

Trong nhiều bài toán, để tính số phần tử của không gian mẫu, của các biến cố, ta thường sử dụng các quy tắc đếm, các công thức tính hoán vị, chỉnh hợp và tổ hợp.

Ví dụ:Một hộp có 6 viên bi trắng và 3 viên bi đen. Lấy ngẫu nhiên từ hộp 2 viên bi. Tính xác suất của biến cố E: “Lấy được 1 viên bi trắng”;

Hướng dẫn giải

Trong hộp có 6 viên bi trắng và 3 viên bi đen nên có tổng số bi là 6 + 3 = 9 viên bi.

Lấy ngẫu nhiên 2 viên bi từ hộp, tức là lấy 2 trong 9 viên bi, ta có $C_9^2$= 36 cách.

⇒ n(Ω) = 36.

Biến cố E: “Lấy được 1 viên bi trắng”.

Khi đó:

+ Lấy được 1 viên bi màu trắng trong 6 viên bi trắng, có $C_6^1$cách.

+ Lấy 1 viên bi còn lại không phải màu trắng nên lấy 1 trong 3 viên bi màu đen, ta có: $C_3^1$cách.

Theo quy tắc nhân, ta có $C_6^1$.$C_3^1$= 18 cách lấy 2 viên bi trong đó có 1 viên bi màu trắng.

⇒ n(E) = 18

⇒ P(E) = $\frac{18}{36}$= $\frac{1}{2}$.

Vậy xác suất của biến cố E: “ Lấy được 1 viên bi trắng” là $\frac{1}{2}$.

5. Sử dụng sơ đồ hình cây

Trong một bài toán, phép thử T được hình thành từ một vài phép thử, chẳng hạn: gieo xúc xắc liên tiếp bốn lần; lấy ba viên bi, mỗi viên từ một hộp; …. Khi đó ta sử dụng sơ đồ hình cây để có thể mô tả đầy đủ, trực quan không gian mẫu và biến cố cần tính xác suất.

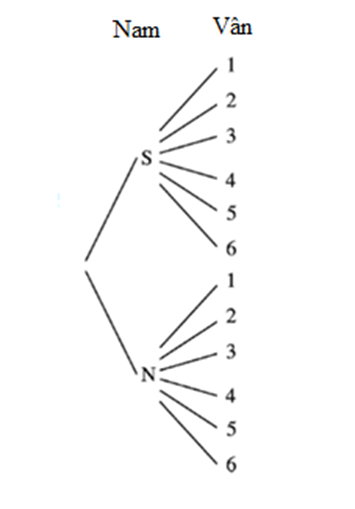
Ví dụ: Hai bạn Nam có một đồng xu, bạn Vân có một con xúc xắc 6 mặt (đồng xu và con xúc xắc đều cân đối, đồng chất). Nam gieo đồng xu, sau đó Vân gieo con xúc xắc.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu của phép thử.

b) Tính xác suất của biến cố A: “Đồng xu xuất hiện mặt sấp” và B: “Con xúc sắc xuất hiện mặt 5 chấm”.

Hướng dẫn giải

a) Nam gieo một đồng xu thì có 2 kết quả có thể là đồng xu xuất hiện mặt sấp (S) hoặc đồng xu xuất hiện mặt ngửa (N).

Vân gieo con xúc xắc thì có 6 kết quả có thể là xuất hiện mặt 1; 2; 3;…; 6 chấm.

Khi đó, ta có sơ đồ hình cây mô tả các kết quả có thể của phép thử như sau:

Từ sơ đồ hình cây ta thấy các kết quả có thể của phép thử là:

(S,1); (S,2); (S,3); (S,4); (S,5); (S,6); (N,1); (N,2); (N,3); (N,4); (N,5); (N,6).

⇒ Không gian mẫu của phép thử là: Ω = {(S,1); (S,2); (S,3); (S,4); (S,5); (S,6); (N,1); (N,2); (N,3); (N,4); (N,5); (N,6)}.

⇒ n(Ω) = 12.

Vậy không gian mẫu của phép thử là: Ω = {(S,1); (S,2); (S,3); (S,4); (S,5); (S,6); (N,1); (N,2); (N,3); (N,4); (N,5); (N,6)}.

b) Với biến cố A: “Đồng xu xuất hiện mặt sấp”

Ta thấy có các kết quả thuận lợi cho A là: (S,1); (S,2); (S,3); (S,4); (S,5); (S,6).

⇒ A = {(S,1); (S,2); (S,3); (S,4); (S,5); (S,6)}.

⇒ n(A) = 6

⇒P(A) =$\frac{n\left(A\right)}{n\left(\Omega \right)}$= $\frac{6}{12}$ = $\frac{1}{2}$.

Với biến cố B: “Con xúc sắc xuất hiện mặt 5 chấm”.

Ta thấy có những kết quả thuận lợi cho biến cố B là: (S,5); (N,5)

⇒ B = {(S,5); (N,5)}

⇒ n(B) = 2

⇒ P(B) =$\frac{n\left(B\right)}{n\left(\Omega \right)}$=$\frac{2}{12}$ = $\frac{1}{6}$.

Vậy xác suất của biến cố A: “Đồng xu xuất hiện mặt sấp” là $\frac{1}{2}$; xác suất của biến cố B: “Con xúc sắc xuất hiện mặt 5 chấm” là $\frac{1}{6}$.

6. Xác suất của biến cố đối

Cho E là một biến cố. Xác suất của biến cố $\overline{E}$ liên hệ với xác suất của biến cố E bởi công thức sau : P(E) = 1 – P($\overline{E}$).

Chú ý: Trong một số bài toán, nếu tính trực tiếp xác suất của biến cố gặp khó khăn, ta có thể tính gián tiếp bằng cách tính xác suất của biến cố đối của nó.

Ví dụ: Trong hộp có một số quả bóng màu đỏ và màu xanh có kích thước và khối lượng như nhau. Nếu lấy ngẫu nhiên hai quả bóng từ hộp thì xác xuất để hai quả này cùng màu là 0,4. Hỏi xác xuất để hai quả bóng lấy ra khác màu là bao nhiêu.

Hướng dẫn giải

Vì biến cố “Lấy được hai quả bóng cùng màu” là biến cố đối của biến cố “Lấy được hai quả bóng khác màu”.

Do đó, xác xuất để hai quả bóng lấy ra khác màu là: 1 - 0, 4 = 0,6.

Vậy xác xuất để hai quả bóng lấy ra khác màu là 0,6.

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Một số nội dung cho hoạt động trải nghiệm hình học

Ước tính số cá thể trong một quần thể

Bài tập cuối năm

Bài 1: Mệnh đề

Bài 2: Tập hợp và các phép toán trên tập hợp - Kết nối tri thức