Giải Toán 10 (Kết nối tri thức): Một số nội dung cho hoạt động trải nghiệm hình học

Giải bài tập Toán 10 Một số nội dung cho hoạt động trải nghiệm hình học 

1. Kiểm tra tính đúng đắn của một kết quả hình học thông qua những ví dụ cụ thể

Chia nhóm lớp (tùy thuộc vào sĩ số mỗi lớp) và chọn một kết quả hình học để kiểm tra, chẳng hạn:

a) Định lí sin đối với một tam giác nội tiếp trong một đường tròn:

Cho tam giác ABC nội tiếp đường tròn. Sử dụng thước đo độ dài để đo độ dài các cạnh và độ dài bán kính của tam giác, thước đo góc để đo các góc của tam giác và máy tính bỏ túi (lấy kết quả gần đúng) để kiểm tra định lí sin: $\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}=2R.$ 

b) Định lí côsin đối với một tam giác:

Cho tam giác ABC. Sử dụng thước đo độ dài để đo độ dài các cạnh của tam giác, thước đo góc để đo các góc của tam giác và máy tính bỏ túi (lấy kết quả gần đúng) để kiểm tra định lí côsin:

BC² = AB² + AC² – 2AB.AC.cosA;

AC² = AB² + BC² – 2AB.BC.cosB;

AB² = AC² + BC² – 2AC.BC.cosC.

c) Đẳng thức $a{h}_a=2\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$ đối với tam giác:

Cho tam giác ABC. Sử dụng thước đo độ dài để đo độ dài các cạnh, độ dài chiều cao h_a (kẻ từ A) của tam giác và máy tính bỏ túi để kiểm tra đẳng thức:

$a{h}_a=2\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}.$

2. Sử dụng kết quả hình học để tính toán trong đo đạc thực tế

Chia nhóm lớp (tùy thuộc vào sĩ số mỗi lớp) và chọn các đối tượng đo đạc khác nhau tương ứng với hai bài toán:

Bài toán 1: Xác định khoảng cách từ vị trí đứng tới một vị trí khác (theo các bước tương ứng được đề cập trong Ví dụ 4, trang 40 của Bài 6, Tập một, SGK).

Bài toán 2: Xác định khoảng cách giữa hai vị trí A, B khác vị trí đứng C.

Đối với bài toán 2, ta cần thực hiện các bước như ở bài toán 1, để xác định khoảng cách từ C tới A và khoảng cách từ C tới B, sau đó, xác định góc C của tam giác ABC.

Khi đó ta tính AB dựa vào định lí côsin đã được học.

3. Gấp giấy, đo đạc và xác định các yếu tố của ba đường conic

Cách xác định các yếu tố của:

a) Một hình elip đã được vẽ trên giấy.

Bước 1: Ta xác định được hai trục đối xứng của elip bằng cách gấp giấy.

Giả sử một trục đối xứng cắt elip tại A₁, A₂ và trục đối xứng còn lại cắt elip tại B₁, B₂ (với A₁A₂ ≥ B₁B₂).

Bước 2: Chọn hệ trục tọa độ Oxy, có O là giao của hai trục đối xứng, tia Ox trùng với tia OA₂, tia Oy trùng với tia OB₂, chọn đơn vị đo trên mặt phẳng tọa độ là cm.

Bước 3: Trong mặt phẳng tọa độ Oxy, elip có phương trình chính tắc là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$ 

Đo độ dài các đoạn A₁A₂, B₁B₂ (đơn vị: cm), ta tính được a, b.

Bước 4: Xác định tiêu cự và vị trí các tiêu điểm.

b) Một hypebol đã được vẽ trên giấy.

Bước 1: Ta xác định được hai trục đối xứng của hypebol bằng cách gấp giấy.

Giả sử một trục đối xứng cắt hypebol tại A₁, A₂.

Bước 2: Chọn hệ trục tọa độ Oxy, có O là giao của hai trục đối xứng, tia Ox trùng với tia OA₂, tia Oy trùng với trục đối xứng còn lại.

Bước 3: Trong mặt phẳng tọa độ Oxy, hypebol có phương trình chính tắc là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Lấy hai điểm trên hypebol, đo trực tiếp (đơn vị: cm) để xác định tọa độ của hai điểm đó, rồi thay vào phương trình trên từ đó tính được a, b.

Bước 4: Xác định tiêu cự và vị trí các tiêu điểm.

c) Một parabol đã được vẽ trên giấy

Bước 1: Ta xác định được hai trục đối xứng và đỉnh của parabol bằng cách gấp giấy.

Bước 2: Chọn hệ trục toạ độ Oxy, có O là giao của hai trục đối xứng cũng đồng thời là đỉnh của parabol, thoả mãn parabol có phương trình chính tắc y² = 2px (đơn vị: cm).

Bước 3: Lấy một điểm trên parabol, đo trực tiếp (đơn vị: cm) để xác định tọa độ của điểm đó, rồi thay vào phương trình parabol để tính p.

Bước 4: Xác định tâm sai, vị trí tiêu điểm và đường chuẩn.

4. Thực hành trải nghiệm trong phòng máy

Thực hiện vẽ hình với phần mềm GeoGebra.

- Vẽ đường tròn (A; R) và điểm B nằm ngoài đường tròn đó. Lấy một điểm C trên đường tròn (A; R) và vẽ M là giao điểm của AC và đường trung trực của đoạn thẳng BC. Cho điểm C thay đổi và dùng lệnh tìm quỹ tích để thấy rằng M thay đổi trên một nhánh hypebol.

Các bước thực hiện như sau:

Bước 1: Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.

Bước 2: Vẽ đường tròn (A; R):

Chẳng hạn, lấy R = 5, ta vẽ đường tròn (A; 5) như sau: Trên thanh công cụ chọn   → Chọn  → Nhấn chuột trái vào một điểm bất kì trên vùng làm việc để có tâm A → Nhập số 5 ứng với bán kính của đường tròn như hình vẽ dưới đây:

 

Nhấn “OK”, ta được đường tròn như hình vẽ:

 

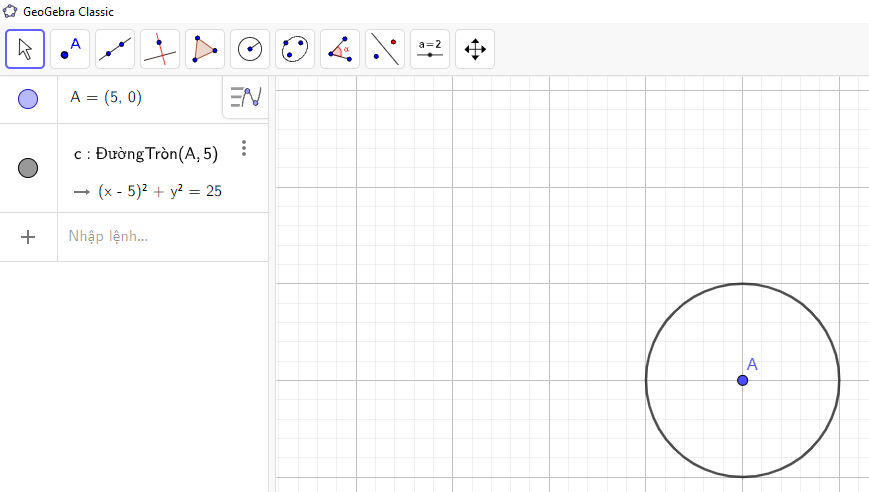
Bước 3: Lấy 1 điểm B bất kì nằm ngoài đường tròn.

Trên thanh công cụ ta chọn  → Chọn   → Nhấn chuột trái vào một điểm nằm ngoài đường tròn như hình vẽ:

 

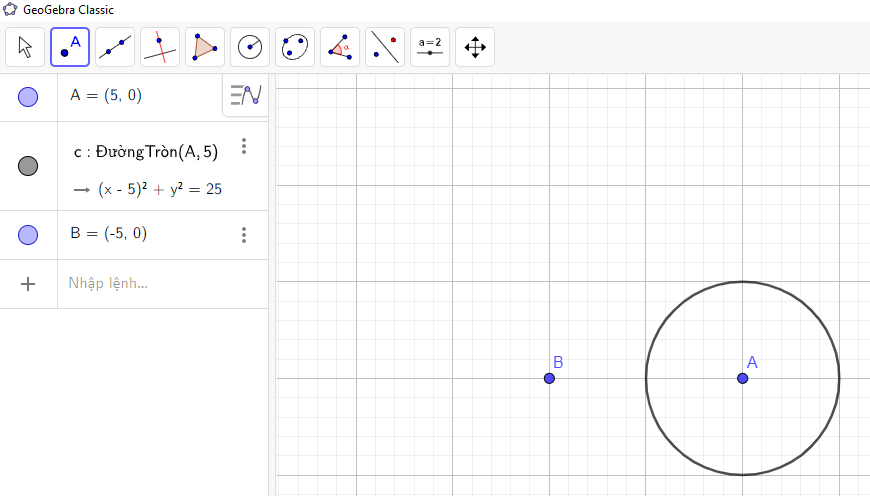
Bước 4: Lấy một điểm C trên đường tròn:

Ta nhấn chuột trái vào một điểm trên đường tròn đã vẽ, ta được điểm C như hình vẽ:

 

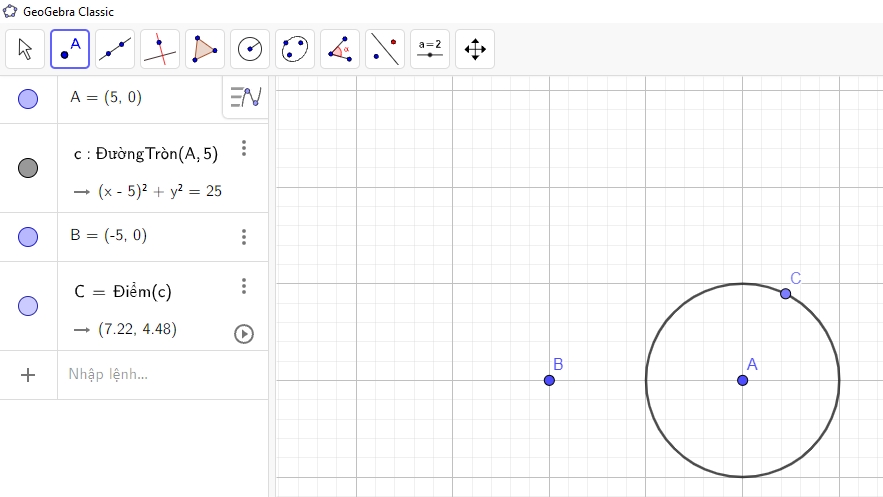
Bước 5: Vẽ đường thẳng AC

Trên thanh công cụ, ta chọn  → Chọn  → Nhấn chuột trái vào hai điểm A và C ta được hình vẽ:

 

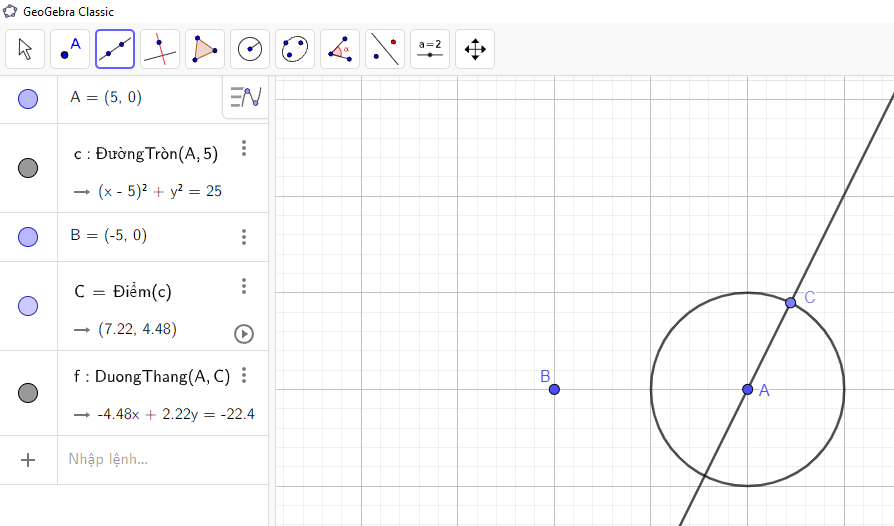
Bước 6: Vẽ đoạn thẳng BC:

Trên thanh công cụ, ta chọn  → Chọn  → Nhấn chuột trái vào điểm B và điểm C ta được hình vẽ:

 

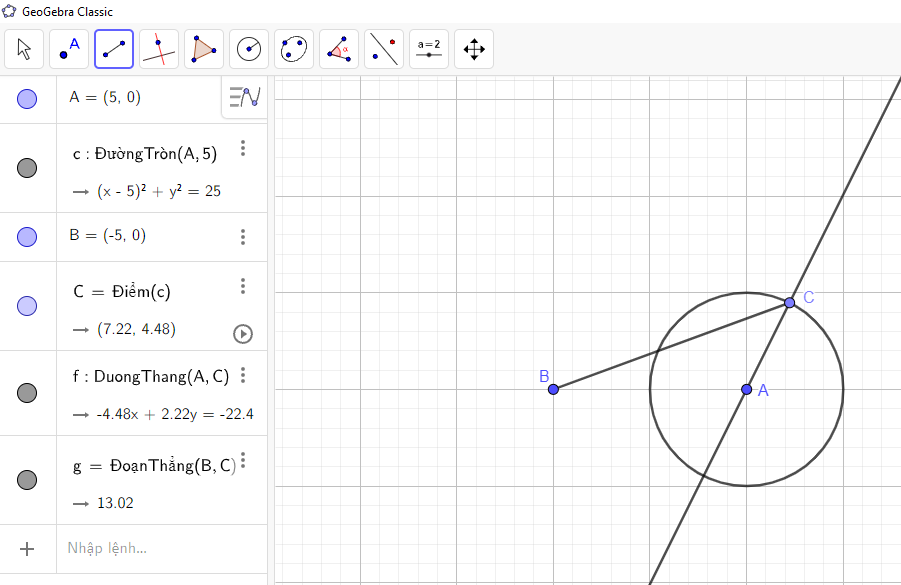
Bước 7: Vẽ đường trung trực của đoạn thẳng BC:

Trên thanh công cụ, chọn  → Chọn → Nhấn chuột trái vào hai điểm B và C ta được như hình vẽ:

 

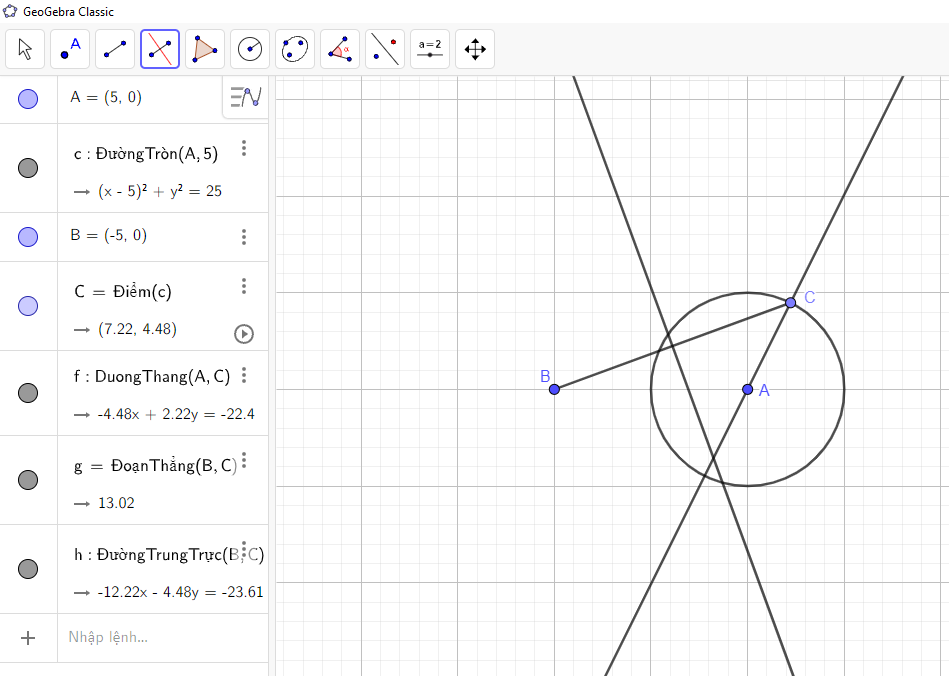
Bước 8: Lấy giao điểm của AC và trung trực của đoạn thẳng BC:

Trên thanh công cụ, ta chọn  → Chọn → Nhấn chuột trái vào đường thẳng AC và trung trực đoạn thẳng BC ta được như hình vẽ:

 

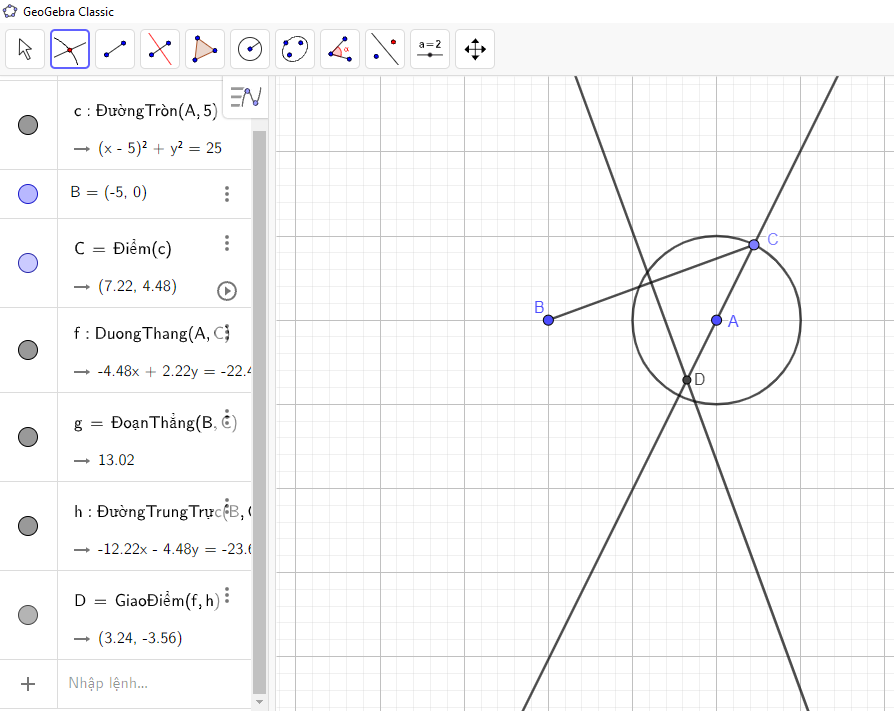
Bước 9: Đổi tên giao điểm D thành giao điểm M:

Trên thanh công cụ, chọn  → Nhấn chuột trái vào điểm D → Nhấn chuột phải → Chọn để đổi D thành M.

 

Nhấn “OK”, ta được như hình vẽ:

 

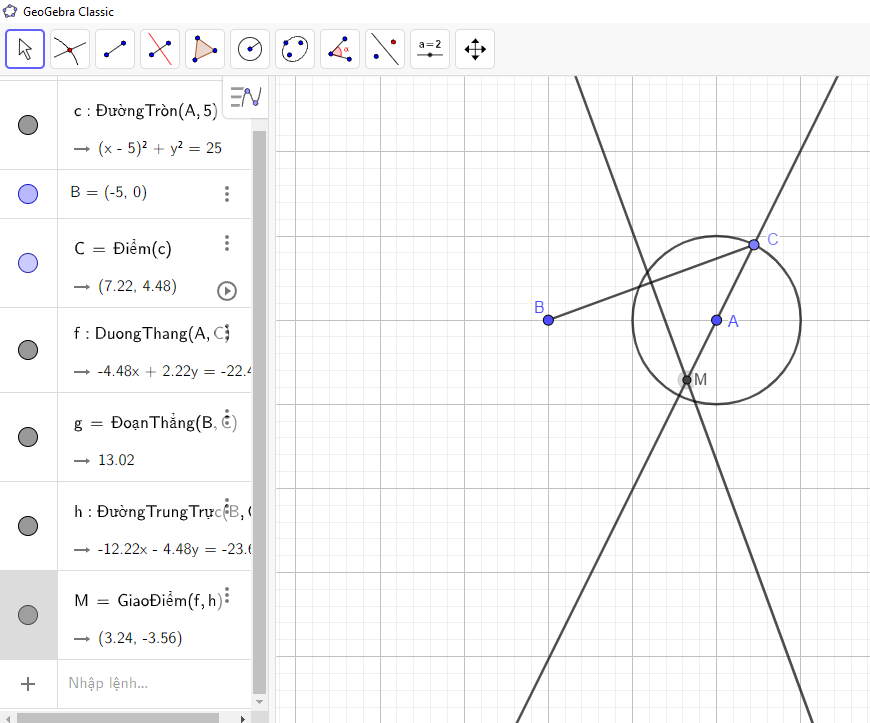
Bước 10: Cho điểm M hiện thị dấu vết khi di chuyển:

Nhấn chuột trái chọn điểm M → Nhấn chuột phải → Chọn

Bước 11: Cho điểm C di chuyển trên đường tròn (A; R):

Nhấn chuột trái chọn điểm C → Nhấn chuột phải → Chọn

Khi đó điểm C di chuyển dẫn đến M di chuyển trên một hypebol như hình vẽ

 

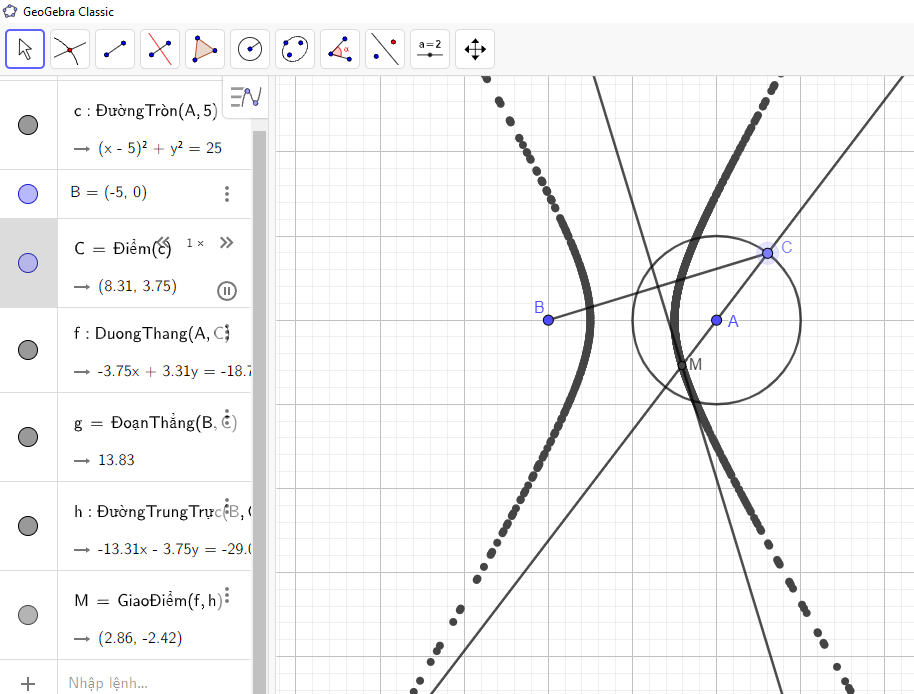
- Tương tự ta thực hiện các hình vẽ sau:

- Vẽ đường tròn (A; R) và điểm B nằm trong đường tròn đó. Lấy một điểm C trên đường tròn (A; R) và vẽ M là giao điểm của AC và đường tròn trung trực của đoạn thẳng BC. Cho điểm C thay đổi và dùng lệnh tìm quỹ tích để thấy M thay đổi trên một elip.

Vẽ tương tự như hoạt động trên, chỉ khác tại Bước 3, điểm B thay vì nằm ngoài đường tròn thì ta lấy bên trong đường tròn.

Khi đó, điểm C di chuyển thì ta được M chạy trên một elip như hình vẽ:

 

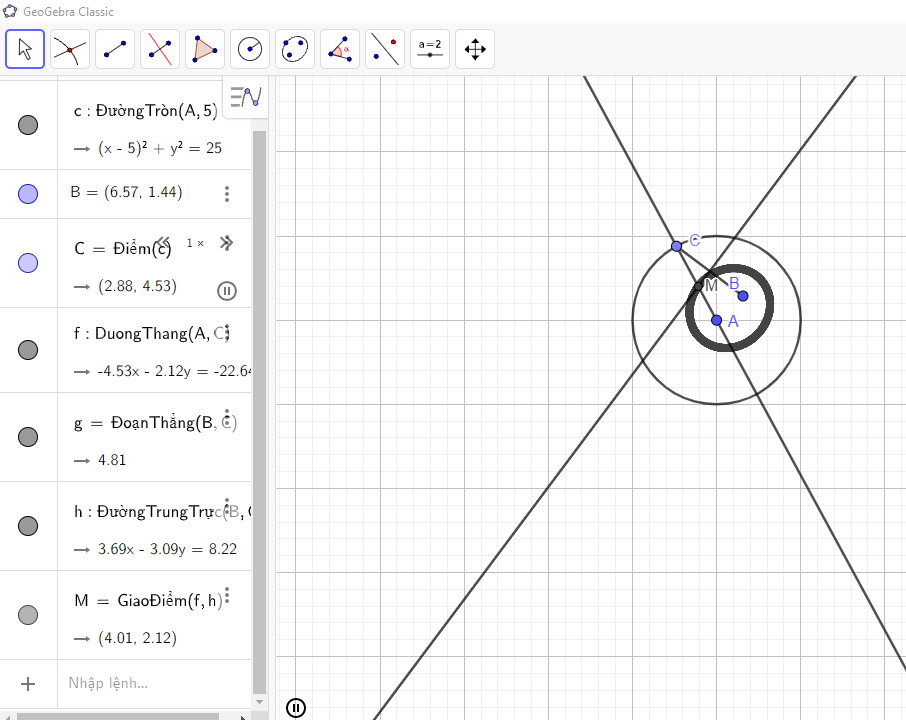
- Vẽ một số đường tròn (ω₁), (ω₂), (ω₃), … có cùng tâm O₁ tương ứng có bánh kính R₁, R₁ + a, R₁ + 2a, … và một số đường tròn (Ω₁), (Ω₂), (Ω₃), … có cùng tâm O₂, tương ứng có bán kính R₂, R₂ + a, R₂ + 2a, … (R₁ ≠ R₂). Khi đó, em sẽ quan sát thấy các cặp giao điểm A₁, B₁; A₂, B₂; A₃, B₃; … tương ứng của (ω₁) và (Ω₁); (ω₂) và (Ω₂); (ω₃) và (Ω₃); … là cùng thuộc một nhánh của một hypebol. Kết quả này tương ứng với một hiện tượng vật lí mà em có thể quan sát được: Ném hai hòn sỏi (bằng nhau) xuống mặt hồ lặng sóng, thì em sẽ thấy hai họ đường tròn sóng nước và nói chung giao của chúng tạo nên một đường hypebol.

Chẳng hạn, ta lấy R₁ = 3, R₂ = 5 và a = 1, ta vẽ được các đường tròn trên như sau:

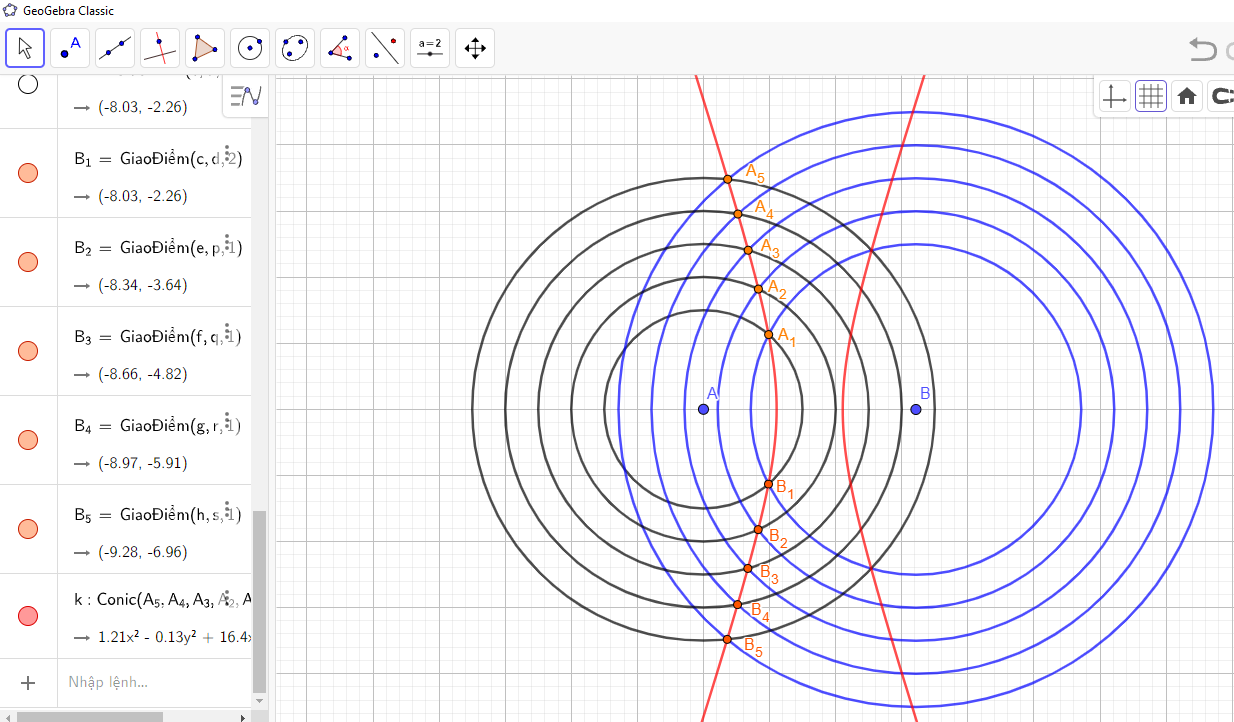
Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Ước tính số cá thể trong một quần thể

Bài tập cuối năm

Bài 1: Mệnh đề

Bài 2: Tập hợp và các phép toán trên tập hợp - Kết nối tri thức

Bài tập cuối chương 1