12 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Tổng hợp)

Câu 1:

17/07/2024

Cho tam giác ABC có cạnh BC = 6 và đường cao AH (H ∈ BC) sao cho BH = 2HC. Tính $\vec{A B} . \vec{B C}$

A. -24

B. 24

C. 18

D. -18

Xem đáp án

Đáp án A

Ta có:

$\vec{A B} . \vec{B C} = (\vec{A H} + \vec{H B}) . \vec{B C} = \vec{A H} . \vec{B C} + \vec{H B} . \vec{B C} = \vec{H B} . \vec{B C} = H B . B C . \cos (\vec{H B}, \vec{B C}) = \frac{2}{3} B C . B C . \cos (\vec{H B} . \vec{B C}) = \frac{2}{3} .6.6. \cos 180^{0} = - 24$

Câu 2:

17/07/2024

Cho tam giác đều ABC có cạnh bằng a và chiều cao AH. Mệnh đề nào sau đây là sai?

A. $\vec{A H} . \vec{B C} = 0$

B. $(\vec{A B}, \vec{H A}) = 150^{0}$

C. $\vec{A B} . \vec{A C} = \frac{a^{2}}{2}$

D. $\vec{A C} . \vec{C B} = \frac{a^{2}}{2}$

Xem đáp án

Đáp án D

Đáp án A: đúng do $A H ⊥ B C$

Đáp án B: đúng do $(\vec{A B}, \vec{A H}) = 30^{\circ}$ nên $(\vec{A B}, \vec{H A}) = 150^{\circ}$

Đáp án C: đúng do

$\vec{A B} . \vec{A C} = A B . A C . \cos (\vec{A B} . \vec{A C}) = a . a . \cos 60^{0} = \frac{a^{2}}{2}$

Đáp án D: do $(\vec{A C} . \vec{C B})$ là góc ngoài của góc $\hat{C}$ nên $(\vec{A C} . \vec{C B}) = 120^{\circ}$

Do đó

$\vec{A C} . \vec{C B} = A C . C B . \cos (\vec{A C}, \vec{C B}) = a . a . \cos 120^{0} = - \frac{a^{2}}{2}$

Câu 3:

17/07/2024

Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai?

A. $(\vec{A B} . \vec{A C}) \vec{B C} = 2 \vec{B C}$

B. $\vec{B C} . \vec{C A} = - 2$

C. $(\vec{A B} + \vec{B C}) . \vec{A C} = - 4$

D. $(\vec{B C} - \vec{A C}) . \vec{B A} = 4$

Xem đáp án

Đáp án C

Ta đi tính tích vô hướng ở các phương án. So sánh vế trái với vế phải

Phương án A: $\vec{A B} . \vec{A C} = A B . A C . \cos 60^{0} = 2$

$\Rightarrow (\vec{A B} . \vec{A C}) \vec{B C} = 2 \vec{B C}$ nên loại A

Phương án B: $\vec{B C} . \vec{C A} = B C . A C . \cos 120^{0} = - 2$ nên loại B

Phương án C: $(\vec{A B} + \vec{B C}) . \vec{A C} = \vec{A C} . \vec{A C} = 4$ nên chọn C

Phương án D:

$(\vec{B C} - \vec{A C}) . \vec{B A} = (- \vec{C B} + \vec{C A}) . \vec{B A} = (\vec{C A} - \vec{C B}) . \vec{B A} = \vec{B A} . \vec{B A} = B A^{2} = 4$

nên loại D

Câu 4:

08/11/2024

Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?

A. $\vec{A B} . \vec{A C} = \frac{1}{2} a^{2}$

B. $\vec{A C} . \vec{C B} = - \frac{1}{2} a^{2}$

C. $\vec{G A} . \vec{G B} = \frac{a^{2}}{6}$

D. $\vec{A B} . \vec{A G} = \frac{1}{2} a^{2}$

Xem đáp án

Đáp án đúng: C

*Lời giải:

Dựa vào đáp án. Ta có nhận xét sau:

Xác định được góc $(\vec{A B}, \vec{A C})$ là $\hat{A}$ nên $(\vec{A B}, \vec{A C}) = 60^{0}$

Do đó,

$\vec{A B} . \vec{A C} = A B . A C . \cos (\vec{A B}, \vec{A C}) = a . a . \cos 60^{0} = \frac{1}{2} a^{2}$

nên A đúng

Xác định được góc $(\vec{A C}, \vec{C B})$ là góc ngoài của $\hat{C}$ nên $(\vec{A C}, \vec{C B}) = 120^{0}$

Do đó,

$\vec{A C} . \vec{C B} = A C . C B . \cos (\vec{A C}, \vec{C B}) = a . a . \cos 120^{0} = - \frac{1}{2} a^{2}$

nên B đúng

Xác định được góc $(\vec{G A} . \vec{G B})$ là $\hat{A G B}$ nên $(\vec{G A} . \vec{G B}) = 120^{0}$

Do đó,

$\vec{G A} . \vec{G B} = G A . G B . \cos (\vec{G A} . \vec{G B}) = \frac{a}{\sqrt{3}} . \frac{a}{\sqrt{3}} . \cos 120^{0} = - \frac{a^{2}}{6}$

nên C sai

Xác định được góc $(\vec{A B}, \vec{A G})$ là $\hat{G A B}$ nên $(\vec{A B}, \vec{A G}) = 30^{0}$

Do đó,

$\vec{A B} . \vec{A G} = A B . A G . \cos (\vec{A B}, \vec{A G}) = a . \frac{a}{\sqrt{3}} . \cos 30^{0} = \frac{a^{2}}{2}$

nên D đúng

*Phương pháp giải:

- áp dụng tính chất về tích vô hướng của hai vectơ:

- Định nghĩa tích vô hướng: Cho hai vectơ $\vec{a}$ và $\vec{b}$ ( $\vec{a}, \vec{b} \neq \vec{0}$ ), khi đó tích vô hướng của $\vec{a}$ và $\vec{b}$ kí hiệu là $\vec{a} . \vec{b}$ và xác định bởi công thức: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ .

* Lý thuyết nắm thêm và các công thức về tích vô hướng của hai vectơ:

- Định nghĩa góc giữa hai vectơ: Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $\vec{0}$ . Từ điểm O bất kì vẽ $\vec{O A} = \vec{a}$ , $\vec{O B} = \vec{b}$ , khi đó góc $\hat{A O B}$ ( $0^{o} \leq \hat{A O B} \leq 180^{o}$ ) là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ . Kí hiệu: $(\vec{a}, \vec{b})$ .

- Định nghĩa tích vô hướng: Cho hai vectơ $\vec{a}$ và $\vec{b}$ ( $\vec{a}, \vec{b} \neq \vec{0}$ ), khi đó tích vô hướng của $\vec{a}$ và $\vec{b}$ kí hiệu là $\vec{a} . \vec{b}$ và xác định bởi công thức: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ .

- Chú ý:

+) Khi ít nhất một trong hai vectơ $\vec{a}$ và $\vec{b}$ bằng vectơ $\vec{0}$ ta quy ước: $\vec{a} . \vec{b} = 0$ .

+) Với hai vectơ $\vec{a}$ và $\vec{b}$ (), ta có: $\vec{a} . \vec{b} = 0 \Leftrightarrow \vec{a} ⊥ \vec{b}$ .

+) Tích vô hướng $\vec{a} . \vec{a}$ được kí hiệu là ${\vec{a}}^{2}$ và ta có: ${\vec{a}}^{2} = {|\vec{a}|}^{2}$ .

- Các tính chất của tích vô hướng:

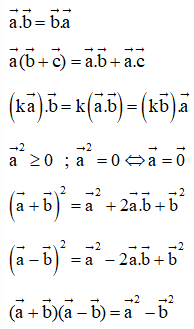
- Biểu thức tọa độ của tích vô hướng: Trong mặt phẳng $(O; \vec{i}, \vec{j})$ , cho hai vectơ $\vec{a} = (a_{1}; a_{2})$ và $\vec{b} = (b_{1}; b_{2})$ . Khi đó: $\vec{a} . \vec{b} = a_{1} b_{1} + a_{2} b_{2}$ . Và với hai vectơ $\vec{a} = (a_{1}; a_{2})$ và $\vec{b} = (b_{1}; b_{2})$ đều khác $\vec{0}$ thì $\vec{a} ⊥ \vec{b} \Leftrightarrow a_{1} b_{1} + a_{2} b_{2} = 0$ .

- Ứng dụng của tích vô hướng:

+) Độ dài của vectơ $\vec{a} = (a_{1}; a_{2})$ được tính theo công thức: $|\vec{a}| = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}}$

+) Góc giữa hai vectơ $\vec{a} = (a_{1}; a_{2})$ và $\vec{b} = (b_{1}; b_{2})$ ( $\vec{a}; \vec{b} \neq \vec{0}$ ):

$\cos (\vec{a}; \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{a_{1}^{2} + a_{2}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2}}}$

+) Khoảng cách giữa hai điểm $A (x_{A}; y_{A})$ và $B (x_{B}; y_{B})$ được tính theo công thức:

$A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$

Các dạng bài.

Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.

- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức $\vec{a} . \vec{b} = a_{1} b_{1} + a_{2} b_{2}$

- Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức: $\cos (\vec{a}; \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{a_{1}^{2} + a_{2}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2}}}$

Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ.

Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức $A B^{2} = {|\vec{A B}|}^{2} = {\vec{A B}}^{2}$ . Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức: $|\vec{A B}| = A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$ .

Xem thêm các bài viết liên quan hay, chi tiết:

Tích vô hướng của hai vectơ và cách giải bài tập (2024) chi tiết nhất

Giải Toán 10 Bài 4 (Chân trời sáng tạo): Tích vô hướng của hai vectơ

Trắc nghiệm Tích vô hướng của hai vecto có đáp án – Toán lớp 10

Câu 5:

23/07/2024

Cho hình vuông ABCD cạnh a. Tính $P = (\vec{A B} + \vec{A C}) . (\vec{B C} + \vec{B D} + \vec{B A})$

A. $P = 2 \sqrt{2} a$

B. $P = 2 a^{2}$

C. $P = a^{2}$

D. $P = - 2 a^{2}$

Xem đáp án

Đáp án D

Ta có:

$\vec{B C} + \vec{B D} + \vec{B A} = (\vec{B C} + \vec{B A}) + \vec{B D} = \vec{B D} + \vec{B D} = 2 \vec{B D}$

và $B D = a \sqrt{2}$

Khi đó

$P = (\vec{A B} + \vec{A C}) .2 \vec{B D} = 2 \vec{A B} . \vec{B D} + 2 \vec{A C} . \vec{B D} = - 2 \vec{B A} . \vec{B D} + 0 = - 2. B A . B D \cos (\vec{B A} . \vec{B D}) = 2. a . a \sqrt{2} . \frac{\sqrt{2}}{2} = - 2 a^{2}$

Câu 6:

23/07/2024

Cho hình thoi ABCD có AC = 8 và BD = 6. Tính $\vec{A B} . \vec{A C}$

A. $\vec{A B} . \vec{A C} = 24$

B. $\vec{A B} . \vec{A C} = 26$

C. $\vec{A B} . \vec{A C} = 28$

D. $\vec{A B} . \vec{A C} = 32$

Xem đáp án

Đáp án D

Gọi $O = A C \cap B D$ , giả thiết không cho góc, ta phân tích các vec tơ $\vec{A B}, \vec{A C}$ theo các vec tơ có giá vuông góc với nhau. Ta có:

$\vec{A B} . \vec{A C} = (\vec{A O} + \vec{O B}) . \vec{A C} = \vec{A O} . \vec{A C} + \vec{O B} . \vec{A C} = \frac{1}{2} \vec{A C} . \vec{A C} + 0 = \frac{1}{2} A C^{2} = 32$

Câu 7:

20/07/2024

Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Khi đó $(\vec{I A} + \vec{I B}) . \vec{I D}$ bằng:

A. $\frac{9 a^{2}}{2}$

B. $- \frac{9 a^{2}}{2}$

C. 0

D. $9 a^{2}$

Xem đáp án

Đáp án B

Ta có:

$(\vec{I A} + \vec{I B}) . \vec{I D} = (\vec{I A} + \vec{I A} + \vec{A B}) . \vec{I D} = 2 \vec{I A} . \vec{I D} = 2. I A . I D . c o s 180 ° = - 2. \frac{3 a}{2} . \frac{3 a}{2} .1 = - \frac{9 a^{2}}{2}$

(do $A B ⊥ I D$ nên $\vec{A B} . \vec{I D} = 0$ )

Câu 8:

17/07/2024

Cho tam giác đều ABC cạnh a, với các đường cao AH, BK; vẽ $H I ⊥ A C$ . Câu nào sau đây đúng?

A. $\vec{B A} . \vec{B C} = 2 \vec{B A} . \vec{B H}$

B. $\vec{C B} . \vec{C A} = 4 \vec{C B} . \vec{C I}$

C. $(\vec{A C} - \vec{A B}) . \vec{B C} = 2 \vec{B A} . \vec{B C}$

D. Cả 3 câu trên

Xem đáp án

Đáp án D

Phương án A: $\vec{B C} = 2 \vec{B H} \Rightarrow \vec{B A} . \vec{B C} = 2 \vec{B A} . \vec{B H}$ nên đẳng thức ở phương án A là đúng

Phương án B: $\vec{C A} = 4 \vec{C I} \Rightarrow \vec{C B} . \vec{C A} = 4 \vec{C B} . \vec{C I}$ nên đẳng thức ở phương án B là đúng

Phương án C:

$\begin{matrix} (\vec{A C} - \vec{A B}) . \vec{B C} = \vec{B C} . \vec{B C} = a^{2} \\ 2 \vec{B A} . \vec{B C} = 2. a . a . \frac{1}{2} = a^{2} \end{matrix}\} \Rightarrow (\vec{A C} - \vec{A B}) . \vec{B C} = 2 \vec{B A} . \vec{B C}$

Nên đẳng thức ở phương án C là đúng

Vậy chọn D

Câu 9:

19/07/2024

Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2) và B (−3; 1). Tìm tọa độ điểm C thuộc trục tung sao cho tam giác ABC vuông tại A

A. C (0; 6)

B. C (5; 0)

C. C (3; 1)

D. C (0; −6)

Xem đáp án

Đáp án A

Ta có $C \in O y$ nên C (0; c) và $\{\begin{matrix} \vec{A B} = (- 4; - 1) \\ \vec{A C} = (- 1; c - 2) \end{matrix}$

Vì tam giác ABC vuông tại A nên suy ra $\vec{A B} . \vec{A C} = 0$ nên $(- 4) . (- 1) + (- 1) (c - 2) = 0$

$\Leftrightarrow c = 6$

Vậy C (0; 6)

Câu 10:

17/07/2024

Cho hai điểm A (−3, 2), B (4, 3). Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M

A. M (7; 0)

B. M (5; 0)

C. M (3; 0)

D. M (9; 0)

Xem đáp án

Đáp án C

Ta có A (−3, 2), B (4, 3). Gọi M (x; 0), x > 0

Khi đó $\vec{A M} = (x + 3; - 2), \vec{B M} = (x - 4; - 3)$

Theo YCBT

$\Leftrightarrow \vec{A M} . \vec{B M} = 0 \Leftrightarrow x^{2} - x - 6 = 0 \Rightarrow [\begin{matrix} x = - 2 (l) \\ x = 3 \end{matrix} \Rightarrow M (3; 0)$

Câu 11:

17/07/2024

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A (−1; 1), B (1; 3) và C (1; −1). Khẳng định nào sau đây là đúng?

A. Tam giác ABC đều

B. Tam giác ABC có ba góc đều nhọn

C. Tam giác ABC cân tại B

D. Tam giác ABC vuông cân tại A

Xem đáp án

Đáp án D

Ta có: $\vec{A B} = (2; 2), \vec{B C} = (0; - 4)$ và $\vec{A C} = (2; - 2)$

Suy ra $\{\begin{matrix} A B = A C = 2 \sqrt{2} \\ A B^{2} + A C^{2} = B C^{2} \end{matrix}$

Vậy tam giác ABC vuông cân tại A

Câu 12:

14/07/2024

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A (10; 5), B(3;2) và C(6; −5). Khẳng định nào sau đây là đúng?

A. Tam giác ABC đều

B. Tam giác ABC vuông cân tại A

C. Tam giác ABC vuông cân tại B

D. Tam giác ABC có góc A tù

Xem đáp án

Đáp án C

Ta có: $\vec{A B} = (- 7; - 3), \vec{B C} = (3; - 7)$ và $\vec{A C} = (- 4; - 10)$

Suy ra $\vec{A B} . \vec{B C} = (- 7) .3 + (- 3) . (- 7) = 0$ và AB = BC

Vậy tam giác ABC vuông cân tại B

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3