Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?

Đáp án đúng: C

*Lời giải:

Dựa vào đáp án. Ta có nhận xét sau:

• Xác định được góc $\left(\overrightarrow{AB},\overrightarrow{AC}\right)$ là $\widehat{A}$ nên $\left(\overrightarrow{AB},\overrightarrow{AC}\right)={60}^0$

Do đó, 

$$\begin{gathered} \overrightarrow{AB}.\overrightarrow{AC}=AB.AC.\cos \left(\overrightarrow{AB},\overrightarrow{AC}\right) \\ =a.a.\cos {60}^0=\frac{1}{2}{a}^2 \end{gathered}$$

nên A đúng

• Xác định được góc $\left(\overrightarrow{AC},\overrightarrow{CB}\right)$ là góc ngoài của $\widehat{C}$ nên $\left(\overrightarrow{AC},\overrightarrow{CB}\right)={120}^0$

Do đó,

$$\begin{gathered} \overrightarrow{AC}.\overrightarrow{CB}=AC.CB.\cos \left(\overrightarrow{AC},\overrightarrow{CB}\right) \\ =a.a.\cos {120}^0=-\frac{1}{2}{a}^2 \end{gathered}$$

nên B đúng

• Xác định được góc $\left(\overrightarrow{GA}.\overrightarrow{GB}\right)$ là $\widehat{AGB}$ nên $\left(\overrightarrow{GA}.\overrightarrow{GB}\right)={120}^0$

Do đó,

$$\begin{gathered} \overrightarrow{GA}.\overrightarrow{GB}=GA.GB.\cos \left(\overrightarrow{GA}.\overrightarrow{GB}\right) \\ =\frac{a}{\sqrt{3}}.\frac{a}{\sqrt{3}}.\cos {120}^0=-\frac{a^2}{6} \end{gathered}$$

nên C sai

• Xác định được góc $\left(\overrightarrow{AB},\overrightarrow{AG}\right)$ là $\widehat{GAB}$ nên $\left(\overrightarrow{AB},\overrightarrow{AG}\right)={30}^0$

Do đó,

$$\begin{gathered} \overrightarrow{AB}.\overrightarrow{AG}=AB.AG.\cos \left(\overrightarrow{AB},\overrightarrow{AG}\right) \\ =a.\frac{a}{\sqrt{3}}.\cos {30}^0=\frac{a^2}{2} \end{gathered}$$

nên D đúng

*Phương pháp giải:

- áp dụng tính chất về tích vô hướng của hai vectơ: 

- Định nghĩa tích vô hướng: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ($\overrightarrow{a},\overrightarrow{b}\ne \overrightarrow{0}$), khi đó tích vô hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$ kí hiệu là $\overrightarrow{a}.\overrightarrow{b}$ và xác định bởi công thức: $\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos \left(\overrightarrow{a},\overrightarrow{b}\right)$.

* Lý thuyết nắm thêm và các công thức về tích vô hướng của hai vectơ:

- Định nghĩa góc giữa hai vectơ: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$. Từ điểm O bất kì vẽ $\overrightarrow{OA}=\overrightarrow{a}$, $\overrightarrow{OB}=\overrightarrow{b}$, khi đó góc $\widehat{AOB}$ ($0^o\le \widehat{AOB}\le {180}^o$) là góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$. Kí hiệu: $\left(\overrightarrow{a},\overrightarrow{b}\right)$.

- Định nghĩa tích vô hướng: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ($\overrightarrow{a},\overrightarrow{b}\ne \overrightarrow{0}$), khi đó tích vô hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$ kí hiệu là $\overrightarrow{a}.\overrightarrow{b}$ và xác định bởi công thức: $\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos \left(\overrightarrow{a},\overrightarrow{b}\right)$.

- Chú ý:

+) Khi ít nhất một trong hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng vectơ $\overrightarrow{0}$ ta quy ước: $\overrightarrow{a}.\overrightarrow{b}=0$.

+) Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ (), ta có: $\overrightarrow{a}.\overrightarrow{b}=0\iff \overrightarrow{a}\perp \overrightarrow{b}$.

+) Tích vô hướng $\overrightarrow{a}.\overrightarrow{a}$ được kí hiệu là ${\overrightarrow{a}}^2$ và ta có: ${\overrightarrow{a}}^2={\left|\overrightarrow{a}\right|}^2$.

- Các tính chất của tích vô hướng:

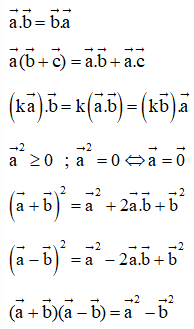
- Biểu thức tọa độ của tích vô hướng: Trong mặt phẳng $\left(O;\overrightarrow{i},\overrightarrow{j}\right)$, cho hai vectơ $\overrightarrow{a}=\left(a_1;a_2\right)$ và $\overrightarrow{b}=\left(b_1;b_2\right)$. Khi đó: $\overrightarrow{a}.\overrightarrow{b}=a_1{b}_1+a_2{b}_2$. Và với hai vectơ $\overrightarrow{a}=\left(a_1;a_2\right)$ và $\overrightarrow{b}=\left(b_1;b_2\right)$ đều khác $\overrightarrow{0}$ thì $\overrightarrow{a}\perp \overrightarrow{b}\iff a_1{b}_1+a_2{b}_2=0$.

- Ứng dụng của tích vô hướng:

+) Độ dài của vectơ $\overrightarrow{a}=\left(a_1;a_2\right)$ được tính theo công thức: $\left|\overrightarrow{a}\right|=\sqrt{{a_1}^2+{a_2}^2}$

+) Góc giữa hai vectơ $\overrightarrow{a}=\left(a_1;a_2\right)$ và $\overrightarrow{b}=\left(b_1;b_2\right)$ ( $\overrightarrow{a};\overrightarrow{b}\ne \overrightarrow{0}$):

$\cos \left(\overrightarrow{a};\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$

+) Khoảng cách giữa hai điểm $A\left(x_A;y_A\right)$ và $B\left(x_B;y_B\right)$ được tính theo công thức:

$AB=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$

Các dạng bài.

Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.

- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức $\overrightarrow{a}.\overrightarrow{b}=a_1{b}_1+a_2{b}_2$

- Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức: $\cos \left(\overrightarrow{a};\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$

Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ.

Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức $A{B}^2={\left|\overrightarrow{AB}\right|}^2={\overrightarrow{AB}}^2$. Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức: $\left|\overrightarrow{AB}\right|=AB=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$.

Xem thêm các bài viết liên quan hay, chi tiết:

Tích vô hướng của hai vectơ và cách giải bài tập (2024) chi tiết nhất 

Giải Toán 10 Bài 4 (Chân trời sáng tạo): Tích vô hướng của hai vectơ 

Trắc nghiệm Tích vô hướng của hai vecto có đáp án – Toán lớp 10