Câu hỏi:
17/07/2024 385
Điểm nào là tiêu điểm của parabol y2 = 5x?
Điểm nào là tiêu điểm của parabol y2 = 5x?
A. F(5; 0);
A. F(5; 0);
B. \(F\left( {\frac{5}{2};0} \right)\);
B. \(F\left( {\frac{5}{2};0} \right)\);
C. \(F\left( { \pm \frac{5}{4};0} \right)\);
C. \(F\left( { \pm \frac{5}{4};0} \right)\);
D. \(F\left( {\frac{5}{4};0} \right)\).
D. \(F\left( {\frac{5}{4};0} \right)\).
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Phương trình chính tắc của parabol (P) có dạng: y = 2px (p > 0).
Ta có 2p = 5. Suy ra \(p = \frac{5}{2}\).
Khi đó \(\frac{p}{2} = \frac{5}{4}\).
Vậy tiêu điểm của parabol (P) là \(F\left( {\frac{5}{4};0} \right)\).
Do đó ta chọn phương án D.
Đáp án đúng là: D
Phương trình chính tắc của parabol (P) có dạng: y = 2px (p > 0).
Ta có 2p = 5. Suy ra \(p = \frac{5}{2}\).
Khi đó \(\frac{p}{2} = \frac{5}{4}\).
Vậy tiêu điểm của parabol (P) là \(F\left( {\frac{5}{4};0} \right)\).
Do đó ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm (cho giống lúa mới) có cùng diện tích được trình bày trong bảng phân bố tần số sau đây:
Sản lượng
20
21
22
23
24
Tần số
5
8
11
10
6
Hỏi sản lượng lúa trung bình thu được là bao nhiêu tạ? Tìm khoảng tứ phân vị của dãy số liệu trên.
Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm (cho giống lúa mới) có cùng diện tích được trình bày trong bảng phân bố tần số sau đây:
|
Sản lượng |
20 |
21 |
22 |
23 |
24 |
|
Tần số |
5 |
8 |
11 |
10 |
6 |
Hỏi sản lượng lúa trung bình thu được là bao nhiêu tạ? Tìm khoảng tứ phân vị của dãy số liệu trên.
Câu 2:
Đường tròn tâm I(1; 4) và đi qua điểm B(2; 6) có phương trình là:
Đường tròn tâm I(1; 4) và đi qua điểm B(2; 6) có phương trình là:
Câu 3:
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Viết phương trình đường thẳng (d) qua A(3; 2) và tiếp xúc với (C).
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Viết phương trình đường thẳng (d) qua A(3; 2) và tiếp xúc với (C).
Câu 4:
Điểm thi học kì I môn Toán của lớp 10A được thống kê trong bảng sau:
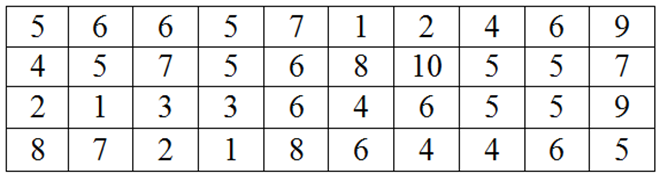
Điểm trung bình môn Toán của lớp 10A2 là
Điểm thi học kì I môn Toán của lớp 10A được thống kê trong bảng sau:
Điểm trung bình môn Toán của lớp 10A2 là
Câu 5:
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Tìm điểm M thuộc (d’): x – 2y – 1 = 0 sao cho từ M vẽ được hai tiếp tuyến đến (C) vuông góc với nhau.
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Tìm điểm M thuộc (d’): x – 2y – 1 = 0 sao cho từ M vẽ được hai tiếp tuyến đến (C) vuông góc với nhau.
Câu 6:
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Viết phương trình đường thẳng (∆) song song với (d): 4x – 3y + 3 = 0 và tiếp xúc với (C).
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Viết phương trình đường thẳng (∆) song song với (d): 4x – 3y + 3 = 0 và tiếp xúc với (C).
Câu 7:
Một bàn dài có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 4 ghế. Người ta xếp chỗ ngồi cho 4 học sinh trường A và 4 học sinh trường B vào bàn nói trên. Hỏi xác suất xếp các học sinh vào hai dãy ghế sao cho bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau?
Một bàn dài có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 4 ghế. Người ta xếp chỗ ngồi cho 4 học sinh trường A và 4 học sinh trường B vào bàn nói trên. Hỏi xác suất xếp các học sinh vào hai dãy ghế sao cho bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau?
Câu 8:
Cho mẫu số liệu sau: 11; 16; 17; 19; 20; 21; 22; 23; 23; 24; 25. Trung vị của mẫu số liệu là
Cho mẫu số liệu sau: 11; 16; 17; 19; 20; 21; 22; 23; 23; 24; 25. Trung vị của mẫu số liệu là
Câu 10:
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
Năng suất lúa (tạ/ha)
25
30
35
40
45
Tần số
4
7
9
6
5
Khoảng tứ phân vị của bảng số liệu trên là:
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
|
Năng suất lúa (tạ/ha) |
25 |
30 |
35 |
40 |
45 |
|
Tần số |
4 |
7 |
9 |
6 |
5 |
Khoảng tứ phân vị của bảng số liệu trên là:
Câu 11:
Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Khi đó phương trình đường trung trực của cạnh AB có phương trình là:
Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Khi đó phương trình đường trung trực của cạnh AB có phương trình là:
Câu 12:
Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0) và một số a < c và a > 0. Tập hợp các điểm M sao cho |MF1 – MF2| = 2a được gọi là:
Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0) và một số a < c và a > 0. Tập hợp các điểm M sao cho |MF1 – MF2| = 2a được gọi là:
Câu 13:
Trong mặt phẳng tọa độ Oxy, cho G(3; 5). Tọa độ của \(\overrightarrow {OG} \) là
Câu 14:
Cho đường tròn (C): (x – 2)2 + (y – 2)2 = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:
Cho đường tròn (C): (x – 2)2 + (y – 2)2 = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:
Câu 15:
Gieo một đồng xu ba lần liên tiếp. Xác suất để ba lần tung kết quả giống nhau là:
Gieo một đồng xu ba lần liên tiếp. Xác suất để ba lần tung kết quả giống nhau là:
