Câu hỏi:
05/11/2024 81,575
Từ một đỉnh tháp chiều cao CD=80m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là và . Ba điểm A,B.D thẳng hàng. Tính khoảng cách AB?
A. 71m
B. 91m
C. 79m
D. 40m
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là : B
- Khoảng cách AB là 91m.
Giải thích:
Lời giải
Ta có: Trong tam giác vuông CDA:
Trong tam giác vuông CDB:
Suy ra: khoảng cách
* Mở rộng:
Giải tam giác
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
– Biết độ dài ba cạnh;
– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
Ví dụ: Cho tam giác ABC có AB = 4, BC = 6, AC = . Điểm M thuộc đoạn BC sao cho MC = 2MB.
a) Tính cos các góc của tam giác ABC.
b) Tính độ dài cạnh AM.
Hướng dẫn giải:
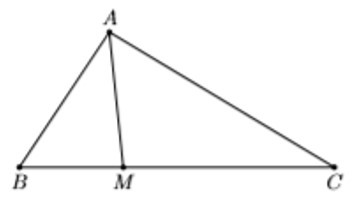
a) Theo định lí cosin trong tam giác ABC ta có:
cosB = = =
⇒ = 60°.
cosC = = =
cosA = = =
b) Ta có:
MC = 2MB ⇒ = ⇒ =
⇒ MB = BC = .6 = 2
Áp dụng định lí côsin trong tam giác AMB ta có:
AM2 = AB2 + BM2 – 2AB.BM.cosB = 42 + 22 – 2.4.2. = 12
⇒ AM = =
Ví dụ: Cho tam giác ABC có ; và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).
Hướng dẫn giải:
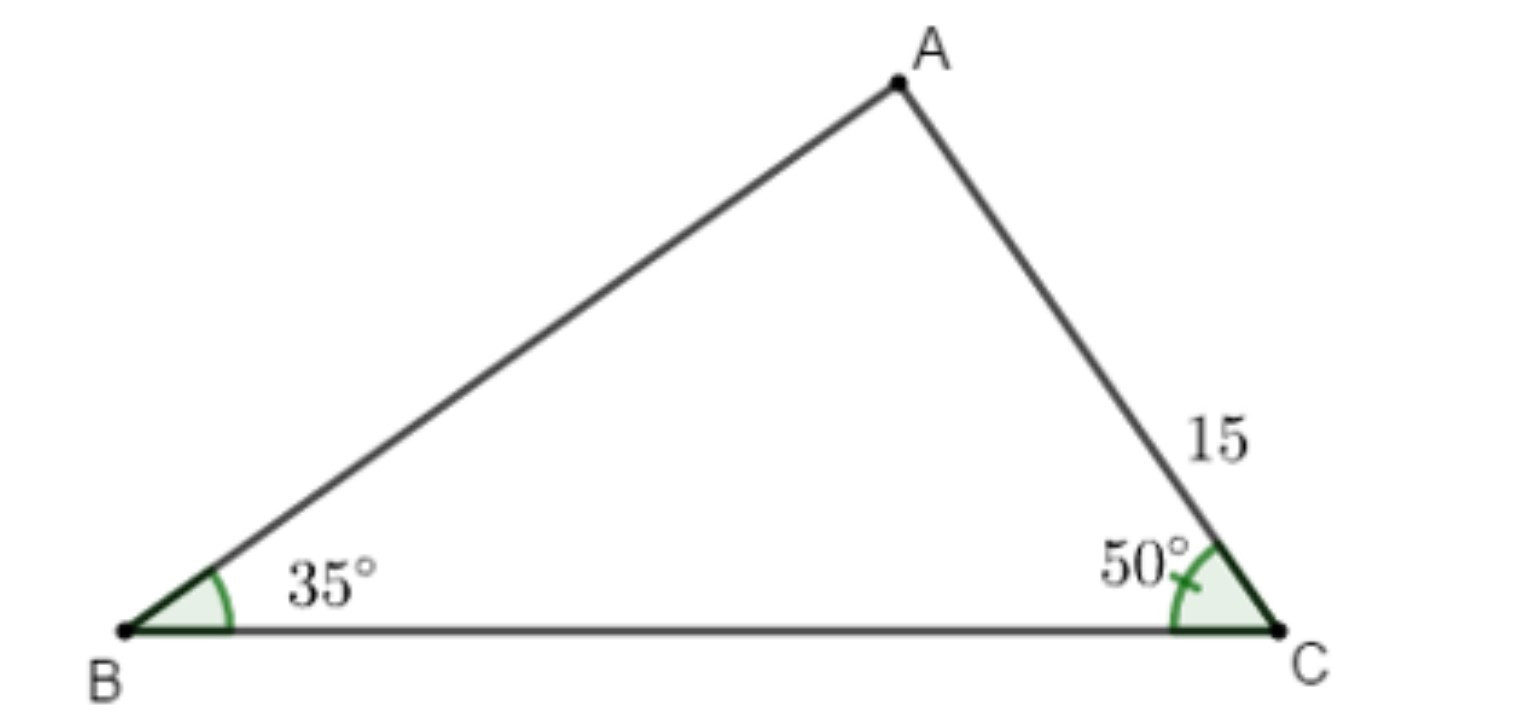
Ta có:
+ + = 180° (tổng ba góc trong tam giác)
Suy ra:
= 180° – – = 180° – 35° – 50° = 95°
Áp dụng định lí sin trong tam giác ABC ta có:
= =
Suy ra:
BC = = ≈ 26,05cm
AB = = ≈ 20,03cm
Vậy BC = 26,05cm và AB ≈ 20,03 cm.
Xem thêm các bài viết liên quan,chi tiết khác:
Lý thuyết Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác – Cánh diều


