Cho các điểm $A(1;1),B(2;4),C(10;-2).$ Góc $\widehat{BAC}$ bằng bao nhiêu?

Đáp án đúng: A

*Phương pháp giải:

- Tìm các tọa độ vecto AB và AC dựa vào dữ kiện dề bài cho 

- Tính góc BAC theo công thức định lý côsin trong tam giác

*Lời giải:

Ta có: $\overrightarrow{AB}=(1;3)$,$\overrightarrow{AC}=(9;-3)$ .

Suy ra:

$$\begin{gathered} \cos \widehat{BAC}=\frac{\left|\overrightarrow{AB}.\overrightarrow{AC}\right|}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=0 \\ \Rightarrow \widehat{BAC}={90}^0. \end{gathered}$$

* Các dạng bài tập và lý thuyết thêm 

a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

Định lí Côsin .

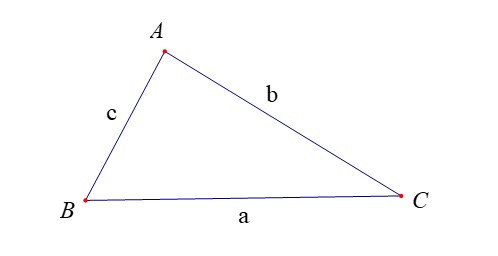
Định lí Côsin. Trong tam giác ABC:

a² = b² + c² – 2bc.cosA.

b² = c² + a² – 2ca.cosB.

c² = a² + b² – 2ab.cosC.

2. Định lí sin

Trong tam giác ABC: $\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}=\frac{\mathrm{c}}{\mathrm{sinC}}=2\mathrm{R}$.

3. Công thức tính diện tích tam giác

Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

Ta có các công thức tính diện tích tam giác ABC sau:

+) S = pr = $\frac{(\mathrm{a}+\mathrm{b}+\mathrm{c})\mathrm{r}}{2}$

+) S = $\frac{1}{2}$bc sin A = $\frac{1}{2}$ca sin B =$\frac{1}{2}$ab sin C.

+) S = $\frac{\mathrm{abc}}{4\mathrm{R}}$

+) Công thức Heron: S = $\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$.

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án)

Trắc nghiệm Giải tam giác và ứng dụng thực tế

Trắc nghiệm Toán 10. Hệ thức lượng trong tam giác có đáp án