100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao
100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P4)
-
1354 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho tam giác ABC. Biết các cạnh a, b, c đôi một khác nhau thoả mãn hệ thức: b(b2 - a2) = c(c2 - a2). Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Theo đầu bài ta có; b(b2 - a2) = c(c2 - a2)
Hay b3 - c3 = a2(b - c)
Mà b - c ≠ 0 nên b2 + bc + c2 = a2
Theo định lí côsin thì a2 = b2 + c2 - 2bccosA
Do đó: b2 + bc + c2 = b2 + c2 - 2bccosA
Suy ra: cos A = - ½ hay góc A bằng 1200.
Do đó tam giác ABC tù
Câu 2:
18/07/2024Cho tam giác ABC thỏa mãn: sinC = cosA + cosB. Tìm mệnh đề đúng
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:
Vậy sin C = cosA + cos B khi và chỉ khi
Hay
cS= (a+b)(p-a)(p-b)
c2.p.(p-a)(p-b)(p-c)=(a+b)2(p-a)2(p-b)2⇔c2.p.(p-c)=(a+b)2(p-a)(p-b)
Nên c2[(a + b) 2 - c2]= (a + b)2[ c2 - (a - b)2]
Do đó; c4 = (a2 - b2) 2
Suy ra a2 = b2 + c2 hoặc b2 = c2 + a2
Suy ra; tam giác ABC vuông tại A hoặc B.
Câu 3:
18/07/2024Cho tứ giác ABCD. Cho hai đường chéo AC và BD vuông góc với nhau. Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn D.
Ta có: AB2 + CD2 - BC2 - AD2
Do 2 đường chéo AC và BD vuông góc với nhau nên =→0
Từ đó; AB2 + CD2 - BC2 - AD2 = 0 hay AB2 + CD2 = BC2 + AD2
Câu 4:
18/07/2024Cho 4 điểm A, B, C, D thỏa mãn hệ thức AC2 + BD2 = AD2 + BC2. Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn C
Theo đầu bài ta có: AC2 + BD2 = AD2 + BC2 nên AC2 - AD2 = BC2 - BD2
Suy ra:
Hay
Tương đương
Câu 5:
22/07/2024Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho AM = AC/4, N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn D.
Đặt →AB=→x;
Do AB và AD vuông góc với nhau và AB = AD nên
Khi đó :
Ta có
Mặt khác
Vậy tam giác BMN vuông cân tại đỉnh M.
Câu 6:
18/07/2024Cho tam giác đều ABC, độ dài cạnh là 3a . Lấy M, N, P lần lượt nằm trên các cạnh BC, CA, AB sao cho BM = a; CN = 2a và AP = x . Tính x để AM vuông góc với PN.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Do AM và PN vuông góc với nhau nên
Câu 7:
18/07/2024Cho hình chữ nhật ABCD. Kẻ BK ⊥ AC. Gọi M, N lần lượt là trung điểm của AK và CD. Tìm mệnh đề đúng
 Xem đáp án
Xem đáp án
Chọn B.
Xét đáp án B
Đặt và BA = a; BC = b và BK = c.
Do M là trung điểm của AK nên ,
Do đó
Vì và
nên
Suy ra MN và BM vuông góc với nhau
Do đó góc BMN bằng 900.
Câu 8:
23/07/2024Cho hình thang vuông ABCD có đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = a. Gọi I là trung điểm của CD. Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Do I là trung điểm của DC nên ta có:
Lại có:
suy ra
Vậy AI ⊥ BD.
Câu 9:
12/07/2024Cho tam giác vuông ABC tại C có AC = 9, CB = 5. Tính
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: = AB. AC.cos BAC
Mà:
Suy ra:
Câu 10:
18/07/2024Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2). Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
 Xem đáp án
Xem đáp án
Chọn C.
Điểm D nằm trên trục Ox nên D( x; 0)
Mà: DA = DB ⇔DA2 = DB2
⇔ (2 – x)2 + 42 = (1 – x)2 + 22
⇔ 4 – 4x + x2 + 16 = 1 – 2x + x2 + 4
⇔ -2x = -15 ⇔x = 15/2. Suy ra:
Câu 11:
23/07/2024Cho hai điểm A(-3; 2), B(4; 3). Biết có 2 điểm M trên trục Ox sao cho tam giác MAB vuông tại M. Tính tổng hoành độ 2 điểm đó.
 Xem đáp án
Xem đáp án
Chọn C.
Điểm M ∈ Ox ⇒ M(x; 0).
Khi đó
ΔMAB vuông tại M nên
Hay (–3 – x)(4 – x) + 2.3 = 0
⇔ –12 + 3x – 4x + x2 + 6 = 0
⇔ x2 – x – 6 = 0 ⇔ .
Vậy: M1(3; 0), M2(-2; 0) và tổng hoành độ của chúng là : 3 + (-2) = 1.
Câu 12:
23/07/2024Cho hai điểm A(-3; 2), B(4; 3). Tìm tọa độ điểm N trên trục Oy sao cho ΔNAB cân tại N.
 Xem đáp án
Xem đáp án
Chọn D.
Điểm N ∈ Oy nên tọa độ điểm N(0; y).
Khi đó
Mà tam giác NAB cân tại N nên NA = NB ⇒ NA2 = NB2
⇔ (-3)2 + (2 – y)2 = 42 + (3 – y)2
9 + 4 – 4y + y2 = 16 + 9 – 6y + y2
⇔ 2y = 12 ⇔ y = 6
Vậy: N(0; 6).
Câu 13:
23/07/2024Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4). Tìm tọa độ trực tâm H của tam giác ABC?
 Xem đáp án
Xem đáp án
Chọn D.
Gọi H (x; y) là trực tâm tam giác ABC nên
Mà
Suy ra:
Vậy H(2; 2).
Câu 14:
23/07/2024Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4) . Tìm tọa độ điểm I là tâm đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Chọn A.
Gọi I(x; y) là tâm đường tròn ngoại tiếp ΔABC
Suy ra
Vậy I(1;2)
Câu 15:
21/07/2024Cho tam giác vuông ABC tại B, A = 620 và cạnh b = 54. Hỏi a + c gần với giá trị nào nhất?
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: là 2 góc phụ nhau nên
+ Tính b: sinA = a/b ⇒ a = b.sinA = 54.sin620 ≈ 47,68
+ Tính c: sinC = c/b ⇒ c = b.sinC = 54.sin280 ≈ 25,35
Do đó; a + c ≈ 73,03.
Câu 16:
18/07/2024Cho tam giác ABC đều . Tìm hệ thức sai?
 Xem đáp án
Xem đáp án
Chọn D.
Ta đi xét các phương án
+ Phương án A
Ta có: VP = a cosC + c cosA
+ Phương án B
Ta có: a = 2RsinA, b = 2RsinB, c = 2RsinC
mà b = a cosC + c cosA ⇒ 2RsinB = 2RsinA cosC + 2RsinC cosA
⇒ sinB = sinA cosC + sinC cosA
+ Phương án C
Ta có: S = ½. b.hb = ½.a.c.sinB nên b.hb= acsinB
Mà: a = 2RsinA, b = 2RsinB, c = 2RsinC
Suy ra: 2RsinBhb= 2RsinA.2RsinC.sinB ⇒ hb = 2RsinA sinC.
Câu 17:
18/07/2024Cho tam giác ABC có a = 7, b = 8, c = 5. Gọi AD là phân giác trong của góc A. Tính AD.
 Xem đáp án
Xem đáp án
Chọn B.
+ Tính S:
Ta có nửa chu vi tam giác là p = (7 + 8 + 5) : 2 = 10
Suy ra:
+ Tính góc A:
Ta có:
+ Tính AD:
Ta có: SABD= ½.AB. AD.sin(A/2) = ½.5.AD.sin300 = 5/4 AD
SACD= ½AC. AD.sin(A/2) = ½.8.AD.sin300 = 2AD
Mà: S = SABD+ SACD
Nên hay
suy ra
Câu 18:
21/07/2024Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:
a(a2 – c2) = b(b2 – c2) ⇔ a3 – ac2 = b3 – bc2
⇔ a3 – b3 = ac2 – bc2
⇔ (a – b)(a2 + ab + b2) = c2(a – b)
⇔ a2 + ab + b2 = c2
⇔ ab = c2 – a2 – b2
Ta lại có: 
Câu 19:
21/07/2024Cho ΔABC thỏa mãn c = 2bcosA và 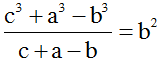 . Tìm mệnh đề đúng?
. Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
⇔ c3 + a3 – b3 = b2c + ab2 – b3
⇔ c3 + a3 = b2c + ab2
⇔ (c + a)(c2 – ca + a2) = b2(c + a)
⇔ c2 – ca + a2 = b2
⇔ c2 – ca + a2 = a2 + c2 – 2accosB
Mà: c = 2b cosA
Ta lại có a2 = b2 + c2 – 2bc cosA
⇔ a2 = b2 + c2 – 2bc. c/2b ⇔ a2 = b2 ⇔ a = b
Vậy ΔABC đều.
Câu 20:
18/07/2024Cho tam giác ABC có cạnh AB = 14, góc C = 1200, tổng hai cạnh còn lại là 16. Tính độ dài hai cạnh còn lại.
 Xem đáp án
Xem đáp án
Chọn D.
Theo định lí cosin ta có:
AB2 = BC2 + AC2 – 2.BC.AC.cos
⇔ 196 = BC2 + AC2 – 2.BC.AC.cos1200
⇔ 196 = BC2 + AC2 + BC.AC (1)
Ta lại có: BC + AC = 16 ⇒ AC = 16 – BC thay vào (1), ta được:
196 = BC2 + (16 – BC)2 + BC(16 – BC)
⇔ BC2 – 16BC + 60 = 0
* Với BC = 10 ⇒ AC = 6
* Với BC = 6 ⇒ AC = 10
Vậy: BC = 10 và AC = 6 hoặc BC = 6 và AC = 10.
Câu 21:
18/07/2024Tính giá trị biểu thức P = sin300cos150 + sin1500.cos1650
 Xem đáp án
Xem đáp án
Chọn B.
Hai góc 300 và 1500 bù nhau nên sin300 = sin1500
Hai góc 150 và 1650 bù nhau nên cos150 = -cos 1650.
Do đó P = sin300cos150+ sin1500.cos1650 = sin1500(-cos1650 + cos1650) = 0.
Câu 22:
20/07/2024Cho hai góc bù nhau α và β. Tính giá trị của biểu thức P= cosα.cosβ- sinα.sinβ.
 Xem đáp án
Xem đáp án
Chọn C.
Hai góc α và β bù nhau nên sinα = sinβ và cosα = - cosβ.
Do đó P = cosα.cosβ- sinα.sinβ.
= -cos2α – sin2α = -1
Câu 23:
13/10/2024Cho tam giác ABC. Tính P = sinA. cos(B + C) + cos A.sin(B + C).
 Xem đáp án
Xem đáp án
Đáp án đúng: A.
*Phương pháp giải:
- Sử dụng tổng 3 góc trong 1 tam giác với góc A + góc ( B+C) = 180 độ
- Áp dụng thêm tính chất về 2 góc bù nhau trong lượng giác
*Lời giải:
Giả sử A = α; B + C = β.
Biểu thức trở thành P = sinα.cosβ - cosα.sinβ.
Trong tam giác ABC, có A + B + C = 1800 nên α + β = 1800.
Do hai góc α và β bù nhau nên sinα = sinβ và cosα = - cosβ.
Do đó, P = sinα.cosβ - cosα.sinβ = -sinα.cosα + cosα.cosβ = 0.
*Một số dạng bài về hệ thức lượng trong tam giác:
Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = – cos α;
tan (180° – α) = – tan α (α ≠ 90°);
cot (180° – α) = – cot α (0° < α < 180°).
Định lí côsin
Cho tam giác ABC có BC = a, AC = b và AB = c:
a2 = b2 + c2 – 2bc.cosA; b2 = c2 + a2 – 2ca.cosB; c2 = a2 + b2 – 2ab.cosC.
Hệ quả
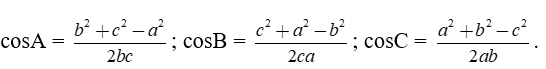
Định lí sin
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
Độ dài đường trung tuyến
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.
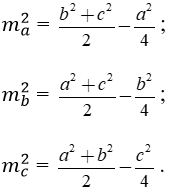
Xem thêm các bài viết liên quan hay, chi tiết
Câu 24:
20/07/2024Cho tam giác ABC. Tính P = cosA.cos( B + C) – sinA.sin(B + C).
 Xem đáp án
Xem đáp án
Chọn C.
Giả sử A = α; B + C = β. Biểu thức trở thành P = cosα.cosβ - sinα.sinβ.
Trong tam giác ABC có A + B + C = 1800 nên α + β = 1800.
Do hai góc α và β bù nhau nên sinα = sinβ và cosα = - cosβ.
Do đó P = cosα.cosβ- sinα.sinβ = -cos2α - sin2α = -1.
Câu 25:
27/11/2024Cho biết 3cosα – sinα = 1; 00 < α < 900. Giá trị của tanα bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Lời giải
Ta có 3cosα – sinα = 1 nên 3cosα = sinα + 1
Suy ra: 9cos2α = sin2α + 2sinα + 1
Hay 10sin2α + 2sinα - 8 = 0
Do đó: sinα = -1 hoặc sinα = 0,8
+ sinα = -1 không thỏa mãn vì 00 < α < 900
+ sinα = 0,8 thì cosα = 0,6 và tan α = 0,8 : 0,6 = 4/3.
*Phương pháp giải
Chuyển vế bình phương tính ra kết quả rồi đối chiéu với dữ liệu đề bài cho
*Lý thuyết
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Bài thi liên quan
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P1)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P2)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (P3)
-
25 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Hình học Ôn tập chương 2 (có đáp án) (890 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (1295 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (1353 lượt thi)
- Trắc nghiệm ôn tập chương 2 Tích vô hướng của hai vectơ và ứng dụng có đáp án (313 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Nhận biết) (305 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Thông hiểu) (302 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Vận dụng) (308 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (317 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án) (3079 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ (có đáp án) (2646 lượt thi)
- Trắc nghiệm: Giá trị lượng giác của một góc bất kì 0° đến 180° (585 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Nhận biết) (574 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Vận dụng) (546 lượt thi)
- Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án (541 lượt thi)
- Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án (516 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết) (464 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Vận dụng) (440 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu) (413 lượt thi)