Câu hỏi:
07/11/2024 200Biểu thức B = sin2x.tan2x – tan2x + sin2 x có giá trị bằng
A. -2
B. -1
C. 0
D. 1
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C.
*Lời giải:
Từ giả thiết ta suy ra:
B = tan2x (sin2x - 1) + sin2 x = -tan2x.cos2x + sin2x
*Phương pháp giải:
- áp dụng các công thức lượng giác để biến đổi rồi thực hiện phép tính tìm ra kết quả
*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:
Công thức nhân đôi:
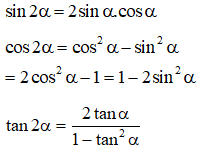
* Công thức hạ bậc:
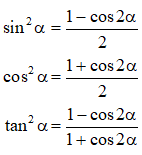
Phương trình cosx=a
- Trường hợp |a| > 1
Phương trình cosx = a vô nghiệm vì với mọi x.
- Trường hợp .
Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là:
Phương trình tanx=a
- Điều kiện xác định của phương trình là
Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là:
+) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:
Tổng quát; tan f(x) = tan g(x) .
+) Phương trình tanx = tanβ0 có các nghiệm là: .
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết
*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 (1)
Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
- Phương pháp:
Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.
Phương trình bậc hai với hàm số lượng giác
Định nghĩa.
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:
at2 + bt + c = 0
Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Phương trình lượng giác cơ bản – Toán 11
Bài tập Phương trình lượng giác cơ bản Toán 11
Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án)– Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho các véctơ có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 600. Xác định cosin góc giữa hai vectơ
Câu 5:
Cho tam giác ABC có BC = a; CA = b; AB = c. M là trung điểm của BC, D là chân đường phân giác trong góc A. Tính
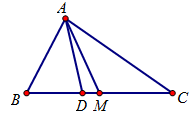
Câu 7:
Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy điểm N sao cho DN = 1 và P là trung điểm BC. Tính cosMNP?
Câu 9:
Biểu thức A = 3(sin4x + cos4x) - 2 (sin6x + cos6x) có giá trị bằng:
Câu 12:
Giá trị của biểu thức A = sin2410 + sin2450 + sin2490 + sin2450 là
Câu 13:
Trong mặt phẳng tọa độ Oxy cho các điểm A(1;2); B(-2; -4) và C(0;1); D(-1; 3/2). Mệnh đề nào sau đây đúng ?
Câu 15:
Biết sina+ cosa = . Hỏi giá trị của sin4a + cos4a bằng bao nhiêu?


