Giải Toán lớp 6 Bài 24 (Kết nối tri thức): So sánh phân số. Hỗn số dương

Giải Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương

Video giải Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương - Kết nối tri thức

Giải Toán lớp 6 trang 9 Tập 2

Toán lớp 6 trang 9 Bài toán mở đầu:

Lời giải:

Trong tình huống trên ta cần so sánh hai phân số $\frac{3}{4}$ và $\frac{5}{6}$

Sau bài học này sẽ giúp chúng ta so sánh hai phân số trên.

Toán lớp 6 trang 9 Hoạt động 1: Em thực hiện các yêu cầu sau để quy đồng mẫu hai phân số $\frac{5}{6}$ và $\frac{7}{4}$

• Tìm bội chung nhỏ nhất của hai mẫu số.
• Viết hai phân số mới bằng hai phân số đã cho và có mẫu là số vừa tìm được.

Lời giải:

+) Phân tích các số 6 và 4 ra thừa số nguyên tố, ta được:

6 = 2. 3;

4 = 2²

+) Ta thấy thừa số chung là 2; thừa số riêng là 3

+) Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 1

Khi đó BCNN(6; 4) = 2².3 = 12

Ta chọn mẫu chung của hai phân số là 12.

Ta có:

$\frac{5}{6}=\frac{5.2}{6.2}=\frac{10}{12}$ (tính chất cơ bản của phân số)

$\frac{7}{4}=\frac{7.3}{4.3}=\frac{21}{12}$ (tính chất cơ bản của phân số)

Toán lớp 6 trang 9 Hoạt động 2:Tương tự HĐ1, em hãy quy đồng mẫu hai phân số $\frac{-3}{5}$và $\frac{-1}{2}$.

Lời giải:

+) Phân tích các số 5 và 2 ra thừa số nguyên tố, ta được:

5 = 5 ; 2 = 2

+) Ta thấy không có thừa số chung; thừa số riêng là 2 và 5

+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 5 là 1

Khi đó BCNN(5, 2) = 2. 5 = 10

Ta chọn mẫu chung của hai phân số là 10.

Ta có:

$\frac{-3}{5}=\frac{(-3).2}{5.2}=\frac{(-6)}{10}$ (tính chất cơ bản của phân số)

$\frac{-1}{2}=\frac{(-1).5}{2.5}=\frac{(-5)}{10}$ (tính chất cơ bản của phân số)

Giải Toán lớp 6 trang 10 Tập 2

Toán lớp 6 trang 10 Luyện tập 1: Quy đồng mẫu các phân số:

$\frac{-3}{4}; \frac{5}{9}; \frac{2}{3}$

Lời giải:

+) Ta có: 4 = 2^2; 9 = 3²; 3 = 3

Do đó BCNN(4; 9; 3) = 2².3² = 4.9 = 36

+) Tìm thừa số phụ: 36: 4 = 9; 36: 9 = 4 và 36: 3 = 12

+) Ta có:

$\frac{-3}{4}=\frac{(-3).9}{4.9}=\frac{-27}{36}$

$\frac{5}{9}=\frac{5.4}{9.4}=\frac{20}{36}$

$\frac{2}{3}=\frac{2.12}{3.12}=\frac{24}{36}$

Toán lớp 6 trang 10 Hoạt động 3: Em hãy nhắc lại quy tắc so sánh hai phân số có cùng mẫu (tử và mẫu đều dương), rồi so sánh hai phân số $\frac{7}{11}$ và $\frac{9}{11}$.

Lời giải;

+) Quy tắc so sánh hai phân số có cùng mẫu (tử và mẫu đều dương) thì phân số nào có tử lớn hơn thì phân số đó lớn hơn.

+) Vì 7 < 9 nên $\frac{7}{11}$ < $\frac{9}{11}$.

Toán lớp 6 trang 10 Luyện tập 2:Tìm dấu thích hợp (>, <) thay cho dấu "?".

a) $\frac{-2}{9} \boxed{?} \frac{-7}{9}$

b) $\frac{5}{7} \boxed{?} \frac{-10}{7}$

Lời giải:

a) Hai phân số đã cho có chung mẫu nên ta chỉ cần so sánh tử số với nhau:

Vì 2 < 7 nên –2 > – 7

Suy ra $\frac{-2}{9}>\frac{-7}{9}$

Vậy ta điền: $\frac{-2}{9}\boxed{>}\frac{-7}{9}$

b) Hai phân số này có chung mẫu nên để so sánh thì ta chỉ cần so sánh tử số với nhau:

Vì 5 > –10 nên $\frac{5}{7}>\frac{-10}{7}$.

Vậy ta điển $\frac{5}{7} \boxed{>} \frac{-10}{7}$.

Toán lớp 6 trang 10 Hoạt động 4: Tình huống mở đầu:

Đề giải quyết tình huống mở đầu, ta cần so sánh $\frac{3}{4}$ và $\frac{5}{6}$. Em hãy thực hiện các yêu cầu sau:

• Viết hai phân số trên dưới dạng hai phân số có cùng một mẫu dương bằng cách quy đồng mẫu số.
• So sánh hai phân số cùng mẫu vừa nhận được. Từ đó kết luận về phần bánh còn lại của hai bạn Vuông và Tròn.

Lời giải:

Ta có: 4 = 2^2; 6 = 2. 3

Do đó BCNN(4; 6) = 2².3 = 4.3 = 12

+) Thừa số phụ: 12: 4 = 3; 12: 6 = 2

$\frac{3}{4}=\frac{3.3}{4.3}=\frac{9}{12}$

$\frac{5}{6}=\frac{5.2}{6.2}=\frac{10}{12}$

Vì 9 < 10 nên $\frac{9}{12}<\frac{10}{12}$ hay $\frac{3}{4}<\frac{5}{6}$.

Vậy phần bánh còn lại của Tròn nhiều hơn phần bánh còn lại của Vuông.

Toán lớp 6 trang 10 Luyện tập 3: So sánh các phân số sau:

Lời giải:

a) Ta có: 10 = 2. 5; 15 = 3. 5

Khi đó BCNN(10; 15) = 2. 3. 5 = 30

Thừa số phụ: 30: 10 = 3; 30: 15 = 2

+) $\frac{7}{10}=\frac{7.3}{10.3}=\frac{21}{30}$

+) $\frac{11}{15}=\frac{11.2}{15.2}=\frac{22}{30}$

Vì 21 < 22

nên $\frac{21}{30}<\frac{22}{30}$

hay $\frac{7}{10}<\frac{11}{15}$

Vậy $\frac{7}{10}<\frac{11}{15}$.

b) Ta có nên BCNN(8; 24) = 24

Thừa số phụ: 24: 8 = 3; 24: 24 = 1

+) $\frac{-1}{8}=\frac{(-1).3}{8.3}=\frac{-3}{24}$

+) $\frac{-5}{24}=\frac{-5}{24}$

Vì 3 < 5 nên –3 > –5

nên $\frac{-3}{24}>\frac{-5}{24}$

hay $\frac{-1}{8}>\frac{-5}{24}$.

Vậy $\frac{-1}{8}>\frac{-5}{24}$.

Giải Toán lớp 6 trang 11 Tập 2

Toán lớp 6 trang 11 Thử thách nhỏ:

Không quy đồng mẫu số, em hãy so sánh $\frac{31}{32}$ và $\frac{-5}{57}$.

Lời giải:

+) Vì 31 và 32 là hai số nguyên cùng dấu khác 0 nên $\frac{31}{32}>0$ (1)

+) Vì –5 và 57 là hai số nguyên trái dấu khác 0 nên $\frac{-5}{57}<0$ (2)

Từ (1) và (2) ta có: $\frac{31}{32}>\frac{-5}{57}$

Vậy $\frac{31}{32}>\frac{-5}{57}$

Toán lớp 6 trang 11 Hoạt động 5:

Viết phân số biểu thị phần bánh của mỗi bạn.

Lời giải:

Chia đều ba cái bánh cho hai bạn thì mỗi bạn được số phần bánh là:

3: 2 = $\frac{3}{2}$ (bánh)

Vậy mỗi bạn được $\frac{3}{2}$ bánh.

Toán lớp 6 trang 11 Hoạt động 6:

Tròn nói mỗi bạn được 1 cái bánh và $\frac{1}{2}$ cái bánh. Em có đồng ý với Tròn không?

Lời giải:

Em đồng ý với Tròn vì có ba cái bánh, mỗi bạn được 1 cái bánh thì còn 1 cái bánh, chia đều cho 2 bạn thì mỗi bạn được $\frac{1}{2}$ cái bánh nữa.

Vậy Tròn nói mỗi bạn được 1 cái bánh và $\frac{1}{2}$ cái bánh là đúng.

Giải Toán lớp 6 trang 12 Tập 2

Toán lớp 6 trang 12 Câu hỏi: $2\frac{5}{4}$ có là một hỗn số không? Vì sao?

Lời giải:

Ta có phân số $\frac{5}{4}$ có 5 > 4 > 0 nên $\frac{5}{4}>\frac{4}{4}=1$.

Vậy $2\frac{5}{4}$ không là một hỗn số vì phần phân số lớn hơn 1.

Toán lớp 6 trang 12 Câu hỏi:

a) Viết phân số $\frac{24}{7}$ dưới dạng hỗn số;

b) Viết hỗn số $5\frac{2}{3}$ dưới dạng phân số.

Lời giải:

a)

$\to \frac{24}{7}=3+\frac{3}{7}=3\frac{3}{7}$

b) $5\frac{2}{3}=\frac{5.3+2}{3}=\frac{15+2}{3}=\frac{17}{3}$

Toán lớp 6 trang 12 Bài 6.8: Quy đồng mẫu các phân số sau:

a) $\frac{2}{3}$ và $\frac{-6}{7}$

b) $\frac{5}{2^2{.3}^2}$ và $\frac{-7}{2^2.3}$

Lời giải:

a)

Tìm mẫu chung: BCNN(3, 7) = 3. 7 = 21

Tìm thừa số phụ: 21: 3 = 7; 21: 7 = 3

Ta có:

+) $\frac{2}{3}=\frac{2.7}{3.7}=\frac{14}{21}$

+) $\frac{-6}{7}=\frac{(-6).3}{7.3}=\frac{-18}{21}$

b)

Tìm mẫu chung: BCNN(2².3²; 2².3) = 2².3²= 4. 9 = 36

Tìm thừa số phụ: 36: (2².3²) = 36: 36 = 1;

36: (2².3) = 36: 12 = 3

Ta có:

+) $\frac{5}{2^2{.3}^2}=\frac{5}{36}$

+) $\frac{-7}{2^2.3}=\frac{7}{12}=\frac{7.3}{12.3}=\frac{21}{36}$

Toán lớp 6 trang 12 Bài 6.9:So sánh các phân số sau:

a) $\frac{-11}{8}$ và $\frac{1}{24}$

b) $\frac{3}{20}$ và $\frac{6}{15}$

Lời giải:

a)

Cách 1: Vì nên BCNN(8; 24) = 24. Suy ra MTC = 24.

+) $\frac{-11}{8}=\frac{(-11).3}{8.3}=\frac{-33}{24}$

+) $\frac{1}{24}$

Vì –33 < 1 nên $\frac{-33}{24}<\frac{1}{24}$ hay $\frac{-11}{8}<\frac{1}{24}$

Vậy $\frac{-11}{8}<\frac{1}{24}$

Cách 2:

Phân số có tử số là –11 < 0 và mẫu số là 8 > 0 nên $\frac{-11}{8}<0$;

Phân số có tử và mẫu số đều dương nên $\frac{1}{24}>0$.

Do đó $\frac{-11}{8}<\frac{1}{24}$.

Vậy $\frac{-11}{8}<\frac{1}{24}$.

b) Ta có 20 = 2².5 ; 15 = 3.5

Ta chọn mẫu chung là

BCNN(20; 15) = 2².3.5 = 60

Tìm thừa số phụ: 60: 20 = 3; 60: 15 = 4

+) $\frac{3}{20}=\frac{3.3}{20.3}=\frac{9}{60}$

+) $\frac{6}{15}=\frac{6.4}{15.4}=\frac{24}{60}$

Vì 9 < 24 nên $\frac{9}{60}<\frac{24}{60}$ hay $\frac{3}{20}<\frac{6}{15}$

Vậy $\frac{3}{20}<\frac{6}{15}$

Toán lớp 6 trang 12 Bài 6.10: Lớp 6A có $\frac{4}{5}$ số học sinh thích bóng bàn, $\frac{7}{10}$ số học sinh thích bóng đá và $\frac{1}{2}$ số học sinh thích bóng chuyền. Hỏi môn thể thao nào được các bạn học sinh lớp 6A yêu thích nhất?

Lời giải:

Vì $10⋮ 2; 10 ⋮5$nên BCNN(5; 10; 2) = 10

Suy ra MTC = 10.

Tìm thừa số phụ 10: 5 = 2; 10: 2 = 5

Ta có:

$\frac{4}{5}=\frac{4.2}{5.2}=\frac{8}{10}$

$\frac{1}{2}=\frac{1.5}{2.5}=\frac{5}{10}$

$\frac{7}{10}$

Vì 5 < 7 < 8 nên $\frac{5}{10}<\frac{7}{10}<\frac{8}{10}$ hay $\frac{1}{2}<\frac{7}{10}<\frac{4}{5}$ do đó môn bóng bàn là môn thể thao được học sinh lớp 6A yêu thích nhất.

Vậy môn bóng bàn là môn thể thao được học sinh lớp 6A yêu thích nhất

Toán lớp 6 trang 12 Bài 6.11:

a) Khối lượng nào lớn hơn: $\frac{5}{3}$kg hay $\frac{15}{11}$kg?

b) Vận tốc nào nhỏ hơn: $\frac{5}{6}$km/h hay $\frac{4}{5}$km/h

Lời giải:

a)

Tìm mẫu chung: BCNN(3; 11) = 33

Tìm thừa số phụ: 33: 3 = 11; 33: 11 = 3

+) $\frac{5}{3}=\frac{5.11}{3.11}=\frac{55}{33}$

+) $\frac{15}{11}=\frac{15.3}{11.3}=\frac{45}{33}$

Vì 55 > 45 nên $\frac{55}{33}>\frac{45}{33}$ hay $\frac{5}{3}>\frac{15}{11}$

Vậy $\frac{5}{3}$kg > $\frac{15}{11}$kg.

b)

Tìm mẫu chung: BCNN(6; 5) = 30

Tìm thừa số phụ: 30:6 = 5; 30:5 = 6

+) $\frac{5}{6}=\frac{5.5}{6.5}=\frac{25}{30}$

+) $\frac{4}{5}=\frac{4.6}{5.6}=\frac{24}{30}$

Vì 25 > 24 nên $\frac{25}{30}>\frac{24}{30}$ hay $\frac{5}{6}>\frac{4}{5}$

vì thế $\frac{4}{5}<\frac{5}{6}$

Vậy $\frac{4}{5}$km/h < $\frac{5}{6}$km/h

Toán lớp 6 trang 12 Bài 6.12: Bảng sau cho biết chiều dài (theo đơn vị feet, 1 feet xấp xỉ bằng 30,48 cm) của một số loài động vật có vú nhỏ nhất trên thế giới.

(Theo Scholastic Book of World Records)

Hãy sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé.

Lời giải:

Ta có:

12 = 2².3

100 = 2².5²

4 = 2²

3 = 3

Tìm mẫu chung:

BCNN(12, 100, 4, 3) =5².2².3=300

Tìm thừa số phụ:

300: 12 = 25;

300: 100 = 3;

300: 4 = 75;

300: 3 = 100

+) $\frac{5}{12}=\frac{5.25}{12.25}=\frac{125}{300}$

+) $\frac{83}{100}=\frac{83.3}{100.3}=\frac{249}{300}$

+) $\frac{1}{4}=\frac{1.75}{4.75}=\frac{75}{300}$

+) $\frac{1}{3}=\frac{1.100}{3.100}=\frac{100}{300}$

Vì 75 < 100 < 125 < 249

nên $\frac{75}{300}<\frac{100}{300}<\frac{125}{300}<\frac{249}{300}$

hay $\frac{1}{4}<\frac{1}{3}<\frac{5}{12}<\frac{83}{100}$

vì thế $\frac{83}{100}>\frac{5}{12}>\frac{1}{3}>\frac{1}{4}$

Do đó sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé: Dơi Kitti; Chuột chũi châu Âu, Sóc chuột phương Đông, Chuột túi có gai.

Toán lớp 6 trang 12 Bài 6.13:Mẹ có 15 quả táo, mẹ muốn chia đều số quả táo đó cho bốn anh em. Hỏi mỗi anh em được mấy quả táo và mấy phần của quả táo?

Lời giải:

Mẹ có 15 quả táo chia đều cho bốn anh em thì mỗi anh em sẽ được $\frac{15}{4}$ táo.

Ta có: $\frac{15}{4}=3+\frac{3}{4}=3\frac{3}{4}$

Vậy mỗi anh em được 3 quả và $\frac{3}{4}$ quả táo

Bài giảng Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương - Kết nối tri thức

Lý thuyết Toán 6 Bài 24: So sánh phân số. Hỗn số dương - Kết nối tri thức

1. Quy đồng mẫu nhiều phân số

Để quy đồng hai hay nhiều phân số ta làm như sau:

Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.

Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Ví dụ 1: Để quy đồng ba phân số 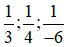ta làm như sau:

+ Đưa về các phân số có mẫu dương: .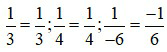

+ Tìm mẫu chung: BCNN (3; 4; 6) = 12

+ Thừa số phụ:

12 : 3 = 4

12 : 4 = 3

12 : 6 = 2

Ta có:

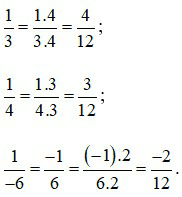
2. So sánh hai phân số

a) So sánh hai phân số cùng mẫu

– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Ví dụ 2: 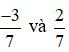là hai phân số có cùng mẫu số dương.

Vì –3 < 2 nên .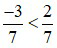

b) So sánh hai phân số không cùng mẫu

– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

Ví dụ 3: So sánh hai phân số sau: .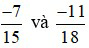

BCNN (15; 18) = 90

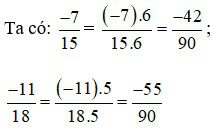
Vì –42 > –55 nên do đó,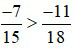

3. Hỗn số dương

– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi 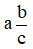là một hỗn số dương với a là phần nguyên và là phần phân số.

Ví dụ 4:

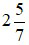là một hỗn số dương với phần nguyên là 2 và phần phân số là 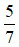. Khi đó ta đọc 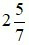là hai năm phần bảy.

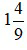là một hỗn số dương với phần nguyên là 1 và phần phân số là 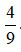. Khi đó ta đọc 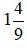là một bốn phần chín.

– Muốn đổi từ hỗn số sang phân số ta làm như sau:

Bước 1: Giữ nguyên phần mẫu số.

Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.

Ví dụ 5: Đổi hỗn số 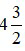sang phân số:

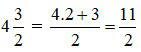
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:

Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.

Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.

Ví dụ 6: Đổi phân số 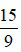sang hỗn số

Ta có 15 chia 9 được thương là 1 và dư 6 do đó:

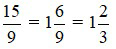
Xem thêm lời giải bài tập Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Luyện tập chung

Bài 25: Phép cộng và phép trừ phân số

Bài 26: Phép nhân và phép chia phân số

Bài 27: Hai bài toán về phân số

Luyện tập chung

Xem thêm tài liệu Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 24: So sánh phân số. Hỗn số dương