Giải Toán 6 Bài 28 ( Kết nối tri thức): Số thập phân

Giải Toán 6 Bài 28: Số thập phân

Giải Toán 6 trang 29 Tập 2

Toán lớp 6 trang 29 Hoạt động 1: Viết các phân số thập phân $\frac{17}{10}; \frac{34}{100}; \frac{25}{1000}$ dưới dạng số thập phân.

Lời giải:

Viết các phân số thập phân dưới dạng số thập phân là:

• $\frac{17}{10}=1,7$
• $\frac{34}{100}=0,34$
• $\frac{25}{1000}=0,025$

Toán lớp 6 trang 29 Hoạt động 2: Viết các số đối của các phân số thập phân trên.

Lời giải:

+) Số đối của $\frac{17}{10}$ là $\frac{-17}{10}$

+) Số đối của $\frac{34}{100}$ là $\frac{-34}{100}$

+) Số đối của $\frac{25}{1 000}$ là $\frac{-25}{1 000}$

Toán lớp 6 trang 29 Câu hỏi:Em hãy chỉ ra các số thập phân xuất hiện trong đoạn tin Hình 7.1a và Hình 7. 1b. Tìm số đối của các số thập phân đó.

Lời giải:

+) Các số thập phân suất hiện trong hình 7.1 a là: 29,96; 14,26; 7,5; 3,4.

Số đối của 29,96 là –29,96;

Số đối của 14,26 là –14,26;

Số đối của 7,5 là –7,5;

Số đối của 3,4 là –3,4.

+) Các số thập phân suất hiện trong hình 7.1 b là: –4,2; –2,4.

Số đối của –4,2 là 4,2;

Số đối của –2,4 là 2,4.

Toán lớp 6 trang 29 Luyện tập 1:

1.Viết các phân số thập phân $\frac{-5}{1000};-\frac{798}{10}$ dưới dạng số thập phân rồi tìm số đối của các số thập phân đó.

2. Viết các số thập phân xuất hiện trong đoạn tin Hình 7.1b dưới dạng phân số thập phân.

Lời giải:

1. Ta có

• $\frac{-5}{1000}=-0,005$; số đối của –0,005 là 0,005.
• $\frac{798}{10}=79,8$; số đối của 79,8 là –79,8.

2. Các số thập phân suất hiện trong hình 7.1 b là: –4,2; –2,4.

Ta có:

• $-4,2=\frac{-42}{10}$
• $-2,4=\frac{-24}{10}$

Giải Toán 6 trang 30 Tập 2

Toán lớp 6 trang 30 Luyện tập 2: Sắp xếp các số sau theo thứ tự từ bé đến lớn: 0; –8,152; 0,12; –8,9.

Lời giải:

Vì 8,9 > 8,152 nên –8,9 < –8,152

Ta lại có –8,152 < 0 < 0,12

Do đó –8,9 < –8,152 < 0 < 0,12

Vậy sắp xếp các số theo thứ tự từ bé đến lớn là: –8,9; –8,152; 0; 0,12.

Toán lớp 6 trang 30 Vận dụng: Đọc đoạn tin trong Hình 7.1b và cho biết trong hai thời điểm, 19 giờ ngày 2–1–2016 và 6 giờ ngày 25–1–2016, thời điểm nào nhiệt độ tại Pha Đin (Điện Biên) xuống thấp hơn.

Lời giải:

Vì 4,2 > 2,4 nên –4,2 < –2, 4 nên thời điểm 6 giờ ngày 25–1–2016 nhiệt độ thấp hơn thời điểm 19 giờ ngày 24 – 11 – 2016.

Vậy thời điểm 6 giờ ngày 25 – 1 – 2016 nhiệt độ tại Pha Đin (Điện Biên) xuống thấp hơn.

Toán lớp 6 trang 30 Bài 7.1:

a) Viết các phân số thập phân sau dưới dạng số thập phân.

$\frac{21}{10}; \frac{-35}{ 10}; \frac{-125}{100}; \frac{-89}{1000}$

b) Chỉ ra các số thập phân âm viết được trong câu a.

Lời giải:

a)

• $\frac{21}{10}=2,1$
• $\frac{-35}{10}=-3,5$
• $\frac{-125}{100}=-1,25$
• $\frac{-89}{1000}=-0,089$

b) Các số thập phân âm viết được trong câu a là: –3,5; –1,25; –0,089.

Toán lớp 6 trang 30 Bài 7.2: Tìm số đối của các số thập phân sau:

–1,2; 4,15; 19,2.

Lời giải:

+) Số đổi của –1,2 là 1,2;

+) Số đổi của 4,15 là –4,15;

+) Số đối của 19,2 là –19,2.

Toán lớp 6 trang 30 Bài 7.3: So sánh các số sau:

a) –421,3 và 0,15;

b) –7,52 và –7,6.

Lời giải:

a. Vì –421,3 < 0; 0,15 > 0 nên –421,3 < 0,15

Vậy –421,3 < 0,15.

b. Vì 7,52 < 7,6 nên –7,52 > –7,6.

Vậy –7,52 > –7,6.

Toán lớp 6 trang 30 Bài 7.4: Nhiệt độ đông đặc của một chất là nhiệt độ mà tại đó chất chuyển từ thể lỏng sang thể rắn.

Nhiệt độ đông đặc của rượu, nước và thuỷ ngân lần lượt là:

–117°C; 0°C; –38,83°C.

Hãy sắp xếp nhiệt độ đông đặc của ba chất này theo thứ tự từ bé đến lớn.

Lời giải:

Vì 117 > 38,83 nên –117 < –38,83

Mà –38,83 < 0 do đó –117 < –38,83 < 0

Vậy nhiệt độ của ba chất theo thứ tự từ nhỏ đến lớn là: rượu; thủy ngân; nước.

Lý thuyết Toán 6 Bài 28: Số thập phân - Kết nối tri thức

1. Phân số thập phân và số thập phân

a) Phân số thập phân.

– Phân số thập phân là phân số có phần mẫu số là lũy thừa của 10

Ví dụ 1: 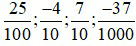… được gọi là các phân số thập phân

Các phân số 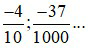là các phân số thập phân âm.

Các phân số 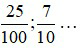là các phân số thập phân dương.

b) Số thập phân

Ta viết 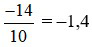là số thập phân âm, đọc là “âm một phẩy bốn”.

Ta viết 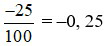là số thập phân âm, đọc là “âm không phẩy hai mươi lăm”.

Ta viết 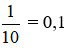là số thập phân dương, đọc là “không phẩy một”.

– Các số –0,3; –1,6; –3.76… là các số thập phân âm.

– Các số 0,17; 1, 89; 3, 15… là các số thập phân dương.

– Các số thập phân âm và và các số thập phân dương gọi chung là các số thập phân.

– Các số 1, 7 và –1, 7; 3, 2 và –3, 2… gọi là hai số đối nhau.

c) Tính chất của số thập phân

- Mỗi số thập phân gồm: Phần số nguyên viết bên trái dấu “,”; phần thập phân viết bền phải dấu “,”.

- Nếu thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì số thập phân không đổi:

21, 45 = 21, 450 = 21, 4500 = …

- Hai số thập phân được gọi là đối nhau nếu tổng của chúng bằng 0.

d) Đổi từ số thập phân ra phân số và ngược lại.

– Đổi từ số thập phân sang phân số ta làm như sau:

Bước 1: Đếm xem có bao nhiêu số ở phía bên phải dấu phẩy. Gọi n là số chữ số ở phía bên phải dấu phẩy.

Bước 2: Bỏ đi dấu phẩy và viết số không có dấu phẩy ở tử số; lũy thừa 10ⁿ ở mẫu số.

Bước 3: Rút gọn phân số phía trên để được phân số tối giãn.

Ví dụ 2: Đổi 0, 14 sang phân số ta làm như sau:

Ta đếm thấy bên phải dấu phẩy của số 0, 14 có 2 số là 1 và 4. Số 0, 14 sau khi bỏ dấu phẩy là 14

Vậy đổi 0, 14 ra phân số thập phân là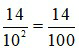

Ta rút gọn phân số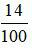

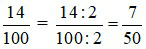
– Đổi phân số ra số thập phân

Bước 1: Đưa phân số về dạng phân số thập phân có mẫu là lũy thừa của 10

Bước 2: Kiểm tra xem mẫu số là lũy thừa mấy của 10. Giả sử mẫu số là lũy thừa bậc n của 10.

Bước 3: Đếm từ phải sang tới số thứ n của tử và đặt dấu phẩy ở đó, số thập phân cần tìm là số ở tử khi đã đặt dấu phẩy

Ví dụ 3: Đổi 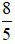ra số thập phân

Ta có: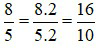

Mẫu số là lũy thừa cơ số 1 của 10.

Ta đếm từ phải sang và đặt dấu phẩy trước số thứ nhất của tử ta được 1, 6

Vậy đổi 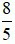sang số thập phân ta được kết quả là 1, 6.

2. So sánh hai số thập phân

a) So sánh hai số thập phân dương

Muốn so sánh hai số thập phân ta có thể làm như sau:

– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

Ví dụ 4: So sánh

a) 3, 56 và 7,37

b) 4,25 và 4,35

Lời giải:

a) Ta so sánh phần nguyên: Ta thấy 3 < 7 nên 3, 56 < 7,37

b) Ta so sánh phần nguyên: Ta thấy 4 = 4 do đó ta chuyển sang so sánh phần thập phân, bắt đầu từ phần mười:

Ta thấy 2 < 3 nên 4, 25 < 4, 35.

b) So sánh hai số thập phân âm

– Nếu a, b là hai số thập phân dương và a > b thì –a < –b

Chú ý: Số thập phân âm luôn nhỏ hơn 0 và nhỏ hơn số thập phân dương.

Số thập phân dương luôn lớn hơn 0 và lớn hơn số thập phân âm.

Ví dụ 5: So sánh

a) 0, 745 và –1, 234

b) –2, 13 và –3, 12

Lời giải:

a) 0, 745 và –1, 234

Vì 0, 745 là số thập phân dương và –1, 234 là số thập phân âm nên 0, 745 > –1, 234.

b) –2, 13 và –3, 12

Ta đi so sánh 2, 13 và 3, 12

Vì 2 < 3 nên 2, 13 < 3, 12 nên –2, 13 > –3, 12.

Xem thêm lời giải bài tập Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Bài 29: Tính toán với số thập phân

Bài 30: Làm tròn và ước lượng

Bài 31: Một số bài toán về tỉ số và tỉ số phần trăm

Luyện tập chung

Bài tập cuối Chương 7

Xem thêm tài liệu Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 28: Số thập phân