Giải Toán lớp 6 Bài 15 (Kết nối tri thức): Quy tắc dấu ngoặc

Giải Toán lớp 6 Bài 15: Quy tắc dấu ngoặc

Video giải Toán lớp 6 Bài 15: Quy tắc dấu ngoặc - Kết nối tri thức

Giải Toán lớp 6 trang 67 Tập 1

Toán lớp 6 trang 67 Câu hỏi: Viết tổng sau dưới dạng không có dấu ngoặc rồi tính giá trị của nó:

( – 23) – 15 – ( –23) + 5 + ( –10)

Lời giải:

( – 23) – 15 – ( –23) + 5 + ( –10)

= – 23 – 15 + 23 + 5 – 10

= (– 23 + 23) + (– 15 + 5 – 10)

= 0 + ( – 10 – 10 )

= 0 + ( -20)

= 0 – 20

= – 20

Toán lớp 6 trang 67 Hoạt động 1: Tính và so sánh kết quả của:

a) 4 + (12 – 15) và 4 + 12 – 15;

b) 4 – (12 – 15) và 4 – 12 + 15.

Lời giải:

a) Ta có:

4 + (12 – 15) = 4 + (– 3) = 4 – 3 = 1

4 + 12 – 15 = 16 – 15 = 1

Vì 1 = 1 nên 4 + (12 – 15) = 4 + 12 – 15

Vậy 4 + (12 – 15) = 4 + 12 – 15

b) Ta có:

4 – (12 – 15) = 4 – [– (15 – 12)] = 4 – (– 3) = 4 + 3 = 7

4 – 12 + 15 = – (12 – 4) + 15 = (– 8) + 15 = 15 – 8 = 7

Vì 7 = 7 nên 4 – (12 – 15) = 4 – 12 + 15

Toán lớp 6 trang 67 Hoạt động 2: Hãy nhận xét về sự thay đổi dấu của các số hạng trong dấu ngoặc trước và sau khi bỏ dấu ngoặc.

Lời giải:

Nhận xét:

+) Khi bỏ dấu ngoặc có dấu " + " đằng trước, dấu của các số hạng trong dấu ngoặc trước và sau khi bỏ dấu ngoặc được giữ nguyên.

+) Khi bỏ dấu ngoặc có dấu " – " đằng trước, dấu của các số hạng trong dấu ngoặc trước và sau khi bỏ dấu ngoặc thay đổi: dấu " + " đổi thành " – " và dấu " – " đổi thành " + ".

Giải Toán lớp 6 trang 68 Tập 1

Toán lớp 6 trang 68 Luyện tập 1: Bỏ dấu ngoặc rồi tính các tổng sau:

a) (–385 + 210) + (385 – 217)

b) (72 – 1 956) – (–1 956 + 28)

Lời giải:

a) (–385 + 210) + (385 – 217)

= –385 + 210 + 385 – 217 (bỏ ngoặc tròn)

= (– 385 + 385) – (217 – 210)

= 0 – 7

= –7

b) (72 – 1 956) – (–1 956 + 28)

= 72 – 1 956 + 1 956 – 28 (bỏ ngoặc tròn)

= (1 956 – 1 956) + (72 – 28)

= 0 + 44

= 44

Toán lớp 6 trang 68 Luyện tập 2: Tính một cách hợp lí:

a) 12 + 13 + 14 – 15 – 16 – 17

b) (35 – 17) – (25 – 7 + 22)

Lời giải:

a) 12 + 13 + 14 – 15 – 16 – 17

= (12 – 15) + (13 – 16) + (14 –17)

= (–3) + (–3) + (–3)

= – (3 + 3 + 3)

= – 9

b) (35 – 17) – (25 – 7 + 22)

= 35 – 17 – 25 + 7 – 22

= (35 – 25) – (17 – 7) – 22

= 10 – 10 – 22

= 0 – 22

= – 22.

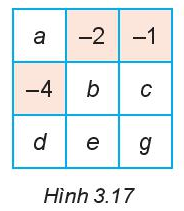
Toán lớp 6 trang 68 Thử thách nhỏ: Cho bảng 3 x 3 vuông như Hình 3. 17.

a) Biết rằng tổng các số trong mỗi hàng, mỗi cột, mỗi đường chéo đều bằng 0. Tính tổng các số trong bảng đó.

b) Hãy thay các chữ cái trong bảng bởi số thích hợp sao cho tổng các số trong mỗi hàng, mỗi cột, mỗi đường chéo đều bằng 0

Lời giải:

a) Vì tổng các số trong mỗi hàng bằng 0 nên: a + (–2) + (–1) = 0 hay a – 2 – 1 = 0 (1)

(–4) + b + c = 0 (2)

d + e + g = 0 (3)

Cộng vế với vế của (1), (2) và (3) ta được:

a + (– 2) + (– 1) + (–4) + b + c + d + e + g = 0 + 0 + 0 = 0

Vậy tổng tất cả các số trong bảng đó bằng 0.

b) Vì a – 2 – 1 = 0 (theo (1)) nên a – 3 = 0 hay a = 3

Vì tổng các số trong hàng dọc bằng 0 nên a + (–4) + d = 0 (4)

Thay a = 3 vào (4) ta được:

3 + (–4) + d = 0

3 – 4 + d = 0

–1 + d = 0

d = 0 + 1

d = 1

Vì tổng các số trong đường chéo bằng 0 nên d + b + (–1) = 0 (5)

Thay d = 1 vào (5) ta được:

1 + b + (–1) = 0

b = 0

Vì tổng các số trong hàng ngang bằng 0 nên (–4) + b + c = 0(6)

Thay b = 0 vào (6) ta được:

(–4) + 0 + c = 0

c – 4 = 0

c = 0 + 4

c = 4

Vì tổng các số trong đường chéo bằng 0 nên a + b + g = 0 (7)

Thay a = 3, b = 0 vào (7) ta được:

3 + 0 + g = 0

g + 3 = 0

g = 0 – 3 = –3

Vì tổng các số trong hàng dọc bằng 0 nên –2 + b + e = 0 (8)

Thay b = 0 vào 8 ta được:

–2 + 0 + e = 0

e – 2 = 0

e = 0 + 2 = 2

Vậy a = 3; b = 0; c = 4; d = 1; e = 2; g = –3.

Toán lớp 6 trang 68 Bài 3.19: Bỏ dấu ngoặc và tính các tổng sau:

a) – 321 + (–29) – 142 – (–72)

b) 214 – (–36) + (–305)

Lời giải:

a) – 321 + (–29) – 142 – (–72)

= – 321 – 29 – 142 + 72

= – (321 + 29) – (142 – 72)

= – 350 – 70

= – (350 + 70)

= – 420

b) 214 – (–36) + (–305)

= 214 + 36 – 305

= 250 – 305

= – (305 – 250)

= –55

Toán lớp 6 trang 68 Bài 3.20: Tính một cách hợp lí:

a) 21 – 22 + 23 – 24

b) 125 – (115 – 99)

Lời giải:

a) 21 – 22 + 23 – 24

= (21 – 22) + (23 – 24)

= (–1) + (–1)

= – (1 + 1)

= –2

b) 125 – (115 – 99)

= 125 – 115 + 99

= (125 – 115) + 99

= 10 + 99

= 109

Toán lớp 6 trang 68 Bài 3.21: Bỏ dấu ngoặc rồi tính:

a) (56 – 27) – (11 + 28 – 16)

b) 28 + (19 – 28) – (32 – 57)

Lời giải:

a) (56 – 27) – (11 + 28 – 16)

= 56 – 27 – 11 – 28 + 16

= (56 + 16) – (27 + 11 + 28)

= 72 – (38 + 28)

= 72 – 66

= 6

b) 28 + (19 – 28) – (32 – 57)

= 28 + 19 – 28 – 32 + 57

= (28 – 28) + (19 + 57) – 32

= 0 + 76 – 32

= 76 – 32

= 44

Toán lớp 6 trang 68 Bài 3.22: Tính một cách hợp lí

a) 232 – (581 + 132 – 331)

b) [12 + (–57)] – [– 57 – (–12)]

Lời giải:

a) 232 – (581 + 132 – 331)

= 232 – 581 – 132 + 331

= (232 – 132) – (581 – 331)

= 100 – 250

= – (250 – 100)

= –150

b) [12 + (–57)] – [– 57 – (–12)]

= (12 – 57) – (– 57 + 12)

= 12 – 57 + 57 – 12

= (12 – 12) + (57 – 57)

= 0 + 0

= 0

Toán lớp 6 trang 68 Bài 3.23: Tính giá trị của các biểu thức sau:

a) (23 + x) – (56 – x) với x = 7;

b) 25 – x – (29 + y – 8) với x = 13, y = 11.

Lời giải:

a) Với x = 7

(23 + x) – (56 – x)

= (23 + 7) – (56 – 7)

= 30 – 49

= – (49 – 30)

= – 19

b) Với x = 13, y = 11

25 – x – (29 + y – 8)

= 25 – 13 – (29 + 11 – 8)

= 25 – 13 – 29 – 11 + 8

= (25 + 8) – (29 + 11 + 13)

= 33 – (40 + 13)

= 33 – 53

= – (53 – 33)

= – 20

Bài giảng Toán lớp 6 Bài 15: Quy tắc dấu ngoặc - Kết nối tri thức

Lý thuyết Toán 6 Bài 15: Quy tắc dấu ngoặc – Kết nối tri thức

Bỏ dấu ngoặc trong trường hợp đơn giản

Các số âm (hay dương) trong một dãy tính thường được viết trong dấu ngoặc. Nhờ quy tắc cộng hay trừ số nguyên, ta có thể viết dãy tính dưới dạng không có dấu ngoặc.

Vì phép trừ chuyển được về phép cộng nên các dãy tính như trên cũng được gọi là một tổng.

Ví dụ 1. Tính:

a) (-2) - (-8);

b) 3 + (-9) + (-4) – (-11).

Lời giải

a) (-2) - (-8) = -2 + 8 = 8 – 2 = 6;

b) 3 + (-9) + (-4) – (-11) = 3 – 9 – 4 + 11 = - 6 – 4 + 11 = - 10 + 11 = 1.

Quy tắc dấu ngoặc:

Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữ nguyên dấu của các số hạng trong ngoặc;

Khi bỏ dấu ngoặc có dấu “-” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “+” đổi thành “-” và dấu “-” đổi thành dấu “+”.

Ví dụ 2. Bỏ dấu ngoặc và tính các tổng sau:

a) 232 – (581 + 132 – 331);

b) (56 – 27) – (11 + 28 – 16);

c) [24 + (-37)] – [-37 – (-24)];

d) -321 + (-29) – 142 – (-72).

Lời giải

a) 232 – (581 + 132 – 331)

= 232 – 581 - 132 + 331

= (232 – 132) + (-581 + 331)

= 100 + (-250)

= - (250 – 100)

= - 150.

b) (56 – 27) – (11 + 28 – 16)

= 56 – 27 – 11 – 28 + 16

= 29 – 11 – 28 + 16

= 18 – 28 + 16

= -10 + 16

= 6

c) [24 + (-37)] – [-37 – (-24)]

= 24 + (-37) + 37 – 24

= (24 – 24) + [(-37) + 37]

= 0 + 0

= 0

d) -321 + (-29) – 142 – (-72)

= - 321 + (-29) -142 + 72

= - 250 – 142 + 72

= -392 + 72

= -320

Xem thêm lời giải bài tập Toán lớp 6 sách Kết nối tri thức với cuộc sống hay, chi tiết khác:

Luyện tập chung

Bài 16: Phép nhân số nguyên

Bài 17: Phép chia hết. Ước và bội của một số nguyên

Luyện tập chung

Bài tập cuối Chương 3

Xem thêm tài liệu Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 15: Quy tắc dấu ngoặc

Trắc nghiệm Bài 15: Quy tắc ngoặc