Nội dung bài viết

    Xem thêm

    Giải Toán 11 trang 43 Tập 2 Cánh diều

    Với giải bài tập Toán 11 trang 43 Tập 2 trong Bài 3: Hàm số mũ. Hàm số lôgarit sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 43 Tập 2.

    1 196 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 trang 43 Tập 2

    Hoạt động 4 trang 43 Toán 11 Tập 2: Tìm giá trị y tương ứng với giá trị x trong bảng sau:

    Lời giải:

    Thay x = 1 vào hàm số y = log3x ta được y = log31 = 0.

    Tương tự, thay lần lượt các giá trị x = 1; x = 3; x = 9; x = 27 vào hàm số y = log3x ta được bảng sau:

    x

    1

    3

    9

    27

    y = log3x

    0

    1

    2

    3

    Luyện tập 3 trang 43 Toán 11 Tập 2: Cho hai ví dụ về hàm số lôgarit.

    Lời giải:

    Hai ví về hàm số lôgarit: log3x và log7(x + 2).

    Hoạt động 5 trang 43 Toán 11 Tập 2: Cho hàm số lôgarit y = log2x.

    a) Tìm giá trị y tương ứng với giá trị x trong bảng sau:

    x

    0,5

    1

    2

    4

    8

    y

    ?

    ?

    ?

    ?

    ?

    b) Trong mặt phẳng tọa độ Oxy, biểu diễn điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; log2x) với x ∈ (0; +∞) và nối lại, ta được đồ thị hàm số y = log2x (Hình 6).

    Hoạt động 5 trang 43 Toán 11 Tập 2 | Cánh diều Giải Toán 11

    c)Cho biết tọa độ giao điểm đồ thị hàm số y = log2x với trục hoành và vị trí của đồ thị hàm số đó so với trục tung.

    d)Quan sát đồ thị hàm số y = log2x, nêu nhận xét về:

    • limx→0+log2x,    limx→+∞log2x;

    • Sự biến thiên của hàm số y = log2x và lập bảng biến thiên của hàm số đó.

    Lời giải:

    a) Xét hàm số y = log2x.

    Thay x = 0,5 vào hàm số y = log2x ta được y = log20,5 = y = log22−1 = –1.

    Tương tự, thay lần lượt các giá trị x = 1; x = 2; x = 4; x = 8 vào hàm số y = log2x, ta được bảng sau:

    x

    0,5

    1

    2

    4

    8

    y

    –1

    0

    1

    2

    3

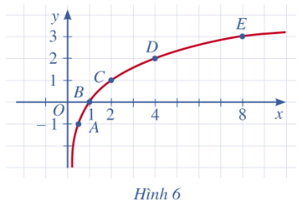
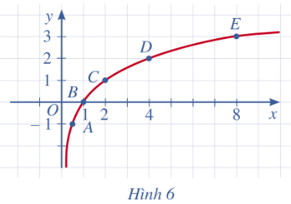
    b) Các điểm A(0,5; –1), B(1; 0), C(2; 1); D(4; 2) và E(8; 3) được biểu diễn trên mặt phẳng tọa độ Oxy như Hình 6.

    Bằng cách làm tương tự, lấy nhiều điểm (x; log2x) với x ∈ (0; +∞) và nối lại, ta được đồ thị hàm số y = log2x (Hình 6).

    Hoạt động 5 trang 43 Toán 11 Tập 2 | Cánh diều Giải Toán 11

    c) Giao điểm đồ thị hàm số y = log2x với trục hoànhlà B(1; 0) và đồ thị hàm số y = log2xnằm ở phía biên phải trục tung, đi lên kể từ trái sang phải.

    d) Từ đồ thị ta thấy:

    • limx→0+log2x=−∞,    limx→+∞log2x=+∞

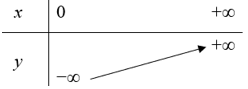
    • Đồ thị hàm số y = log2xđi lên kể từ trái sang phải (với x ∈ (0; +∞)) nên hàm số y = log2xđồng biến trên (0; +∞).

    Bảng biến thiên của hàm số đó:

    Hoạt động 5 trang 43 Toán 11 Tập 2 | Cánh diều Giải Toán 11

    Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

    Giải Toán 11 trang 39 Tập 2

    Giải Toán 11 trang 40 Tập 2

    Giải Toán 11 trang 42 Tập 2

    Giải Toán 11 trang 43 Tập 2

    Giải Toán 11 trang 44 Tập 2

    Giải Toán 11 trang 46 Tập 2

    Giải Toán 11 trang 47 Tập 2

    Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

    Câu hỏi khởi động trang 39 Toán 11 Tập 2: Một doanh nghiệp gửi ngân hàng 1 tỉ đồng với kì hạn 1 năm, lãi suất 6,2%/năm. Giả sử trong suốt n năm (n ∈ ℕ*)...

    Hoạt động 1 trang 39 Toán 11 Tập 2: Xét bài toán ở phần mở đầu. a) Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm;...

    Luyện tập 1 trang 39 Toán 11 Tập 2: Cho hai ví dụ về hàm số mũ...

    Hoạt động 2 trang 39 Toán 11 Tập 2: Cho hàm số mũ y = 2x. a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau...

    Hoạt động 3 trang 40 Toán 11 Tập 2: Cho hàm số mũ y=12x. a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau...

    Luyện tập 2 trang 42 Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số y=13x...

    Hoạt động 4 trang 43 Toán 11 Tập 2: Tìm giá trị y tương ứng với giá trị x trong bảng sau...

    Luyện tập 3 trang 43 Toán 11 Tập 2: Cho hai ví dụ về hàm số lôgarit...

    Hoạt động 5 trang 43 Toán 11 Tập 2: Cho hàm số lôgarit y = log2x. a) Tìm giá trị y tương ứng với giá trị x trong bảng sau...

    Hoạt động 6 trang 44 Toán 11 Tập 2: Cho hàm số lôgarit y=log12x a) Tìm giá trị y tương ứng với giá trị x trong bảng sau...

    Luyện tập 4 trang 46 Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số y=log13x...

    Bài 1 trang 47 Toán 11 Tập 2: Tìm tập xác định của các hàm số: a) y = 12x; b) y = log5(2x – 3); c) y=log15−x2+4 ...

    Bài 2 trang 47 Toán 11 Tập 2: Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao...

    Bài 3 trang 47 Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số: a) y = 4x;b) y=log14x ...

    Bài 4 trang 47 Toán 11 Tập 2: Ta coi năm lấy làm mốc để tính dân số của một vùng (hoặc một quốc gia) là năm 0. Khi đó, dân số của quốc gia đó ở năm thứ t là hàm số theo biến t...

    Bài 5 trang 47 Toán 11 Tập 2: Các nhà tâm lí học sử dụng mô hình hàm số mũ để mô phỏng quá trình học tập của một học sinh như sau: f(t) = c(1 – e–kt)...

    Bài 6 trang 47 Toán 11 Tập 2: Chỉ số hay độ pH của một dung dịch được tính theo công thức: pH = – log[H+]. Phân tích nồng độ ion hydrogen [H+] trong hai mẫu nước sông...

    Bài 7 trang 47 Toán 11 Tập 2: Cô Yên gửi 10 triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất 6% /năm...

    Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

    Bài tập cuối chương 5 trang 25

    Bài 1: Phép tính lũy thừa với số mũ thực

    Bài 2: Phép tính lôgarit

    Bài 4: Phương trình, bất phương trình mũ và lôgarit

    Bài tập cuối chương 6 trang 55

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 196 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: