Giải Toán 11 trang 109 Tập 1 Cánh diều

Với giải bài tập Toán 11 trang 109 trong Bài 4: Hai mặt phẳng song song sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 109.

1 486 02/11/2023

Trang trước

Trang sau

Giải Toán 11 trang 109 Tập 1

Luyện tập 4 trang 109 Toán 11 Tập 1: Bạn Minh cho rằng: Nếu a, b là hai cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì

Phát biểu của bạn Minh có đúng không? Vì sao?

Lời giải:

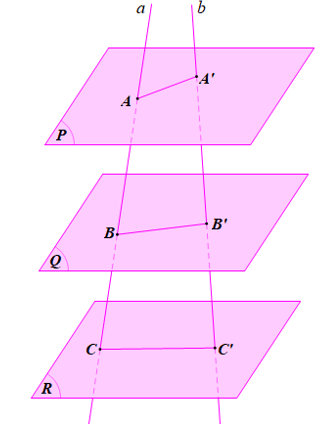
Luyện tập 4 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Theo định lí Thalès, nếu a, b là hai cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì $\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \frac{C A}{C^{'} A^{'}}$ .

Do đó $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}}$ .

Theo bài, bạn Minh phát biểu rằng $\frac{A B}{B C} = \frac{A C}{A^{'} C^{'}}$

Mà do $B C \neq A^{'} B^{'}$ nên phát biểu của bạn Minh là sai.

Bài 1 trang 109 Toán 11 Tập 1: Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?

Lời giải:

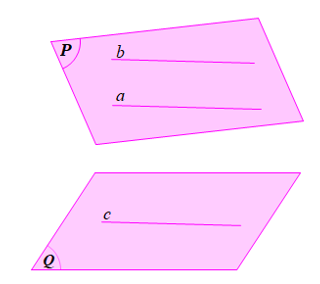
Phát biểu của bạn Chung không đúng vì trong trường hợp này, để (P) // (Q) thì hai đường thẳng a và b trong mặt phẳng (P) cần thêm điều kiện cắt nhau tại một điểm.

Chẳng hạn: xét trường hợp hai đường thẳng a và b song song với nhau trong mp(P) (hình vẽ).

Bài 1 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Do a // (Q) nên tồn tại đường thẳng c nằm trên (Q) sao cho c // a.

Do a // b và c // a nên a // b // c.

Ta có: b // c mà c ⊂ (Q) nên b // (Q).

Trong hình vẽ trên, tuy a // (Q) và b // (Q) nhưng (P) không song song với (Q).

Bài 2 trang 109 Toán 11 Tập 1:Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trong mặt phẳng (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C, D’. Chứng minh rằng A’B’C’D’ là hình bình hành.

Lời giải:

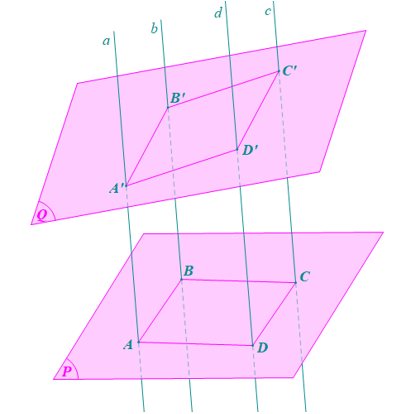
Bài 2 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

• Ta có: AB // CD (do ABCD là hình bình hành).

Mà CD ⊂ mp(CDD’C’) nên AB // (CDD’C’).

Lại có a // d nên A’A // D’D

Mà D’D ⊂ mp(CDD’C’) nên A’A // (CDD’C’).

Ta có: AB // (CDD’C’);

A’A // (CDD’C’);

AB, A’A cắt nhau tại A và cùng nằm trong (ABB’A’)

Do đó (ABB’A’) // (CDD’C’).

Ta có: (ABB’A’) // (CDD’C’);

(ABB’A’) ∩ (Q) = A’B’;

(CDD’C’) ∩ (Q) = C’D’.

Do đó A’B’ // C’D’.

• Tương tự, (ADD’A’) // (BCC’B);

(ADD’A’) ∩ (Q) = A’D’;

(BCC’B) ∩ (Q) = B’C’.

Do đó A’D’ // B’C’.

Tứ giác A’B’C’D’ có A’B’ // C’D’ và A’D’ // B’C’ nên A’B’C’D là hình bình hành.

Bài 3 trang 109 Toán 11 Tập 1: Cho tứ diện ABCD. Lấy G₁, G₂, G₃ lần lượt là trọng tâm của các tam giác ABC, ACD, ADB.

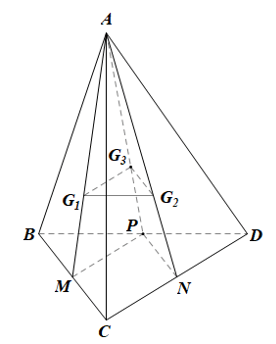
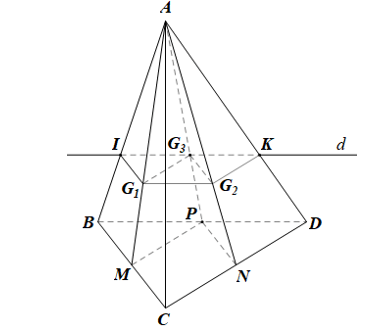
a) Chứng minh rằng (G₁G₂G₃) // (BCD).

b) Xác định giao tuyến của mặt phẳng (G₁G₂G₃) với mặt phẳng (ABD).

Lời giải:

Bài 3 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Gọi M, N, P lần lượt là trung điểm của BC, CD, DB.

Trong mp(ABC), xét $∆$ ABC có G₁ là trọng tâm của tam giác nên $\frac{A G_{1}}{A M} = \frac{2}{3}$ ;

Trong mp(ACD), xét $∆$ ACD có G₂ là trọng tâm của tam giác nên $\frac{A G_{2}}{A N} = \frac{2}{3}$ ;

Trong mp(ABD), xét $∆$ ABD có G₃ là trọng tâm của tam giác nên $\frac{A G_{3}}{A P} = \frac{2}{3}$ .

Trong mp(AMP), xét $∆$ AMP có $\frac{A G_{1}}{A M} = \frac{A G_{3}}{A P} = \frac{2}{3}$ nên G₁G₃ // MP (theo định lí Thalès đảo).

Mà MP ⊂ (BCD) nên G₁G₃ // (BCD).

Chứng minh tương tự ta cũng có $\frac{A G_{2}}{A N} = \frac{A G_{3}}{A P} = \frac{2}{3}$ nên G₂G₃ // NP (theo định lí Thalès đảo).

Mà NP ⊂ (BCD) nên G₂G₃ // (BCD).

Ta có: G₁G₃ // (BCD);

G₂G₃ // (BCD);

G₁G₃, G₂G₃ cắt nhau tại G₃ và cùng nằm trong mp(G₁G₂G₃).

Do đó (G₁G₂G₃) // (BCD).

Bài 3 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Ta có: B, D cùng thuộc hai mặt phẳng (ABD) và (BCD) nên (ABD) ∩ (BCD) = BD.

Giả sử (ABD) ∩ (G₁G₂G₃) = d.

Ta có: (G₁G₂G₃) // (BCD);

(ABD) ∩ (BCD) = BD;

(ABD) ∩ (G₁G₂G₃) = d.

Suy ra d // BD.

Mà G₃ ∈ (ABD) và G₃ ∈ (G₁G₂G₃) nên G₃ là giao điểm của (G₁G₂G₃) và (ABD).

Do đó giao tuyến d của hai mặt phẳng (G₁G₂G₃) và (ABD) đi qua điểm G₃ và song song với BD, cắt AB, AD lần lượt tại I và K.

Vậy (G₁G₂G₃) ∩ (ABD) = IK.

Bài 4 trang 109 Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.

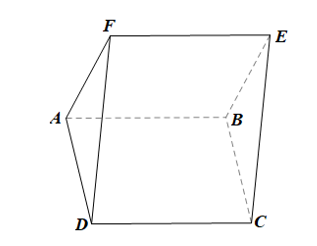
a) Chứng minh rằng (AFD) // (BEC).

b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính $\frac{A N}{N C}$ .

Lời giải:

Bài 4 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Ta có: BE // AF (do ABEF là hình bình hành);

AF ⊂ (AFD)

Do đó BE // (AFD).

Ta cũng có: BC // AD (do ABCD là hình bình hành)

AD ⊂ (AFD)

Do đó BC // (AFD).

Do BE // (AFD);

BC // (AFD);

BE, BC cắt nhau tại điểm B và cùng nằm trong mp(BEC)

Suy ra (AFD) // (BEC).

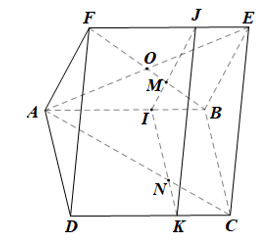
Bài 4 trang 109 Toán 11 Tập 1 | Cánh diều Giải Toán 11

+) Do (AFD) song song với (P) nên tồn tại hai đường thẳng trong (AFD) song song với (P).

• Trong mp(ABEF), qua điểm M vẽ đường thẳng song song với AF, đường thẳng này cắt AB, EF lần lượt tại I, J.

Khi đó IJ // AF, mà AF ⊂ (AFD) nên IJ // (AFD).

• Trong mp(ABCD), qua điểm I vẽ đường thẳng song song với AD, cắt CD tại K.

Khi đó IK // AD, mà AD ⊂ (AFD) nên IK // (AFD).

• Ta có: IJ // (AFD);

IK // (AFD);

IJ, IK cắt nhau tại điểm I và cùng nằm trong mp(IJK).

Do đó (IJK) // (AFD).

Mà M ∈ IJ, IJ ⊂ (IJK) nên mp (P) đi qua M và song song với (AFD) chính là mp(IJK).

+) Trong mp(ABCD), AC cắt IK tại N, khi đó N là giao điểm của AC và (P).

Trong mp(ABCD), xét DABC có IN // BC (do IK // AD // BC) nên theo định lí Thalès ta có: .

Trong mp(ABEF), xét DABF có IM // AF nên theo định lí Thalès ta có: $\frac{A N}{N C} = \frac{A I}{I B}$ .

Gọi O là tâm hình bình hành ABEF. Khi đó O là trung điểm của FB nên FO = OB.

Do M là trọng tâm của $∆$ ABE nên $M B = \frac{2}{3} O B$ và $O M = \frac{1}{3} O B$ .

Ta có: $\frac{A N}{N C} = \frac{A I}{I B} = \frac{F M}{M B} = \frac{F O + O M}{M B} = \frac{O B + \frac{1}{3} O B}{\frac{2}{3} O B} = \frac{\frac{4}{3} O B}{\frac{2}{3} O B} = 2$ .