Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 87 Tập 1 Cánh diều

    Với giải bài tập Toán lớp 10 trang 87 Tập 1 trong Bài 4: Tổng và hiệu của hai vectơ sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 87 Tập 1.

    1 332 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 87 Tập 1

    Bài 1 trang 87 Toán lớp 10 Tập 1: Cho ba điểm M, N, P. Vectơ u→=NP→+MN→ bằng vectơ nào sau đây?

    A. PN→;

    B. PM→;

    C. MP→;

    D. NM→.

    Lời giải:

    u→=NP→+MN→=MN→+NP→=MP→.

    Vậy đáp án đúng là đáp án C.

    Bài 2 trang 87 Toán lớp 10 Tập 1: Cho ba điểm D, E, G. Vectơ v→=DE→+−DG→ bằng vectơ nào sau đây?

    A. EG→;

    B. GE→;

    C. GD→;

    D. ED→.

    Lời giải:

    v→=DE→+−DG→=DE→−DG→=GE→.

    Vậy đáp án đúng là đáp án B.

    Bài 3 trang 87 Toán lớp 10 Tập 1: Cho bốn điểm A, B, C, D. Chứng minh:

    a) AB→+CD→=AD→+CB→;

    b) AB→+CD→+BC→+DA→=0→.

    Lời giải:

    a) Ta có AB→=AD→+DB→ nên AB→+CD→=AD→+DB→+CD→

    AB→+CD→=AD→+CD→+DB→=AD→+CB→.

    Vậy ta có điều phải chứng minh.

    b) AB→+CD→+BC→+DA→=AB→+BC→+CD→+DA→

    AB→+CD→+BC→+DA→=AC→+CA→=AA→=0→.

    Vậy ta có điều phải chứng minh.

    Bài 4 trang 87 Toán lớp 10 Tập 1: Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định sau đúng hay sai?

    a) AB→+AD→=AC→;

    b) AB→+BD→=CB→;

    c) OA→+OB→=OC→+OD→.

    Lời giải:

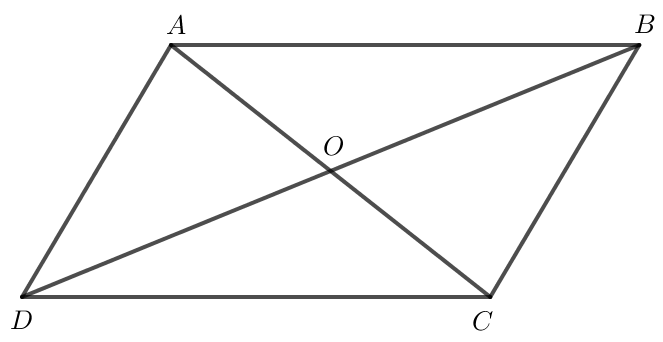
    Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

    a) Do ABCD là hình bình hành nên AD→=BC→.

    Do đó AB→+AD→=AB→+BC→ hay AB→+AD→=AC→.

    Vậy khẳng định a đúng.

    b) Ta có AB→+BD→=AD→.

    Mà AD→=BC→ nên khẳng định b sai.

    c) Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC, OB = OD.

    Mà A và C nằm ở hai phía so với điểm O, B và D nằm ở hai phía so với điểm O nên OA→=−OC→; OB→=−OD→.

    Do đó OA→+OB→=−OC→+OD→.

    Vậy khẳng định c sai.

    Bài 5 trang 87 Toán lớp 10 Tập 1: Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vectơ OA→ và OB→ đối nhau. 

    Lời giải:

    Để hai vectơ OA→ và OB→ đối nhau thì OA = OB và OA→;OB→ ngược hướng nhau.

    Do A và B là hai điểm nằm trên đường tròn nên OA = OB = R.

    Do đó cần thêm điều kiện hai vectơ OA→;OB→ ngược hướng nhau.

    Để hai vectơ OA→;OB→ ngược hướng nhau thì O nằm giữa A và B.

    Mà OA = OB nên O là trung điểm của AB.

    Lại có O là tâm của đường tròn nên AB là đường kính của đường tròn (O).

    Vậy AB là đường kính của đường tròn (O) thì hai vectơ OA→ và OB→ đối nhau.

    Bài 6 trang 87 Toán lớp 10 Tập 1: Cho ABCD là hình bình hành. Chứng minh MB→−MA→=MC→−MD→ với mỗi điểm M trong mặt phẳng.

    Lời giải:

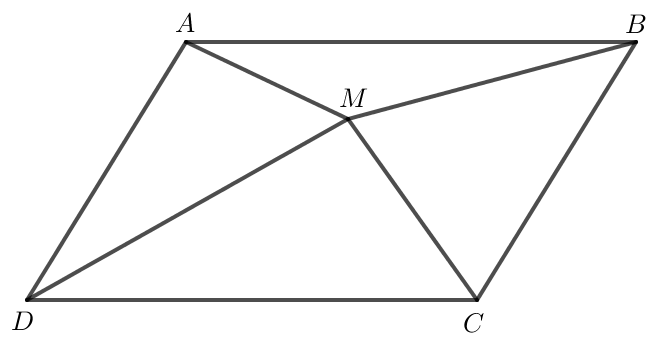
    Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

    Ta có MB→−MA→=AB→; MC→−MD→=DC→.

    Do ABCD là hình bình hành nên AB→=DC→.

    Vậy MB→−MA→=MC→−MD→.

    Bài 7 trang 87 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh a. Tính độ dài của các vectơ sau:

    a) DA→+DC→;

    b) AB→−AD→;

    c) OA→+OB→ với O là giao điểm của AC và BD.

    Lời giải:

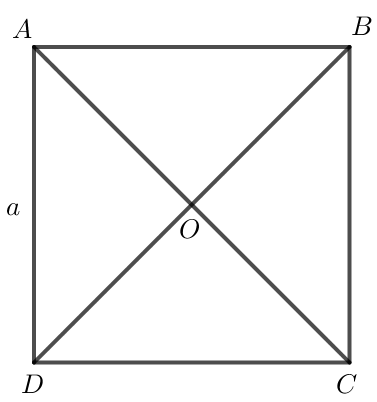
    Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

    a)

     Xét tam giác ABD vuông tại A, có:

    BD2 = AB2 + AD2 (định lí Pythagoras)

    ⇔ BD2 = a2 + a2 = 2a2

    ⇔ BD = a

    Áp dụng quy tắc hình bình hành ta có DA→+DC→=DB→.

    Do đó DA→+DC→=DB→=2a.

    Vậy DA→+DC→=2a.

    b) Ta có AB→−AD→=DB→.

    Do đó AB→−AD→=DB→=2a.

    Vậy AB→−AD→=2a.

    c) Do O là giao điểm hai đường chéo của hình vuông ABCD nên O là trung điểm của AC và BD.

    Do O là trung điểm của BD nên OB→=DO→.

    Do đó OB→+OA→=DO→+OA→=DA→.

    Vậy OB→+OA→=DA→=a .

    Bài 8 trang 87 Toán lớp 10 Tập 1: Cho ba lực F1→=OA→,  F2→=OB→ và F3→=OC→ cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của F1→,  F2→ đều là 120 N và AOB^=120°. Tìm cường độ và hướng của lực F3→.

    Lời giải:

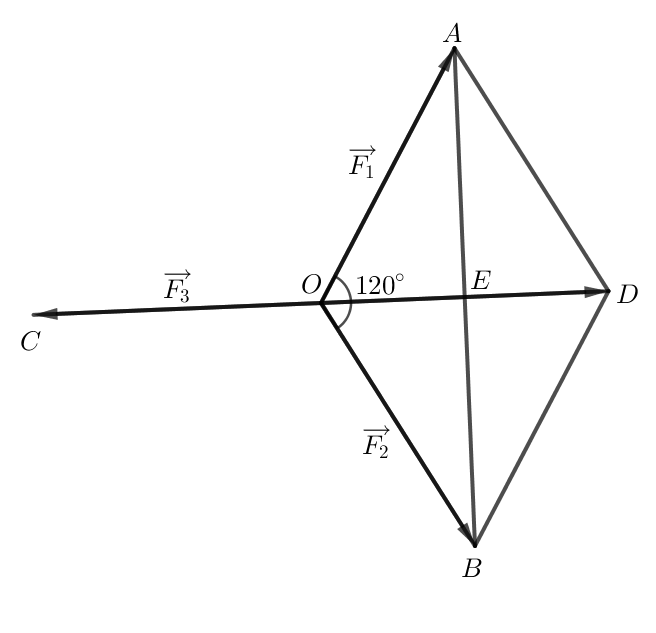
    Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

    Do ba lực Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1) cùng tác động lên vật và vật đứng yên nên Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1).

    ⇒F3→=−F1→+F2→.

    Dựng hình bình hành AOBD.

    Gọi E là giao điểm hai đường chéo AB và OD.

    Áp dụng quy tắc hình bình hành ta có: OA→+OB→=OD→ hay F1→+F2→=OD→.

    ⇒F3→=−OD→.

    Do F1→=F2→ = 120 N nên OA = OB.

    Hình bình hành AOBD có OA = OB nên AOBD là hình thoi.

    Do đó AB⊥OD tại E.

    Do AOBD là hình thoi nên OD là tia phân giác của AOB^.

    Do đó AOE^=12AOB^=12.120°=60°.

    Trong tam giác AOE vuông tại E ta có:

    cosAOE^=OEOA

    ⇒ OE = OA . cos AOE^ = 120 . cos 60o = 60 N.

    Do E là giao điểm hai đường chéo của hình thoi AOBD nên E là trung điểm của OD.

    Do đó OD = 120 N.

    Vậy vectơ F3→ ngược hướng với vectơ OD→ và F3→=−OD→ = 120 N.

    Bài 9 trang 87 Toán lớp 10 Tập 1: Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.

    Lời giải:

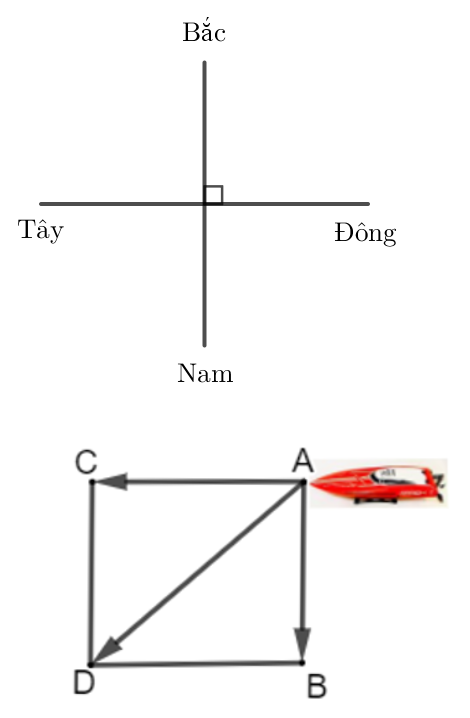
    Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều (ảnh 1)

    Cano chuyển động từ phía đông sang phía tây nên giả sử cano di chuyển từ A sang C, vectơ biểu thị vận tốc so với mặt nước của cano là vectơ AC→.

    Khi đó AC→=40.

    Dòng nước chảy từ phía bắc xuống phía nam nên vectơ biểu thị vận tốc của dòng nước là vectơ AB→.

    Khi đó AB→=10.

    Khi đó vận tốc của cano so với bờ sông được biểu thị bằng vectơ AB→+AC→.

    Dựng hình bình hành ACDB như hình vẽ trên.

    Áp dụng quy tắc hình bình hành ta có:

    AB→+AC→=AD→.

    Do hướng đông tây vuông góc với hướng bắc nam nên AC vuông góc với AB.

    Do đó ACDB là hình chữ nhật.

    Áp dụng định lí Pythagore vào tam giác ABD vuông tại B:

    AD2 = AB2 + BD2

    ⇒ AD2 = 102 + 402

    ⇒ AD2 = 1 700

    ⇒ AD = 1017 km/h

    Vậy vận tốc của cano so với bờ sông bằng 1017 km/h.

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Giải Toán 10 trang 83 Tập 1

    Giải Toán 10 trang 84 Tập 1

    Giải Toán 10 trang 85 Tập 1

    Giải Toán 10 trang 86 Tập 1

    Giải Toán 10 trang 87 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Bài 5: Tích của một số với một vectơ

    Bài 6: Tích vô hướng của hai vectơ

    Bài tập cuối chương 4

    Chủ đề 1: Đo góc

    Bài 1: Mệnh đề toán học

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 332 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: