Nội dung bài viết

    Xem thêm

    Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA

    Lời giải Bài 2 trang 127 SBT Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 1,102 20/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 4: Hai mặt phẳng song song

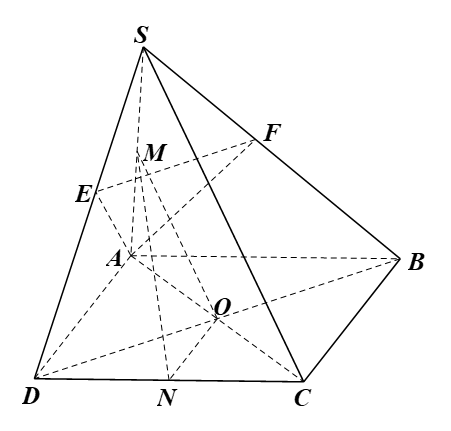
    Bài 2 trang 127 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.

    a) Chứng minh (OMN) // (SBC).

    b) Giả sử hai tam giác SAD và SAB là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác SAD và SAB. Chứng minh EF // (SBD).

    Lời giải:

    Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm

    a) • Xét ∆SAC có: M, O lần lượt là trung điểm của SA, AC nên MO là đường trung bình của tam giác SAC, suy ra MO // SC.

    Mà SC ⊂ (SCB), suy ra MO // (SCB).

    • Xét ∆DCB có: N, O lần lượt là trung điểm của CD, BD nên NO là đường trung bình của tam giác DCB, suy ra NO // BC

    Mà BC ⊂ (SBC), suy ra NO // (SCB).

    Ta có: MO // (SCB);

    NO // (SCB);

    MO, NO ⊂ (OMN); MO ∩ NO = O.

    Vậy (OMN) // (SBC).

    b) Ta có hai tam giác SAD và SAB là các tam giác cân tại A, suy ra AE và AF vừa là

    phân giác vừa là đường trung tuyến lần lượt của hai tam giác SAD và SAB, suy ra E và F lần lượt là trung điểm của SD và SB.

    Suy ra EF là đường trung bình của tam giác SDB nên EF // BD

    Mà BD ⊂ (SBD)

    Suy ra EF // (SBD).

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 127 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC....

    Bài 2 trang 127 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD....

    Bài 3 trang 128 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh: a) (BDA’) // (B’D’C)....

    Bài 4 trang 128 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD....

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

    Bài 2: Hai đường thẳng song song

    Bài 3: Đường thẳng và mặt phẳng song song

    Bài 5: Phép chiếu song song

    Bài tập cuối chương 4 trang 132

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,102 20/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: