Nội dung bài viết

    Xem thêm

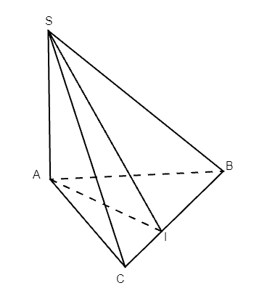
    Cho hình chóp S.ABC có SA vuông góc (ABC). Gọi I là hình chiếu của A trên đường thẳng BC

    Lời giải Bài 26 trang 99 SBT Toán 11 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 325 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

    Bài 26 trang 99 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi I là hình chiếu của A trên đường thẳng BC, α là góc giữa đường thẳng SI và mặt phẳng (ABC), β là số đo nhị diện [S, BC, A]. Phát biểu nào sau đây đúng?

    A. α = 90° – β;

    B. α = 180° – β;

    C. α = 90° + β;

    D. α = β.

    Lời giải:

    Đáp án đúng là: D

    Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi I là hình chiếu của A trên đường thẳng BC

    Do SA ⊥ (ABC) nên hình chiếu của S trên (ABC) là điểm A.

    Suy ra: Góc góc giữa SI và (ABC) chính là SIA^, tức là α=SIA^>. (1)

    Ta có: SA ⊥ (ABC), BC ⊂ (ABC) nên SA ⊥ BC.

    Ta có: BC ⊥ SA, BC ⊥ AI (gt) và AI ∩ SA = A trong (SAI).

    Suy ra: BC ⊥ (SAI) nên SI ⊥ BC (vì SI ⊂ (SAI)).

    Ta thấy: SI ⊥ BC, AI ⊥ BC và SI ∩ AI = I ∈ BC nên SIA^> chính là góc phẳng nhị diện của góc nhị diện [S, BC, A], tức là β=SIA^. (2)

    Từ (1) và (2) ta có: α = β.

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Cánh diều hay, chi tiết khác:

    Bài 24 trang 99 SBT Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau, đường thẳng d cắt (P)...

    Bài 25 trang 99 SBT Toán 11 Tập 2: Cho hai đường thẳng a và b song song với nhau, mặt phẳng (P) cắt a sao cho...

    Bài 26 trang 99 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi I là hình chiếu của A trên đường thẳng BC...

    Bài 27 trang 99 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a...

    Bài 28 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có ABCD là hình vuông, AC cắt BD tại O...

    Bài 29 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD), ABCD là...

    Bài 30 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có AC cắt BD tại O. Gọi α, β lần lượt là số đo...

    Bài 31 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD. Gọi α1, α2, α3, α4 lần lượt là góc giữa các đường thẳng SA, SB, SC, SD...

    Bài 32 trang 100 SBT Toán 11 Tập 2: Một máy nước nóng sử dụng năng lượng mặt trời như ở hình 20 có các ống hấp...

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Cánh diều hay, chi tiết khác:

    Bài 2: Đường thẳng vuông góc với mặt phẳng

    Bài 4: Hai mặt phẳng vuông góc

    Bài 5: Khoảng cách

    Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

    Bài tập cuối chương 8

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 325 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: