Nội dung bài viết

    Xem thêm

    Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự

    Lời giải Bài 4.5 trang 48 SBT Toán 8 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập SBT Toán 8.

    1 525 19/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 15: Định lí Thalès trong tam giác

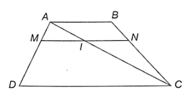
    Bài 4.5 trang 48 SBT Toán 8 Tập 1: Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự tại M, I, N. Chứng minh rằng:

    a) AMMD=BNNC;

    b) AMAD+CNCB=1.

    Lời giải:

    Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC

    a) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: AMMD=AIIC.

    Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: AIIC=BNNC.

    Từ đó, suy ra AMMD=BNNC.

    b) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: AMAD=AIAC.

    Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: CNCB=CICA.

    Khi đó AMAD+CNCB=AIAC+CICA=AI+CICA=ACCA=1.

    Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài 4.1 trang 47 SBT Toán 8 Tập 1: Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:

    a) HK = 3 cm và MN = 9 cm;...

    Bài 4.2 trang 48 SBT Toán 8 Tập 1: Tìm độ dài x trong các hình vẽ sau (H.5.4)...

    Bài 4.3 trang 48 SBT Toán 8 Tập 1: Tìm độ dài x trong Hình 5.5...

    Bài 4.4 trang 48 SBT Toán 8 Tập 1: Cho Hình 5.6. Chứng minh rằng AB // KI...

    Bài 4.5 trang 48 SBT Toán 8 Tập 1: Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự tại M, I, N...

    Bài 4.6 trang 48 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD...

    Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài tập cuối chương 3

    Bài 16: Đường trung bình của tam giác

    Bài 17: Tính chất đường phân giác của tam giác

    Bài tập cuối chương 4

    Bài 18: Thu thập và phân loại dữ liệu

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 525 19/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: