Nội dung bài viết

    Xem thêm

    Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’. Chứng minh AH = A’H

    Lời giải Bài 38 trang 81 SBT Toán 7 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 347 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 Cánh diều Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

    Bài 38 trang 81 SBT Toán 7 Tập 2: Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’. Chứng minh AH = A’H’.

    Lời giải

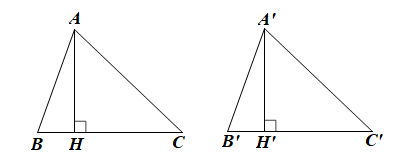
    Sách bài tập Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc  (ảnh 1) 

    Do ∆ABC = ∆A’B’C’ (giả thiết)

    Nên AB = A’B’ (hai cạnh tương ứng) và ABC^=A'B'C'^ (hai góc tương ứng).

    Xét ∆ABH và ∆AB’H’ có:

    AHB^=A'H'B'^=90°,

    AB = A’B’ (chứng minh trên),

    ABH^=A'B'H'^ (do ABC^=A'B'C'^)

    Suy ra ∆ABH = ∆A’B’H’ (cạnh huyền – góc nhọn).

    Do đó AH = A’H’ (hai cạnh tương ứng).

    Vậy AH = A’H’.

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 37 trang 81 SBT Toán 7 Tập 2:Nêu thêm một điều kiện để hai tam giác trong mỗi hình 31a, 31b, 31c, 31d là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc...

    Bài 38 trang 81 SBT Toán 7 Tập 2: Cho ∆ABC = ∆A’B’C’. Vẽ AH vuông góc với BC tại H, A’H’ vuông góc với B’C’ tại H’. Chứng minh AH = A’H’...

    Bài 39 trang 81 SBT Toán 7 Tập 2: Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Vẽ CM vuông góc với AB tại M, BN vuông góc với AC tại N. Chứng minh AM = AN...

    Bài 40 trang 81 SBT Toán 7 Tập 2: Cho Hình 32 có BAC^=90°, AH vuông góc với BC tại H, xAB^=BAH^, Ay là tia đối của tia Ax. BD và CE vuông góc với xy lần lượt tại D và E...

    Bài 41 trang 81 SBT Toán 7 Tập 2: Cho tam giác ABC có ba góc đều nhọn và A^=60°. Tia phân giác của góc ABC cắt AC tại D, tia phân giác của góc ACB cắt AB tại E. BD cắt CE tại I...

    Bài 42* trang 81 SBT Toán 7 Tập 2: Cho tam giác ABC có A^=90°, M là trung điểm của BC. Chứng minh BC = 2AM...

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

    Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

    Bài 7. Tam giác cân

    Bài 8. Đường vuông góc và đường xiên

    Bài 9. Đường trung trực của một đoạn thẳng

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 347 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: