Bài 6 trang 31 Toán 11 Tập 1 | Cánh diều Giải Toán 11
Lời giải Bài 6 trang 31 Toán 11 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 Tập 1.
Giải Toán 11 Bài 3: Hàm số lượng giác và đồ thị
Bài 6 trang 31 Toán 11 Tập 1: Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó t là thời gian tính bằng giây, A là biên độ dao động và x là li độ dao động đều được tính bằng centimét. Khi đó, chu kì T của dao động là T=. Xác định giá trị của li độ khi t = 0, , t = T và vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong trường hợp:
a) A = 3 cm, φ = 0;
b) A = 3 cm, ;
c) A = 3 cm, .
Lời giải:
Từ T = ta có .
Khi đó ta có phương trình li độ là x = Acos.
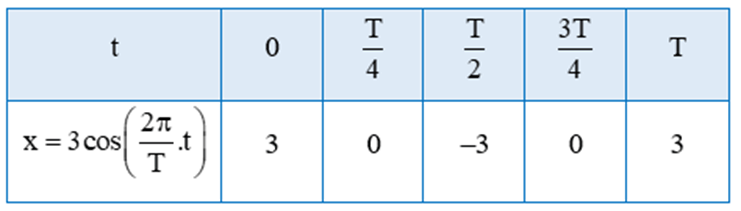
a)
‒ Với A = 3 cm và φ = 0 thay vào phương trình li độ x = Acos ta có:
x = 3cos.
• t = 0 thì x = 3cos0 = 3;
• t = thì x = 3cos= 3cos = 0;
• t = thì x = 3cos = 3cos = -3
• t = thì x = 3cos = 3cos = 0;
• t = T thì x = 3cos = 3cos2 = 3
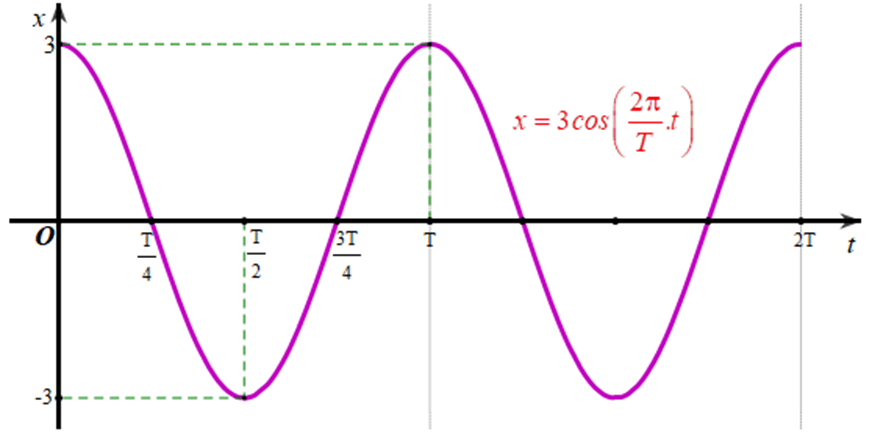
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = 3cos trên đoạn [0; 2T]:
Xét hàm số x = 3cos có chu kì là T.
Ta vẽ đồ thị hàm số x = 3cos trên đoạn [0; T] theo bảng sau:
Bằng cách dịch chuyển đồ thị hàm số x = 3cos trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số x = 3cos trên đoạn [T; 2T].
Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà x = 3cos trên đoạn [0; 2T] như sau:
b)
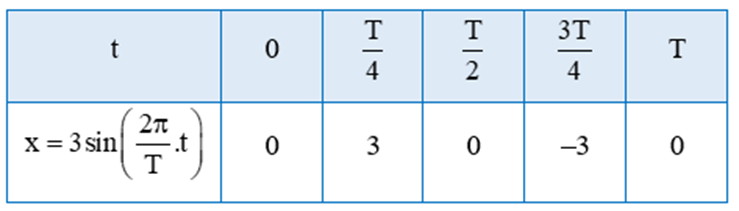
‒ Với A = 3 cm và thay vào phương trình li độ x = Acos ta có:
x = 3cos = 3cos = 3sin
• t = 0 thì x = 3sin = 3sin0 = 0
• t = thì x = 3sin = 3sin = 3;
• t = thì x = 3sin = 3sin = 0;
• t = thì x = 3sin = 3sin = -3;
• t = T thì x = 3sin = 3sin2 = 0.
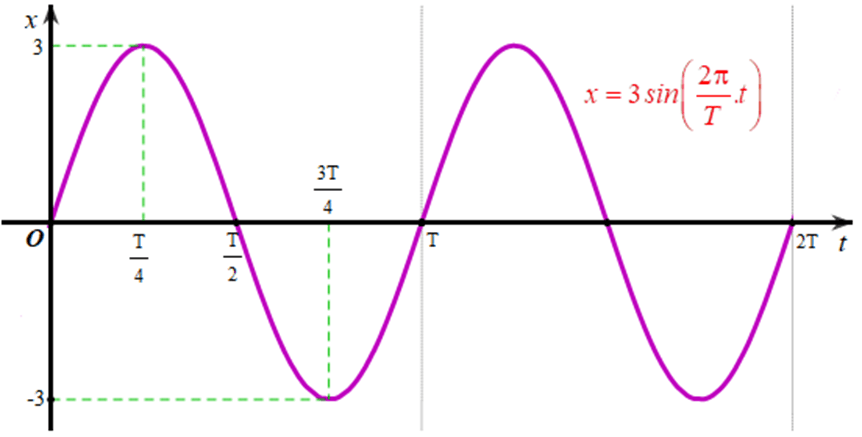
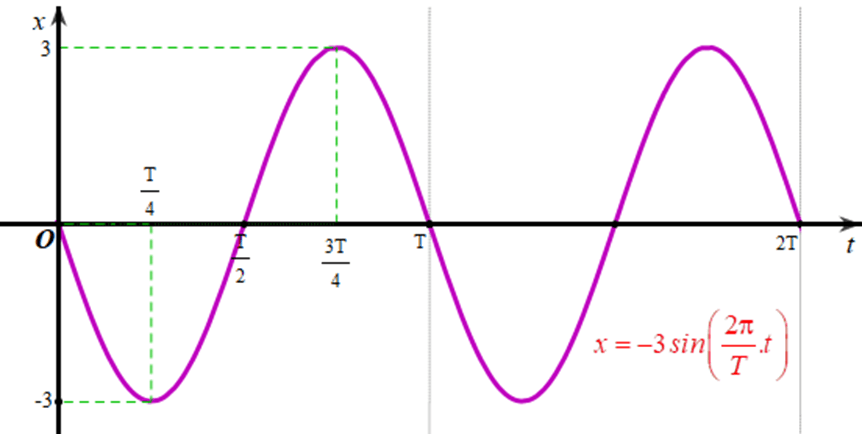
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = 3sin trên đoạn [0; 2T]:
Xét hàm số x = 3sin có chu kì là T.
Ta vẽ đồ thị hàm số x = 3sin trên đoạn [0; T] theo bảng sau:
Bằng cách dịch chuyển đồ thị hàm số x = 3sin trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số x = 3sin trên đoạn [T; 2T].
Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà x = 3sin trên đoạn [0; 2T] như sau:
c)
‒ Với A = 3 cm và thay vào phương trình li độ x = Acos ta có:
x = 3cos = -3cos
= -3cos = -3sin
• t = 0 thì x = -3sin = -3sin0 = 0
• t = thì x = -3sin = -3sin = -3;
• t = thì x = -3sin = -3sin = 0;
• t = thì x = -3sin = -3sin = 3;
• t = T thì x = -3sin = -3sin2 = 0.
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = -3sin trên đoạn [0; 2T]:
Đồ thị hàm số x = -3sin là hình đối xứng với đồ thị hàm số x = 3sin qua trục hoành:
Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 22 Toán 11 Tập 1: a) Cho hàm số f(x) = x2. Với x ∈ ℝ, hãy so sánh f(‒x) và f(x)...
Luyện tập 1 trang 23 Toán 11 Tập 1: a) Chứng tỏ rằng hàm số g(x) = x3 là hàm số lẻ. b) Cho ví dụ về hàm số không là hàm số chẵn và cũng không là hàm số lẻ...
Hoạt động 2 trang 23 Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như Hình 21...
Luyện tập 2 trang 23 Toán 11 Tập 1: Cho ví dụ về hàm số tuần hoàn...
Hoạt động 4 trang 24 Toán 11 Tập 1: Cho hàm số y = sinx. a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau...
Hoạt động 5 trang 25 Toán 11 Tập 1: Quan sát đồ thị hàm số y = sinx ở Hình 24...
Luyện tập 3 trang 25 Toán 11 Tập 1: Hàm số y = sinx đồng biến hay nghịch biến trên khoảng ...
Hoạt động 7 trang 26 Toán 11 Tập 1: Cho hàm số y = cosx. a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau...
Hoạt động 8 trang 27 Toán 11 Tập 1: Quan sát đồ thị hàm số y = cosx ở Hình 27...
Hoạt động 10 trang 28 Toán 11 Tập 1: Cho hàm số y = tanx. a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau...
Hoạt động 11 trang 28 Toán 11 Tập 1: Quan sát đồ thị hàm số y = tanx ở Hình 29...
Hoạt động 13 trang 29 Toán 11 Tập 1: Cho hàm số y = cotx. a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau...
Hoạt động 14 trang 30 Toán 11 Tập 1: Quan sát đồ thị hàm số y = cotx ở Hình 31...
Bài 1 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
a) Hàm số y = sinx nhận giá trị bằng 1;...
Bài 2 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, tìm giá trị của x trên khoảng để:
a) Hàm số y = tanx nhận giá trị bằng ‒1;...
Bài 3 trang 31 Toán 11 Tập 1: Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng: a) y = sinx trên khoảng ;...
Bài 4 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, hãy cho biết: a) Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị sao cho sinα = m;...
Bài 5 trang 31 Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số: a) y = sinx cosx;...
Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Bài 2: Các phép biến đổi lượng giác
Bài 3: Hàm số lượng giác và đồ thị
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều