Bài 5 trang 85 Toán 8 Tập 2 | Cánh diều Giải Toán lớp 8

Giải Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác

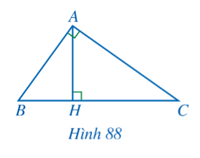
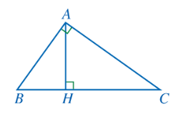
Bài 5 trang 85 Toán 8 Tập 2:Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:

a) ∆ABC ᔕ ∆HBA và AB² = BC.BH;

b) ∆ABC ᔕ ∆HAC và AC² = BC.CH;

c) ∆ABH ᔕ ∆CAH và AH² = BH.CH;

d) $\frac{1}{{\mathrm{AH}}^2}=\frac{1}{{\mathrm{AB}}^2}+\frac{1}{{\mathrm{AC}}^2}.$

Lời giải:

a) Do tam giác ABC vuông tại A, có đường cao AH nên AH ⊥ BC

Do đó $\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHB}}=\widehat{\mathrm{AHC}}=90°$

Xét ∆ABC và ∆HBA có:

$\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHB}}=90°;$ $\hat{A}$ là góc chung

Suy ra ∆ABC ᔕ ∆HBA (g.g).

Do đó $\frac{\mathrm{AB}}{\mathrm{HB}}=\frac{\mathrm{BC}}{\mathrm{BA}}$ (tỉ số đồng dạng)

Nên AB² = BC.BH.

b) Xét ∆ABC và ∆HAC có:

$\widehat{\mathrm{BAC}}=\widehat{\mathrm{AHC}}=90°;$ $\hat{C}$ là góc chung

Suy ra∆ABC ᔕ ∆HAC (g.g).

Do đó $\frac{\mathrm{AC}}{\mathrm{HC}}=\frac{\mathrm{BC}}{\mathrm{AC}}$(tỉ số đồng dạng)

Nên AC² = BC.CH.

c) Do ∆HBA ᔕ ∆ABC (do ∆ABC ᔕ ∆HBA (câu a)) và ∆ABC ᔕ ∆HAC (câu b)

Suy ra ∆HBAᔕ ∆HAC

Hay ∆ABH ᔕ ∆CAH

Suy ra $\frac{\mathrm{AH}}{\mathrm{CH}}=\frac{\mathrm{BH}}{\mathrm{AH}}$(tỉ số đồng dạng)

Nên AH² = BH.CH.

d) Ta có $\frac{1}{{\mathrm{AC}}^2}+\frac{1}{{\mathrm{AB}}^2}=\frac{1}{\mathrm{BC}\cdot \mathrm{CH}}+\frac{1}{\mathrm{BC}\cdot \mathrm{BH}}$

$=\frac{\mathrm{BH}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}+\frac{\mathrm{CH}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}$

$=\frac{\mathrm{BH}+\mathrm{CH}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}=\frac{\mathrm{BC}}{\mathrm{BC}\cdot \mathrm{BH}\cdot \mathrm{CH}}$

$=\frac{1}{\mathrm{BH}\cdot \mathrm{CH}}=\frac{1}{{\mathrm{AH}}^2}.$

Vậy $\frac{1}{{\mathrm{AH}}^2}=\frac{1}{{\mathrm{AB}}^2}+\frac{1}{{\mathrm{AC}}^2}.$