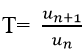Nội dung bài viết

    Xem thêm

    Xét tính tăng, giảm của mỗi dãy số (un), biết: a) un = 2n + 3; b) un = 3^n – n

    Lời giải Bài 11 trang 46 SBT Toán 11 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 3,519 04/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 1: Dãy số

    Bài 11 trang 46 SBT Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số (un), biết:

    a) un = 2n + 3;

    b) un = 3n – n;

    c) un=n2n ;

    d) un = sin n.

    *Phuơng pháp giải:

    a) Ta có un + 1 = 2(n + 1) + 3 = 2n + 5.

    Xét un + 1 – un = (2n + 5) – (2n + 3) = 2 > 0 với mọi n ∈ ℕ*.

    Do đó, un + 1 > un với mọi n ∈ ℕ*.

    Vậy dãy số (un) với un = 2n + 3 là dãy số tăng.

    b) Ta có un + 1 = 3n + 1 – (n + 1) = 3 . 3n – n – 1.

    Xét un + 1 – u­n = (3 . 3n – n – 1) – (3n – n) = 3 . 3n – 3n – 1 = 2 . 3n – 1 > 0 với mọi n ∈ ℕ*.

    Do đó, un + 1 > un với mọi n ∈ ℕ*.

    Vậy dãy số (un) với u­n = 3n – n là dãy số tăng.

    c) Ta có un + 1 = n+12n+1 = n+12.2n .

    Xét un+1−un=n+12.2n−n2n=n+1−2n2.2n =n+1−4n2.2n

    =n+1−4n2.2nn+1+4n=−3n+12.2nn+1+4n<0 với mọi n ∈ ℕ*.

    (do – 3n + 1 < 0, 2n > 0 và với mọi n ∈ ℕ*).

    Do vậy, un + 1 < un với mọi n ∈ ℕ*.

    Vậy dãy số (un) với un=n2n là dãy số giảm.

    *Lý thuyết:

    * Định nghĩa:

    + Dãy số (un) được gọi là dãy số tăng nếu với mọi n ta có un < un + 1

    + Dãy số (un) được gọi là dãy số giảm nếu với mọi n ta có: un > un+1

    * Để xét tính tăng (giảm) của dãy số ta có 2 cách sau:

    + cách 1: Xét hiệu: un+1 − un

    Nếu un+1 − un > 0 thì dãy số tăng.

    Nếu un+1 − un < 0 thì dãy số giảm

    + Cách 2. Nếu các số hạng của dãy un > 0 với mọi n: Xét thương Cách xét tính đơn điệu của dãy số (cực hay có lời giải)

    Nếu T > 1 thì dãy số tăng.

    Nếu T < 1 thì dãy số giảm.

    Xem thêm

    Công thức xét tính đồng biến, nghịch biến hay, chi tiết hay nhất - Toán lớp 9

    TOP 40 câu Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án 2024) - Toán 12

    Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:

    Bài 1 trang 45 SBT Toán 11 Tập 1: Cho dãy số (un) biết u1 = 2 và un=un−1+12  với mọi n ≥ 2. Ba số hạng đầu tiên của dãy số lần lượt là...

    Bài 2 trang 45 SBT Toán 11 Tập 1: Cho dãy số (un) biết un=2n2−1n2+2 . Số hạng u10 là: A. 1912 ...

    Bài 3 trang 45 SBT Toán 11 Tập 1: Cho dãy số (un) biết un=n+13n−2 . Với uk=819  là số hạng của dãy số thì k bằng...

    Bài 4 trang 45 SBT Toán 11 Tập 1: Cho dãy số (un) biết un = 3n. Số hạng un + 1 bằng: A. 3n . 3. B. 3n + 3. C. 3n + 1. D. 3(n + 1)...

    Bài 5 trang 45 SBT Toán 11 Tập 1: Trong các dãy số (un) được xác định như sau, dãy số giảm là: A. un=3n−1n+1 . B. un = n3. C. un=13n+1 . D. un=n ...

    Bài 6 trang 45 SBT Toán 11 Tập 1: Cho dãy số (un) biết un = cos n. Dãy số (un) là: A. Dãy số tăng. B. Dãy số giảm. C. Dãy số bị chặn...

    Bài 7 trang 46 SBT Toán 11 Tập 1: Tính tổng 6 số hạng đầu của dãy số (un), biết un = 3n – 1...

    Bài 8 trang 46 SBT Toán 11 Tập 1: Cho dãy số (un) biết u1 = 2 và un=2+un−12  với mọi n ≥ 2. Viết năm số hạng đầu của dãy số và dự đoán công thức của số hạng tổng quát un...

    Bài 9 trang 46 SBT Toán 11 Tập 1: Trong mặt phẳng toạ độ Oxy, cho hàm số y=2x−12x2+1  có đồ thị (C). Với mỗi số nguyên dương n, gọi An là giao điểm của đồ thị (C) với đường thẳng...

    Bài 10 trang 46 SBT Toán 11 Tập 1: Cho dãy số (un), biết Cho dãy số (un), biết un = sin [(2n-1) π/4] a) Viết bốn số hạng đầu của dãy số...

    Bài 11 trang 46 SBT Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số (un), biết: a) un = 2n + 3; b) un = 3n – n; c) un=n2n ; d) un = sin n...

    Bài 12 trang 46 SBT Toán 11 Tập 1: Cho dãy số (un) biết un=an+2n+1  với a là số thực. Tìm a để dãy số (un) là dãy số tăng...

    Bài 13 trang 46 SBT Toán 11 Tập 1: Chứng minh rằng: a) Dãy số (un) với un=n2+1  bị chặn dưới; b) Dãy số (u­n) với un = – n2 – n bị chặn trên;...

    Bài 14 trang 46 SBT Toán 11 Tập 1: Với mỗi số nguyên dương n, lấy n + 6 điểm cách đều nhau trên đường tròn. Nối mỗi điểm với điểm cách nó hai điểm trên đường tròn đó...

    Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:

    Bài tập cuối chương 1

    Bài 2: Cấp số cộng

    Bài 3: Cấp số nhân

    Bài tập cuối chương 2

    Bài 1: Giới hạn của dãy số

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 3,519 04/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: