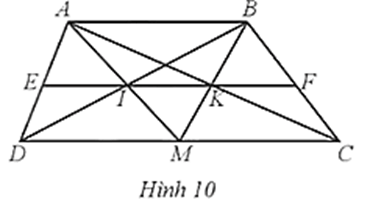
Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm của DC

Lời giải Bài 6 trang 60 SBT Toán 8 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

1 577 30/11/2024

Trang trước

Trang sau

Giải SBT Toán 8 Bài 1: Định lí Thalès trong tam giác

Bài 6 trang 60 SBT Toán 8 Tập 2: Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm của DC; AM cắt BD ở I; BM cắt AC ở K; IK cắt AD, BC lần lượt ở E, F. Chứng minh:

a) IK // AB;

b) EI = IK = KF.

Trong Hình 10, cho biết ABCD là hình thang, AB // CD (AB < CD); M là trung điểm

* Lời giải:

a) Vì M là trung điểm của CD nên DM = MC.

Do AB // CD, M ∈ CD nên AB // DM, AB // CM.

Xét ∆IDM với AB // DM, ta có: $\frac{I A}{I M} = \frac{A B}{D M} = \frac{A B}{M C}$ (do DM = MC) (1)

Xét ∆MKC với AB // CM, ta có: $\frac{K B}{K M} = \frac{A B}{M C}$ (2).

Từ (1) và (2) suy ra $\frac{I A}{I M} = \frac{K B}{K M}$

Xét ∆ABM có $\frac{I A}{I M} = \frac{K B}{K M}$ nên IB // AB (định lí Thalès đảo).

b) Áp dụng định lí Thalès cho ∆ADM với EI // DM, ta có $\frac{E I}{D M} = \frac{A I}{A M}$ (3)

Áp dụng định lí Thales cho ∆AMB với IK // AB, ta có $\frac{A I}{A M} = \frac{B K}{B M}$

Áp dụng định lí Thales cho ∆BMC với KF // MC, ta có $\frac{B K}{B M} = \frac{K F}{M C}$

Do đó, ta có: $\frac{E I}{D M} = \frac{A I}{A M} = \frac{B K}{B M} = \frac{K F}{M C}$ .

Suy ra EI = KF (do DM = MC). (*)

Mặt khác, áp dụng định lí Thalès cho ∆AMC với IK // MC, ta có: $\frac{I K}{M C} = \frac{A I}{A M}$ (4)

Từ (3) và (4) suy ra $\frac{I K}{M C} = \frac{E I}{D M}$ hay IK = EI (do MC = DM). (**)

Từ (*) và (**) suy ra EI = IK = KF

*Phương pháp giải:

Nắm vững lý thuyết và cách dùng định lý Thales trong tam giác để làm bài

* Một số lý thuyết và dạng bài thêm về Định lý Thales trong tam giác:

1. Đoạn thẳng tỉ lệ

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng MN và PQ nếu có tỉ lệ thức: $\frac{A B}{C D} = \frac{M N}{P Q}$

2. Định lí Thalès

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

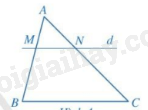
Lý thuyết Định lí Thalès trong tam giác (Cánh diều 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

$\begin{array}{l} Δ A B C, M N / / B C (M \in A B, N \in A C) \\ \Rightarrow \frac{A M}{A B} = \frac{A N}{A C}; \frac{A M}{M B} = \frac{A N}{N C}; \frac{B M}{A B} = \frac{N C}{A C} \end{array}$
3. Định lí Thalès đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Lý thuyết Định lí Thalès trong tam giác (Cánh diều 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

$Δ A B C, M \in A B, N \in A C, \frac{A M}{M B} = \frac{A N}{N C} \Rightarrow M N / / B C$

4. Hệ quả của định lí Thalès

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Lý thuyết Định lí Thalès trong tam giác (Cánh diều 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

$\begin{array}{l} Δ A B C, M N / / B C (M \in A B, N \in A C) \\ \Rightarrow \frac{A M}{A B} = \frac{A N}{A C} = \frac{M N}{B C} \end{array}$