Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 8 Bài 4 (Cánh diều): Tính chất đường phân giác của tam giác

    Với giải sách bài tập Toán 8 Bài 4: Tính chất đường phân giác của tam giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 4.

    1 558 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 4: Tính chất đường phân giác của tam giác

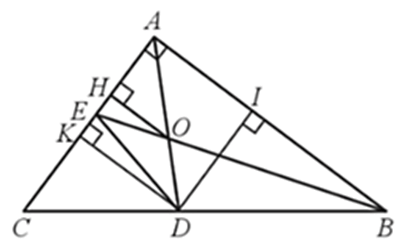
    Bài 21 trang 67 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD, BE cắt nhau tại O. Tính:

    a) Độ dài các đoạn thẳng AE, EC;

    b) Khoảng cách từ O đến đường thẳng AC;

    c) Độ dài đường phân giác AD (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười);

    d) Diện tích tam giác DOE.

    Lời giải:

    Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD

    a) Xét ∆ABC vuông tại A nên theo định lí Pythagore, ta có:

    BC2 = AC2 + AB2 = 62 + 82 = 100, suy ra BC = 10 (cm).

    Xét ∆ABC có BE là phân giác góc ABC nên EAEC=BABC=810=45 (tính chất đường phân giác).

    Suy ra AE4=EC5=AE+EC4+5=AC9=69=23

    Vậy AE=4⋅23=83 (cm); EC=5⋅23=103 (cm).

    b) Kẻ OH ⊥ AC tại H. Khi đó khoảng cách từ O đến đường thẳng AC là độ dài đoạn thẳng OH.

    Ta có OH ⊥ AC, AB ⊥ AC nên OH // AB.

    Xét ∆ABE với OH // AB, ta có: HOAB=EOEB (định lí Thalès) (1).

    Xét ∆AEB có AO là phân giác của góc CAB nên OEOB=AEAB=838=13 (tính chất đường phân giác)

    Suy ra OEOB+OE=13+1 hay EOEB=14 (2).

    Từ (1) và (2) ta có HOAB=14, suy ra OH=14⋅AB=14⋅8=2 (cm).

    c) Kẻ DK ⊥ AC, DI ⊥ AB, suy ra DKA^=DIA^=90°.

    Tứ giác AKDI có DKA^=DIA^=KAI^=90° nên AKDI là hình chữ nhật

    Lại có đường chéo AD là phân giác KAI^ nên AKDI là hình vuông.

    Suy ra AK = DK = DI.

    Ta có S∆ABC = S∆ADC + S∆ADB nên AC⋅AB2=AC⋅DK2+AB⋅DI2

    Hay AC.AB = AC.DK + AB.DI = (AB + AC).DK (do DK = DI).

    Từ đó, ta có: DK=AB⋅ACAB+AC=8⋅68+6=4814=247.

    Xét ∆AKC vuông tại K có AD2 = AK2 + DK2 (định lí Pythagore)

    Suy ra AD2 = AK2 + DK2 = DK2 + DK2 = 2DK2

    Do đó AD=DK2=2427≈4,8 (cm).

    d) Ta có: SΔABC=12AC⋅AB=12⋅6⋅8=24 (cm2).

    Mà SΔBCESΔBAC=12BA⋅EC12BA⋅AC=ECAC=103:6=59

    Do đó SΔBCE=59⋅SΔBAC=59⋅24=403 (cm2).

    Tương tự, ta có: SΔBDESΔBCE=DBCB

    Xét ∆ABC có AD là đường phân giác của góc CAB nên DBDC=ABAC (tính chất đường phân giác)

    Suy ra DBDC+DB=ABAC+AB hay DBCB=88+6=814=47

    Nên SΔBDESΔBCE=DBCB=47.

    Suy ra SΔBDE =47SΔBCE=47⋅403=16021 (cm2)

    Lại có SΔODESΔBDE=OEBE=14

    Suy ra SΔDOE=14⋅SΔBDE=14⋅16021=4021 (cm2).

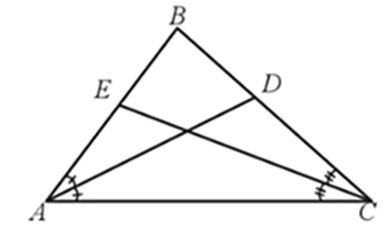
    Bài 22 trang 67 SBT Toán 8 Tập 2: Cho tam giác ABC có chu vi bằng 74 cm. Đường phân giác của góc A chia cạnh BC thành hai đoạn BD và DC tỉ lệ với 2 và 3, đường phân giác của góc C chia cạnh AB thành hai đoạn EB và EA tỉ lệ với 4 và 5. Tính độ dài các cạnh của tam giác ABC.

    Lời giải:

    Cho tam giác ABC có chu vi bằng 74 cm. Đường phân giác của góc A chia cạnh BC

    Trong ∆ABC có:

    AD là phân giác góc A nên ABAC=DBDC=23, suy ra AB2=AC3 hay AB10=AC15 (1)

    CE là phân giác góc C nên CBCA=EBEA=45, suy ra BC4=AC5 hay BC12=AC15 (2)

    Từ (1) và (2) suy ra: AB10=BC12=AC15.

    Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

    AB10=BC12=AC15=AB+BC+AC10+12+15=7437=2.

    Vậy: AB = 2.10 = 20 cm;

    BC = 2.12 = 24 cm;

    AC = 2.15 = 30 cm.

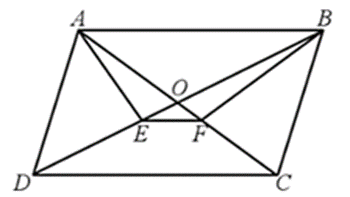
    Bài 23 trang 67 SBT Toán 8 Tập 2: Cho hình bình hành ABCD. Đường phân giác của góc A cắt BD tại E, đường phân giác của góc B cắt AC tại F. Chứng minh:

    a) BEED=AFFC;

    b) EF // AB.

    Lời giải:

    Cho hình bình hành ABCD. Đường phân giác của góc A cắt BD tại E, đường phân giác

    a) Tam giác ABD có AE là đường phân giác của góc A nên EBED=ABAD (1).

    Tam giác ABC có BF là đường phân giác của góc B nên FAFC=BABC (2).

    Vì ABCD là hình bình hành nên AD = BC, do đó ABAD=BABC (3)

    Từ (1) và (2) suy ra EBED=FAFC.

    b) Ta có: EBED=FAFC suy ra EB+EDED=FA+FCFC hay BDED=ACFC

    Gọi O là giao điểm hai đường chéo hình bình hành ABCD. Khi đó O là trung điểm của AC, BD nên BD = 2OD và AC = 2OC.

    Do đó 2ODED=2OCFC hay ODED=OCFC.

    Xét ∆ODC có ODED=OCFC nên EF // CD (định lí Thalès đảo)

    Mà AB // CD (do ABCD là hình bình hành)

    Do đó EF // AB.

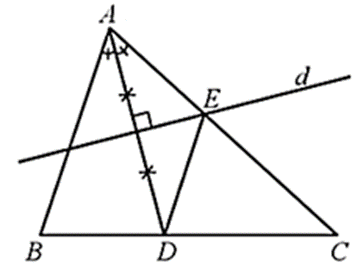
    Bài 24 trang 68 SBT Toán 8 Tập 2: Cho tam giác ABC có đường phân giác AD và AB = 6 cm, AC = 9 cm. Đường trung trực của đoạn AD cắt cạnh AC tại E. Tính độ đài của đoạn thẳng DE.

    Lời giải:

    Cho tam giác ABC có đường phân giác AD và AB = 6 cm, AC = 9 cm

    Ta có E nằm trên đường trung trực của đoạn AD nên EA = ED, do đó tam giác AED cân tại E.

    Suy ra EDA^=EAD^.

    Mà EAD^=DAB^ (do AD là đường phân giác của tam giác ABC)

    Do đó EDA^=DAB^

    Lại có hai góc EDA^, DAB^ở vị trí so le trong nên DE // AB.

    Xét ∆ABC với DE // AB, ta có EDAB=CDCB (hệ quả của định lí Thalès)

    Mặt khác, do AD là đường phân giác của góc BAC nên DCDB=ACAB=96=32

    Nên DCDC+DB=33+2=35

    Suy ra DCBC=35, do đó EDAB=35

    Vậy DE=35AB=35⋅6=3,6 (cm).

    Bài 25 trang 68 SBT Toán 8 Tập 2: Một người đứng ở vị trí M trên cây cầu bắc qua con kênh quan sát ba điểm thẳng hàng A, B, D lần lượt là chân hai cột đèn trồng ở bờ kênh và chân cầu (Hình 26). Người đó nhận thấy góc nhìn đến hai điểm A, D thì bằng góc nhìn đến hai điểm B, D, tức là AMD^=BMD^. Người đó muốn ước lượng tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó. Hỏi có thể ước lượng tỉ số đó được hay không?

    Một người đứng ở vị trí M trên cây cầu bắc qua con kênh quan sát ba điểm thẳng

    Lời giải:

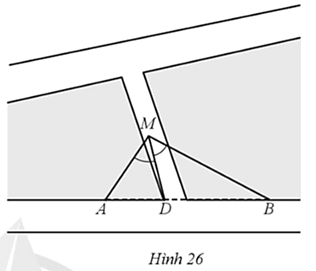
    Ta có AMD^=BMD^ suy ra MD là đường phân giác của góc AMB.

    Do đó MAMB=DADB.

    Vậy người đó có thể ước lượng được tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó bằng cách đo các khoảng cách DA, DB và tính DADB.

    Xem thêm lời giải SBT Toán lớp 8 bộ sách Cánh diều hay, chi tiết khác:

    Bài 5: Tam giác đồng dạng

    Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

    Bài 7: Trường hợp đồng dạng thứ hai của tam giác

    Bài 8: Trường hợp đồng dạng thứ ba của tam giác

    Bài 9: Hình đồng dạng

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 558 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: