Nội dung bài viết

    Xem thêm

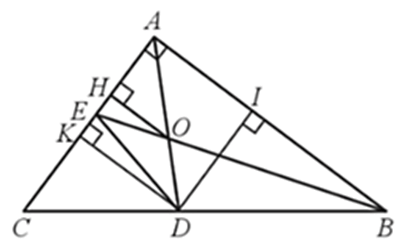
    Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD, BE

    Lời giải Bài 21 trang 67 SBT Toán 8 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

    1 681 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 4: Tính chất đường phân giác của tam giác

    Bài 21 trang 67 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD, BE cắt nhau tại O. Tính:

    a) Độ dài các đoạn thẳng AE, EC;

    b) Khoảng cách từ O đến đường thẳng AC;

    c) Độ dài đường phân giác AD (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười);

    d) Diện tích tam giác DOE.

    Lời giải:

    Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD

    a) Xét ∆ABC vuông tại A nên theo định lí Pythagore, ta có:

    BC2 = AC2 + AB2 = 62 + 82 = 100, suy ra BC = 10 (cm).

    Xét ∆ABC có BE là phân giác góc ABC nên EAEC=BABC=810=45 (tính chất đường phân giác).

    Suy ra AE4=EC5=AE+EC4+5=AC9=69=23

    Vậy AE=4⋅23=83 (cm); EC=5⋅23=103 (cm).

    b) Kẻ OH ⊥ AC tại H. Khi đó khoảng cách từ O đến đường thẳng AC là độ dài đoạn thẳng OH.

    Ta có OH ⊥ AC, AB ⊥ AC nên OH // AB.

    Xét ∆ABE với OH // AB, ta có: HOAB=EOEB (định lí Thalès) (1).

    Xét ∆AEB có AO là phân giác của góc CAB nên OEOB=AEAB=838=13 (tính chất đường phân giác)

    Suy ra OEOB+OE=13+1 hay EOEB=14 (2).

    Từ (1) và (2) ta có HOAB=14, suy ra OH=14⋅AB=14⋅8=2 (cm).

    c) Kẻ DK ⊥ AC, DI ⊥ AB, suy ra DKA^=DIA^=90°.

    Tứ giác AKDI có DKA^=DIA^=KAI^=90° nên AKDI là hình chữ nhật

    Lại có đường chéo AD là phân giác KAI^ nên AKDI là hình vuông.

    Suy ra AK = DK = DI.

    Ta có S∆ABC = S∆ADC + S∆ADB nên AC⋅AB2=AC⋅DK2+AB⋅DI2

    Hay AC.AB = AC.DK + AB.DI = (AB + AC).DK (do DK = DI).

    Từ đó, ta có: DK=AB⋅ACAB+AC=8⋅68+6=4814=247.

    Xét ∆AKC vuông tại K có AD2 = AK2 + DK2 (định lí Pythagore)

    Suy ra AD2 = AK2 + DK2 = DK2 + DK2 = 2DK2

    Do đó AD=DK2=2427≈4,8 (cm).

    d) Ta có: SΔABC=12AC⋅AB=12⋅6⋅8=24 (cm2).

    Mà SΔBCESΔBAC=12BA⋅EC12BA⋅AC=ECAC=103:6=59

    Do đó SΔBCE=59⋅SΔBAC=59⋅24=403 (cm2).

    Tương tự, ta có: SΔBDESΔBCE=DBCB

    Xét ∆ABC có AD là đường phân giác của góc CAB nên DBDC=ABAC (tính chất đường phân giác)

    Suy ra DBDC+DB=ABAC+AB hay DBCB=88+6=814=47

    Nên SΔBDESΔBCE=DBCB=47.

    Suy ra SΔBDE =47SΔBCE=47⋅403=16021 (cm2)

    Lại có SΔODESΔBDE=OEBE=14

    Suy ra SΔDOE=14⋅SΔBDE=14⋅16021=4021 (cm2).

    Xem thêm lời giải SBT Toán lớp 8 bộ sách Cánh diều hay, chi tiết khác:

    Bài 21 trang 67 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, có hai đường phân giác AD...

    Bài 22 trang 67 SBT Toán 8 Tập 2: Cho tam giác ABC có chu vi bằng 74 cm. Đường phân giác của góc A chia cạnh BC...

    Bài 23 trang 67 SBT Toán 8 Tập 2: Cho hình bình hành ABCD. Đường phân giác của góc A cắt BD...

    Bài 24 trang 68 SBT Toán 8 Tập 2: Cho tam giác ABC có đường phân giác AD và AB = 6 cm, AC = 9 cm....

    Bài 25 trang 68 SBT Toán 8 Tập 2: Một người đứng ở vị trí M trên cây cầu bắc qua con kênh quan sát ba điểm thẳng hàng A, B, D...

    Xem thêm lời giải SBT Toán lớp 8 bộ sách Cánh diều hay, chi tiết khác:

    Bài 5: Tam giác đồng dạng

    Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

    Bài 7: Trường hợp đồng dạng thứ hai của tam giác

    Bài 8: Trường hợp đồng dạng thứ ba của tam giác

    Bài 9: Hình đồng dạng

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 681 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: