Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 8 (Cánh diều): Bài tập cuối chương 1

    Với giải sách bài tập Toán 8 Bài tập cuối chương 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8.

    1 1,647 15/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài tập cuối chương 1 - Cánh diều

    Bài 22 trang 17 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử:

    a) 25x2-14;

    b) 36x2 + 12xy + y2;

    c) x32+4;

    d) 27y3 + 27y2 + 9y + 1.

    Lời giải:

    a) 25x2-14=5x2-122=5x-125x+12.

    b) 36x2 + 12xy + y2 = (6x)2 + 2.6.1.xy + y2 = (6x + y)2.

    c) x32+4=12x3+23=12x+2x2-2x+4.

    d) 27y3 + 27y2 + 9y + 1 = (3y)3 + 3.(3y)2.1 + 3.3y.12 + 13 = (3y + 1)3.

    Bài 23 trang 17 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử:

    a) x3(13xy ‒ 5) ‒ y3(5 ‒ 13xy);

    b) 8x3yz + 12x2yz + 6xyz + yz.

    Lời giải:

    a) x3(13xy ‒ 5) ‒ y3(5 ‒ 13xy)

    = x3(13xy ‒ 5) + y3(13xy ‒ 5)

    = (13xy ‒ 5)(x3 + y3)

    = (13xy ‒ 5)(x + y)(x2 ‒ xy + y2).

    b) 8x3yz + 12x2yz + 6xyz + yz

    = yz(8x3 + 12x2 + 6x + 1)

    = yz[(2x)3 + 3.(2x)2.1 + 3.2x.12 + 13)]

    = yx(2x + 1)3.

    Bài 24 trang 18 SBT Toán 8 Tập 1: Tính giá trị của mỗi biểu thức sau:

    a) A=x2+xy+y24 biết x+y2=100.

    b) B = 25x2z ‒ 10xyz + y2zbiết 5x ‒ y = ‒20và z = ‒5.

    c) C = x3yz + 3x2y2z + 3xy3z + y4zbiết x + y = ‒0,5và yz = 8.

    Lời giải:

    a) Ta có: A=x2+xy+y24=x2+2.x.y2+y22=x+y22.

    Thay x+y2=100 vào biểu thức trên ta có: A = 1002 = 10000.

    b) Ta có: B = 25x2z ‒ 10xyz + y2z

    = z(25x2 ‒ 10xy + y2)

    = z[(5x)2 ‒ 2.5x.y + y2)]

    = z(5x ‒ y)2.

    Thay 5x ‒ y = ‒20 và z = ‒5 vào biểu thức trên ta có:

    B = ‒5.(‒20)2 = –5.400 = ‒2 000.

    c) Ta có: C = x3yz + 3x2y2z + 3xy3z + y4z

    = yz(x3 + 3x2y + 3xy2 + y3)

    = yz(x + y)3.

    Thay x + y = ‒0,5 và yz = 8 vào biểu thức trên ta có:

    C=8.-0,53=8.-123=8.-18=-1.

    Bài 25* trang 18 SBT Toán 8 Tập 1: Chứng minh biểu thức B = x5 ‒ 15x2 ‒ x + 5chia hết cho 5 với mọi số nguyên x.

    Lời giải:

    Trước hết, ta chứng minh (x5 ‒ x) ⋮ 5.

    Ta có: x5 ‒ x = x(x4 ‒ 1) = x(x2 ‒ 1)(x2 + 1) = x(x ‒ 1)(x + 1)(x2 + 1)

    • Nếu x = 5k thì x ⋮ 5.

    Khi đó x(x ‒ 1)(x + 1)(x2 + 1) ⋮ 5 hay (x5 ‒ x) ⋮ 5.

    • Nếu x = 5k + 1thì x ‒ 1 = 5k ⋮ 5 .

    Khi đó x(x ‒ 1)(x + 1)(x2 + 1)⋮ 5hay(x5 ‒ x) ⋮ 5.

    • Nếu x = 5k + 2thì x2 + 1 = (5k + 2)2 + 1 = 25k2 + 20k + 5 ⋮ 5.

    Khi đó x(x ‒ 1)(x + 1)(x2 + 1)⋮ 5hay(x5 ‒ x) ⋮ 5.

    • Nếu x = 5k + 3thì x2 + 1 = (5k + 3)2 + 1 = 25k2 + 30k + 10⋮ 5.

    Khi đó x(x ‒ 1)(x + 1)(x2 + 1)⋮ 5hay(x5 ‒ x) ⋮ 5.

    • Nếu x = 5k + 4thì x + 1 = 5k + 5 ⋮ 5.

    Khi đó x(x ‒ 1)(x + 1)(x2 + 1)⋮ 5hay(x5 ‒ x) ⋮ 5.

    Do đó x5 ‒ x ⋮ 5với mọi số nguyên x.

    Ta có: x5 ‒ x ⋮ 5; 15x2⋮ 5; 5 ⋮ 5nên x5 ‒ 15x2 ‒ x + 5⋮ 5với mọi số nguyên x.

    Vậy Bchia hết cho 5 với mọi số nguyên x.

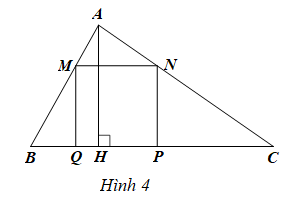
    Bài 26 trang 18 SBT Toán 8 Tập 1: Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0 và hình vuông MNPQ có cạnh MN = y (dm) với y > 0 (Hình 4).

    Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0

    a) Viết công thức tính tổng diện tích của các tam giác AMN, BMQ, CNPdưới dạng tích.

    b) Tính tổng diện tích của các tam giác AMN, BMQ, CNP, biết x ‒ y = 2và x + y = 10.

    Lời giải:

    a) Diện tích của tam giác ABC là:

    12.AH.BC=12.x.2x=x2 (dm2)

    Diện tích hình vuông MNPQ là:

    MN2 = y2 (dm2)

    Vì vậy, tổng diện tích của các tam giác AMN, BMQ, CNP là:

    S = x2 ‒ y2 (dm2)

    b) Từ câu a, ta có

    S = x2 ‒ y2 = (x ‒ y)(x + y)

    Thay x – y = 2 và x + y = 10 vào S ta được:

    S = 2.10 = 20 (dm2).

    Vậy tổng diện tích của các tam giác AMN, BMQ, CNP là20 dm2.

    Bài 27 trang 18 SBT Toán 8 Tập 1: Biểu thức nào sau đây là một đơn thức?

    A. x2 ‒ y.

    B. x2 + y.

    C. x2y.

    D. x2y.

    Lời giải:

    Đáp án đúng là: C

    Biểu thức x2ylà một đơn thức, ta chọn phương án C.

    Bài 28 trang 18 SBT Toán 8 Tập 1: Biểu thức (x ‒ 2y)2 bằng:

    A. x2 + 2xy + 2y2.

    B. x2 ‒ 2xy + 2y2.

    C. x2 + 4xy + 4y2.

    D. x2 ‒ 4xy + 4y2.

    Lời giải:

    Đáp án đúng là: D

    Ta có: (x ‒ 2y)2 = x2 – 2.x.2y + (2y)2 = x2 ‒ 4xy + 4y2.

    Bài 29 trang 18 SBT Toán 8 Tập 1: Biểu thức x3 + 64y3bằng:

    A. (x + 4y)(x2 ‒ 4xy + 16y2).

    B. (x + 4y)(x2 ‒ 4xy + 4y2).

    C. (x + 4y)(x2 + 4xy + 16y2).

    D. (x + 4y)(x2 ‒ 8xy + 16y2).

    Lời giải:

    Đáp án đúng là: A

    Ta có: x3 + 64y3 = x3 + (4y)3

    = (x + 4y)[x2 ‒ x.4y + (4y)2].

    = (x + 4y)(x2 ‒ 4xy + 16y2).

    Bài 30 trang 18 SBT Toán 8 Tập 1: Thực hiện phép tính:

    a) x3-54x2y25x3y4;

    b) -34x5y4xy2-89x2y5.

    Lời giải:

    a) x3-54x2y25x3y4

    =-54.25.x3.x2.x3y.y4

    =-12x8y5.

    b) -34x5y4xy2-89x2y5

    =-34.-89.x5.x.x2y4.y2.y5

    =23x8y11.

    Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

    Bài 1: Phân thức đại số

    Bài 2: Phép cộng, phép trừ phân thức đại số

    Bài 3: Phép nhân, phép chia phân thức đại số

    Bài tập cuối chương 2

    Bài 1: Hàm số

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,647 15/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: