Sách bài tập Toán 8 Bài 7 (Cánh diều): Trường hợp đồng dạng thứ hai của tam giác
Với giải sách bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 7.
Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác
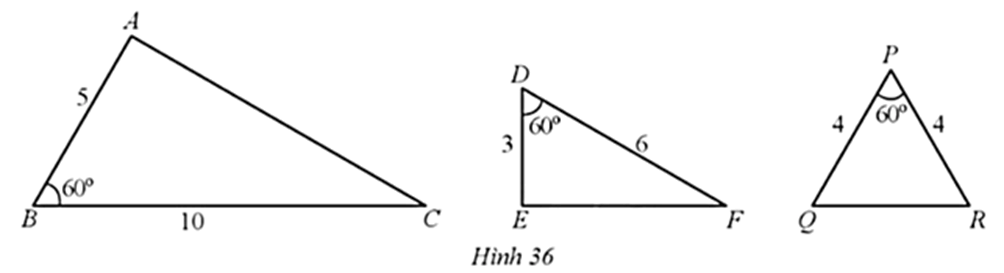
Bài 37 trang 75 SBT Toán 8 Tập 2: Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng:
Lời giải:
Ta có ABDE=53;BCDF=106=53.
Do đó: ABED=BCDF
Xét ∆ABC và ∆EDF có:
ABED=BCDF và ^ABC=^EDF=60°
Suy ra ∆ABC ᔕ ∆EDF (c.g.c).
Lời giải:
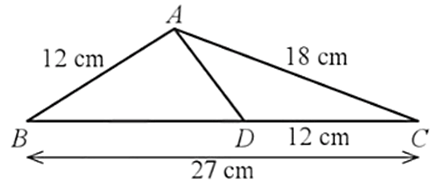
Ta có: ACDC=1812=32; CBCA=2718=32.
Suy ra ACDC=CBCA=32.
Xét ∆ACB và ∆DCA có:
ACDC=CBCA và ^ACB là góc chung
Suy ra ∆ACB ᔕ ∆DCA (c.g.c).
Do đó ACDC=ABDA (tỉ số đồng dạng)
Hay 1812=12AD nên AD=12⋅1218=8 (cm).
Vậy AD = 8 cm.
Lời giải:
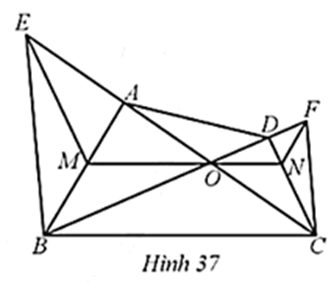
a) Do NF // AB, mà M ∈ AB nên NF // MB.
Xét ∆OBM với NF // MB, ta có OBOF=OMON (hệ quả của định lí Thalès) (1).
Do ME // CD, mà N ∈ CD nên ME // NC.
Xét ∆OEM với ME // NC, ta có OEOC=OMON (hệ quả của định lí Thalès) (2).
Từ (1) và (2) ta có: OBOF=OEOC (=OMON)
Xét ∆OBE và ∆OFC có:
^BOE=^FOC (hai góc đối đỉnh) và OBOF=OEOC (chứng minh trên)
Suy ra ∆OBE ᔕ ∆OFC (c.g.c).
b) Theo câu a, ta có ∆OBE ᔕ ∆OFC nên ^EBO=^OFC (hai góc tương ứng)
Mà hai góc ^EBO và ^OFC ở vị trí so le trong nên suy ra BE // CF.
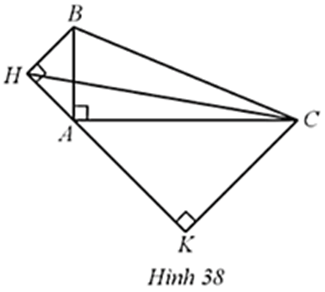
a) Tam giác HAB và tam giác KAC.
b) Tam giác HKC và tam giác BAC.
Lời giải:
a) • Tam giác HAB vuông cân tại H nên HA = HB và HA2 + HB2 = AB2 (định lí Pythagore)
Do đó 2HA2 = AB2 = 52 = 25 hay HA2=HB2=252=(5√2)2
Suy ra HA=HB=5√2 (cm).
• Tam giác KAC vuông cân tại K nên KA = KC và KA2 + KC2 = AC2 (định lí Pythagore)
Do đó 2KA2 = AC2 = 122 = 144 hay KA2=KB2=1442=(12√2)2
Suy ra KA=KC=12√2 (cm).
Ta có: HAKA=5√212√2=512, HBKB=5√212√2=512, nên HAKA=HBKC
Xét ∆HAB và ∆KAC có:
^AHB=^AKC=90° và HAKA=HBKC (chứng minh trên)
Suy ra ∆HAB ᔕ ∆KAC (c.g.c).
b) Ta có: ∆AHB vuông cân tại H nên ^HAB=45°;
∆AKC vuông cân tại K nên ^KAC=45°.
Do đó ^HAK=^HAB+^BAC+^KAC = 45°+90°+45°=180°.
Suy ra ba điểm H, A, K thẳng hàng.
Khi đó HK=AH+AK = 5√2+12√2=17√2 (cm).
⦁ ∆HKC vuông tại K và có hai cạnh góc vuông là: HK=17√2 (cm), KC=12√2 (cm).
∆BAC vuông tại A và có hai cạnh góc vuông là AB = 5 cm, AC = 12 cm.
Ta có: HKAB=17√25=175√2, KCAC=12√212=1√2
Ta thấy HKAB≠KCAC
Do đó tam giác HKC không đồng dạng với tam giác BAC.
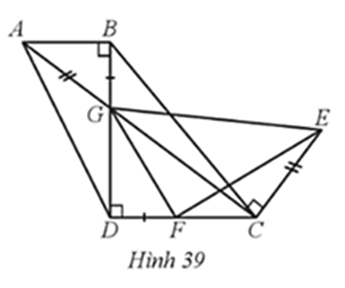
a) ∆FDG ᔕ ∆ECG;
b) ∆GDC ᔕ ∆GFE;
c) ^GFE=90°.
Lời giải:
a) Xét ∆GDC với AB // CD, ta có BGGD=AGGC (hệ quả của định lí Thalès)
Do đó BGAG=GDGC.
Mặt khác AG = CE, BG = DF nên DFCE=GDGC.
Xét ∆FDG và ∆ECG có:
^GDF=^GCE=90° và DFCE=GDGC
Suy ra ∆FDG ᔕ ∆ECG (c.g.c).
b) Vì ∆FDG ᔕ ∆ECG (câu a) nên ^DGF=^CGE (hai góc tương ứng) và DGCG=GFGE (tỉ số đồng dạng)
Từ ^DGF=^CGE ta có ^DGF+^FGC=^CGE+^FGC hay ^DGC=^FGE.
Từ DGCG=GFGE ta có GDGF=GCGE.
Xét ∆GDC và ∆GFE có:
^DGC=^FGE và GDGF=GCGE (chứng minh trên)
Suy ra ∆GDC ᔕ ∆GFE (c.g.c).
c) Vì ∆GDC ᔕ ∆GFE (câu b) nên ^GDC=^GFE (hai góc tương ứng)
Mà ^GDC=90° nên ^GFE=90°.
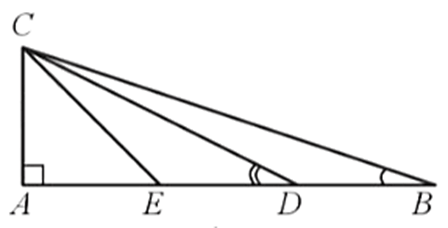
Lời giải:
Gọi E là trung điểm của AD nên AD = 2AE, AE = ED.
Mà AD = 2DB (giả thiết)
Suy ra AE = ED = DB
Do đó AB = AE + ED + BD = 3AE
Mà AB = 3AC (giả thiết) nên AE = AC hay AE = ED = DB = AC.
Đặt AE = x (x > 0).
Suy ra AE = ED = DB = AC = x, EB = 2x.
Xét ∆ACE vuông tại A, theo định lí Pythagore, ta có:
CE2 = AC2 + AE2 = x2 + x2 = 2x2
Suy ra CE=x√2.
Ta có: EDEC=xx√2=1√2, ECEB=x√22x=1√2 nên EDEC=ECEB
Xét ∆EDC và ∆ECB có:
^CEB là góc chung và EDEC=ECEB (chứng minh trên)
Suy ra ∆EDC ᔕ ∆ECB (c.g.c).
Do đó ^ECD=^EBC (hai góc tương ứng)
Vì vậy ^ADC+^ABC=^EDC+^EBC=^EDC+^ECD
Mặt khác, ^AEC là góc ngoài tại đỉnh E của ∆CED nên ^AEC=^EDC+^ECD
Do đó ^ADC+^ABC=^AEC.
Lại có, do ∆AEC là tam giác vuông cân tại A nên ^AEC=45°
Vậy ^ADC+^ABC=45°.
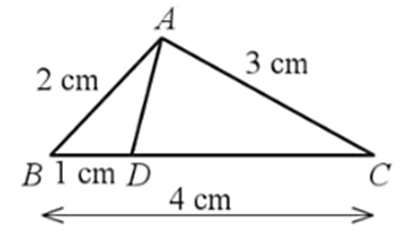
Trên đoạn thẳng BC lấy điểm D sao cho BD = 1 cm.
Suy ra CD = BC ‒ BD = 4 ‒ 1 = 3 cm.
Ta có: BDBA=12; ABCB=24=12nên BDBA=ABCB=12.
Xét ∆ABD và ∆CBA có:
^ABC là góc chung và BDBA=ABCB
Suy ra ∆ABD ᔕ ∆CBA (c.g.c).
Do đó ^BAD=^BCA (hai góc tương ứng) (1).
Tam giác ADC có CD = CA = 3 cm nên là tam giác cân tại C, do đó ^DAC=^ADC (2).
Từ (1) và (2), ta có:
^BAC=^BAD+^DAC=^BCA+^ADC.
Mặt khác, ^ADC là góc ngoài tại đỉnh D của ∆ABD nên ^ADC=^BAD+^ABD.
Do đó ^BAC=^BCA+^BAD+^ABD = ^BCA+^BCA+^ABC=^ABC+2^BCA
Vậy ^BAC=^ABC+2^BCA.
Xem thêm lời giải SBT Toán lớp 8 bộ sách Cánh diều hay, chi tiết khác:
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Cánh diều (hay nhất)
- Văn mẫu lớp 8 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 8 – Cánh diều
- Bố cục tác phẩm Ngữ văn lớp 8 – Cánh diều
- Tác giả tác phẩm Ngữ văn lớp 8 - Cánh diều
- Giải SBT Ngữ văn 8 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Cánh diều
- Soạn văn 8 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 8 – iLearn Smart World
- Giải sbt Tiếng Anh 8 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 8 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 8 ilearn Smart World
- Bài tập Tiếng Anh 8 iLearn Smart World theo Unit có đáp án
- Giải sgk Khoa học tự nhiên 8 – Cánh diều
- Lý thuyết Khoa học tự nhiên 8 – Cánh diều
- Giải sbt Khoa học tự nhiên 8 – Cánh diều
- Giải vbt Khoa học tự nhiên 8 – Cánh diều
- Giải sgk Lịch sử 8 – Cánh diều
- Lý thuyết Lịch sử 8 - Cánh diều
- Giải sbt Lịch sử 8 – Cánh diều
- Giải sgk Địa lí 8 – Cánh diều
- Lý thuyết Địa lí 8 - Cánh diều
- Giải sbt Địa lí 8 – Cánh diều
- Giải sgk Giáo dục công dân 8 – Cánh diều
- Lý thuyết Giáo dục công dân 8 – Cánh diều
- Giải sbt Giáo dục công dân 8 – Cánh diều
- Giải sgk Công nghệ 8 – Cánh diều
- Lý thuyết Công nghệ 8 - Cánh diều
- Giải sbt Công nghệ 8 – Cánh diều
- Giải sgk Tin học 8 – Cánh diều
- Lý thuyết Tin học 8 - Cánh diều
- Giải sbt Tin học 8 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 8 – Cánh diều