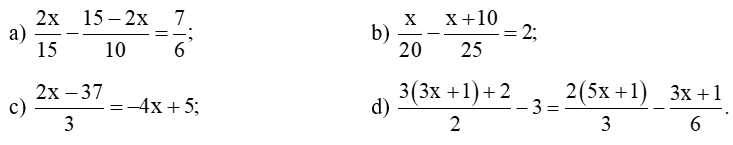Sách bài tập Toán 8 Bài 1 (Cánh diều): Phương trình bậc nhất một ẩn

Giải SBT Toán 8 Bài 1: Phương trình bậc nhất một ẩn

Bài 1 trang 41 SBT Toán 8 Tập 2: Kiểm tra xem số nào là nghiệm của phương trình tương ứng sau đây.

a) 6,36 ‒ 5,3x = 0 với x = ‒1,5; x = 1,2.

b) $-\frac{5}{9}x+1=\frac{2}{3}x-10$ với x = 6; x = 9.

c) 11 ‒ 2x = x ‒ 1 với x = ‒ 4; x = 4.

d) 3x + 1 = 7x ‒ 11 với x = ‒2; x = 3.

Lời giải:

a) • Với x = ‒1,5 tính giá trị vế trái ta có:

6,36 ‒ 5,3x = 6,36 ‒ 5,3.(‒1,5) = 14,31 ≠ 0.

Với x = ‒1,5 giá trị của vế trái khác giá trị của vế phải.

Do đó, x = ‒1,5 không là nghiệm của phương trình 6,36 ‒ 5,3x = 0.

• Với x = 1,2 tính giá trị vế trái ta có:

6,36 ‒ 5,3x = 6,36 ‒ 5,3.1,2 = 0.

Do đó, x = 1,2 là nghiệm của phương trình 6,36 ‒ 5,3x = 0.

b) • Với x = 6, tính giá trị mỗi vế của phương trình ta có:

$-\frac{5}{9}x+1$ = $-\frac{5}{9}\cdot 6+1$ = $-\frac{27}{9}$ = -3; $\frac{2}{3}x-10$ = $\frac{2}{3}\cdot 6-10$ = -6.

Với x = 6 giá trị của vế trái khác giá trị của vế phải.

Do đó, x = 6 không là nghiệm của phương trình $-\frac{5}{9}x+1=\frac{2}{3}x-10$.

• Với x = 9, tính giá trị mỗi vế của phương trình ta có:

$-\frac{5}{9}x+1$ = $-\frac{5}{9}\cdot 9+1$ = -4; $\frac{2}{3}x-10$ = $\frac{2}{3}\cdot 9-10$ = -4.

Do đó, x = 9 là nghiệm của phương trình $-\frac{5}{9}x+1=\frac{2}{3}x-10$.

c) • Với x = ‒4, tính giá trị mỗi vế của phương trình ta có:

11 ‒ 2x = 11 ‒ 2.(‒4) = 19; x ‒ 1 = (‒4) ‒ 1 = ‒5.

Với x = ‒4 giá trị của vế trái khác giá trị của vế phải.

Do đó, x = ‒4 không là nghiệm của phương trình 11 ‒ 2x = x ‒ 1.

• Với x = 4, tính giá trị mỗi vế của phương trình ta có:

11 ‒ 2x = 11 ‒ 2.4 = 3; x ‒ 1 = 4 ‒ 1 = 3.

Do đó, x = 4 là nghiệm của phương trình 11 ‒ 2x = x ‒ 1.

d) • Với x = ‒2, tính giá trị mỗi vế của phương trình ta có:

3x + 1 = 3.(‒2) + 1 = ‒5; 7x ‒ 11 = 7.(‒2) ‒ 11 = ‒25.

Với x = ‒2 giá trị của vế trái khác giá trị của vế phải.

Do đó, x = ‒2 không là nghiệm của phương trình 3x + 1 = 7x ‒ 11.

• Với x = 3, tính giá trị mỗi vế của phương trình ta có:

3x + 1 = 3.3 + 1 = 10; 7x ‒ 11 = 7.3 ‒ 11 = 10.

Do đó, x = 3 là nghiệm của phương trình 3x + 1 = 7x ‒ 11.

Bài 2 trang 41 SBT Toán 8 Tập 2: Tìm giá trị của t để mỗi phương trình có nghiệm tương ứng:

a) 3x + t = 0 có nghiệm x = ‒2;

b) 7x ‒ t = 0 có nghiệm x = ‒1;

e) $\frac{1}{3}x$ + t = 0 có nghiệm x = $\frac{1}{2}$.

Lời giải:

a) Do phương trình 3x + t = 0 có nghiệm x = ‒2 nên thay x = ‒2 vào phương trình 3x + t = 0, ta được:

3.(‒2) + t = 0

−6 + t = 0

t = 6.

Vậy để phương trình đã cho có nghiệm x = ‒2 thì t = 6.

b) Do phương trình 7x ‒ t = 0 có nghiệm x = ‒1 nên thay x = ‒1 vào phương trình 7x ‒ t = 0, ta được:

7.(‒1) ‒ t = 0

‒7 – t = 0

t = ‒7.

Vậy để phương trình đã cho có nghiệm x = ‒1 thì t = ‒7.

c) Do phương trình $\frac{1}{3}x$ + t = 0 có nghiệm x = $\frac{1}{2}$ nên thay x = $\frac{1}{2}$ vào phương trình $\frac{1}{3}x$ + t = 0, ta được:

$\frac{1}{3}\cdot \frac{1}{2}$ + t = 0

$\frac{1}{6}$ + t = 0

t = $-\frac{1}{6}$.

Vậy để phương trình đã cho có nghiệm x = $\frac{1}{2}$ thì t = $-\frac{1}{6}$.

Bài 3 trang 42 SBT Toán 8 Tập 2: Cho hai phương trình ẩn x:

3(x ‒ k) + k + 1 = 0 (1)

5x = 4(2x ‒ k) (2)

a) Xác định giá trị của k, biết phương trình (1) nhận x = 5 làm nghiệm.

b) Giải phương trình (2) với giá trị của k tìm được ở câu a.

Lời giải:

a) Do phương trình (1) nhận x = 5 làm nghiệm nên thay x = 5 vào phương trình (1) ta có:

3(5 ‒ k) + k + 1

15 ‒ 3k + k + 1 = 0

‒ 3k + k = ‒ 1 – 15

‒2k = ‒ 16

k = ‒16 : (‒2)

k = 8.

Vậy để phương trình 3(x ‒ k) + k + 1 = 0 nhận x = 5 làm nghiệm thì k = 8.

b) Với k = 8 phương trình (2) trở thành: 5x = 4(2x ‒ 8).

Giải phương trình:

5x = 4(2x ‒ 8)

5x = 8x ‒ 32

5x – 8x = – 32

–3x = –32

x = (–32) : (–3)

x = $\frac{32}{3}$.

Vậy với k = 8, phương trình (2) có nghiệm là x = $\frac{32}{3}$.

Bài 4 trang 42 SBT Toán 8 Tập 2: Giải các phương trình:

a) 11x + 197 = 0;

b) $\frac{17}{4}$x - 5 = 0;

c) ‒3x ‒ 1 = 3;

d) 11 ‒ 6x = ‒x + 2;

e) 3,4(x + 2) ‒ 2x = 5,5;

f) 5x + 7 = 2(x ‒ 1).

Lời giải:

a) 11x + 197 = 0

11x = ‒ 197

x = $-\frac{197}{11}$

Vậy phương trình có nghiệm x = $-\frac{197}{11}$.

b) $\frac{17}{4}x$ - 5 = 0

$\frac{17}{4}x$ = 5

x = $\frac{20}{17}$

Vậy phương trình có nghiệm x = $\frac{20}{17}$.

c) ‒3x ‒ 1 = 3

‒3x = 3 + 1

‒3x = 4

x = $\frac{-4}{3}$

Vậy phương trình có nghiệm x = $\frac{-4}{3}$.

d) 11 ‒ 6x = ‒x + 2

‒6x + x = 2 ‒ 11

‒5x = ‒9

x = $\frac{9}{5}$

Vậy phương trình có nghiệm x = $\frac{9}{5}$.

e) 3,4(x + 2) ‒ 2x = 5,5

3,4x + 6,8 ‒ 2x = 5,5

3,4x ‒ 2x = 5,5 ‒ 6,8

1,4x = ‒ 1,3

x = $-\frac{13}{14}$

Vậy phương trình có nghiệm x = $-\frac{13}{14}$.

f) 5x + 7 = 2(x ‒ 1)

5x + 7 = 2x ‒ 2

5x ‒ 2x = ‒2 ‒ 7

3x = ‒9

x = ‒3.

Vậy phương trình có nghiệm x = ‒3.

Bài 5 trang 42 SBT Toán 8 Tập 2: Giải các phương trình:

Lời giải:

a) $\frac{2x}{15}-\frac{15-2x}{10}=\frac{7}{6}$

$\frac{2\cdot 2x}{30}-\frac{3\left(15-2x\right)}{30}=\frac{7\cdot 5}{30}$

4x ‒ 45 + 6x = 35

4x + 6x = 35 + 45

10x = 80

x = 8.

Vậy phương trình có nghiệm x = 8.

b) $\frac{x}{20}-\frac{x+10}{25}=2$

$\frac{5\cdot x}{100}-\frac{4\cdot \left(x+10\right)}{100}=\frac{2\cdot 100}{100}$

5x ‒ 4x ‒ 40 = 200

5x ‒ 4x = 200 + 40

x = 240.

Vậy phương trình có nghiệm x = 240.

c) $\frac{2x-37}{3}$ = -4x + 5

$\frac{2x-37}{3}=\frac{3\cdot \left(-4x+5\right)}{3}$

2x ‒ 37 = ‒12x + 15

2x + 12x = 15 + 37

14x = 52

x = $\frac{26}{7}$.

Vậy phương trình có nghiệm x = $\frac{26}{7}$.

d) $\frac{3\left(3x+1\right)+2}{2}-3=\frac{2\left(5x+1\right)}{3}-\frac{3x+1}{6}$

$\frac{3\cdot \left(9x+3+2\right)}{6}-\frac{3\cdot 6}{6}=\frac{2\cdot \left(10x+2\right)}{6}-\frac{3x+1}{6}$

3(9x + 5) ‒ 18 = 2(10x + 2) ‒ 3x ‒ 1

27x + 15 ‒ 18 = 20x + 4 ‒ 3x ‒ 1

27x ‒ 20x + 3x = 4 ‒ 1 ‒ 15 + 18

10x = 6

x = 0,6.

Vậy phương trình có nghiệm x = 0,6.

Bài 6 trang 42 SBT Toán 8 Tập 2: Cho hai phương trình:

3(x ‒ 1) = 2x (1)

|x – 1| = 2 (2)

a) Chứng tỏ hai phương trình có nghiệm chung x = 3.

b) Chứng tỏ x = ‒1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1).

Lời giải:

a) ⦁ Thay x = 3 vào 2 vế của phương trình (1) ta có:

3(x ‒ 1) = 3(3 ‒ 1) = 3.2 = 6; 2x = 2.3 = 6.

Do đó, x = 3 là nghiệm của phương trình (1).

⦁ Thay x = 3 vào vế trái của phương trình (2) ta có:

|x – 1| = |3 – 1| = |2| = 2.

Do đó, x = 3 là nghiệm của phương trình (2).

Vậy x = 3 là nghiệm chung của hai phương trình.

b) ⦁ Thay x = ‒1 vào 2 vế của phương trình (1) ta có

3(x ‒ 1) = 3(‒1 ‒ 1) = 3.(‒2) = ‒6; 2x = 2.(‒1) = ‒2.

Ta thấy giá trị của vế trái khác vế phải.

Do đó x = ‒1 không là nghiệm của phương trình (1).

⦁ Thay x = ‒1 vào phương trình (2) ta có:

|x – 1| = |–1 – 1| = |–2| = 2.

Nên x = ‒1 là nghiệm của phương trình (2).

Vậy x = ‒1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1).

Bài 7 trang 42 SBT Toán 8 Tập 2: Cho A = $\frac{3x-1}{4}$; B = $\frac{7-4x}{5}$. Tìm giá trị của x để:

a) A = B;

b) A ‒ B = 2.

Lời giải:

a) Để A = B thì:

$\frac{3x-1}{4}=\frac{7-4x}{5}$

$\frac{5\left(3x-1\right)}{20}=\frac{4\left(7-4x\right)}{20}$

15x ‒ 5 = 28 ‒ 16x

15x + 16x = 28 + 5

31x = 33

x = $\frac{33}{31}$

Vậy x = $\frac{33}{31}$ thì A = B.

b) Để A ‒ B = 2 thì:

$\frac{3x-1}{4}-\frac{7-4x}{5}$ = 2

$\frac{5\left(3x-1\right)}{20}-\frac{4\left(7-4x\right)}{20}=\frac{2\cdot 20}{20}$

15x ‒ 5 ‒ 28 + 16x = 40

15x + 16x = 40 + 5 + 28

31x = 73

x = $\frac{73}{31}$

Vậy x = $\frac{73}{31}$ thì A ‒ B = 2.

Bài 8 trang 42 SBT Toán 8 Tập 2: Người ta dùng một đoạn dây thép và uốn nó thành hai hình vuông ABCD, MNPQ như Hình 2. Độ dài cạnh hình vuông MNPQ là x (cm). Độ dài cạnh hình vuông ABCD hơn ba lần độ dài cạnh hình vuông MNPQ là 3 cm. Sau khi uốn xong còn thừa đoạn dây thép ME dài 2 cm. Tìm x, biết độ dài đoạn dây thép đã dùng là 62 cm.

Lời giải:

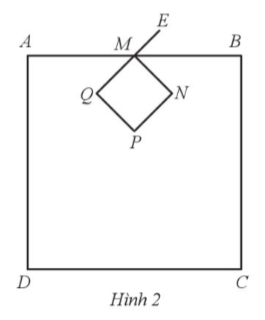
Độ dài cạnh hình vuông MNPQ là x (cm).

Độ dài dây thép cần dùng để uốn thành hình vuông MNPQ là: 4x (cm).

Độ dài cạnh hình vuông ABCD là: 3x + 3 (cm).

Độ dài dây thép cần dùng để uốn thành hình vuông ABCD là: 4(3x + 3) (cm).

Do sau khi uốn xong còn thừa đoạn dây thép ME dài 2 cm và tổng độ dài đoạn dây thép đã dùng là 62 cm nên ta có phương trình:

4x + 4(3x + 3) + 2 = 62

4x + 12x + 12 + 2 = 62

16x = 62 ‒ 12 ‒ 2

16x = 48

x = 3

Vậy x = 3.

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 4: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Bài 5: Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Bài tập cuối chương 6 trang 30

Bài 2: Ứng dụng của phương trình bậc nhất một ẩn

Bài tập cuối chương 7 trang 49