Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác

    Với giải sách bài tập Toán 8 Bài 2: Tứ giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 2.

    1 1,313 15/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 2: Tứ giác

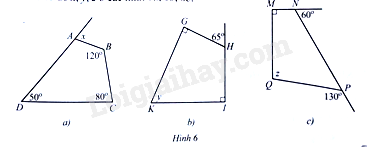
    Bài 6 trang 89 SBT Toán 8 Tập 1: Tính các số đo x,y,z ở các hình 6a,6b,6c:

     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 1)

    Lời giải:

    a)  Trong tứ giác ABCD, ta có: DAB^+B^+C^+D^=360∘.

    Do đó: DAB^=360∘−(B^+C^+D^)=360∘−(120∘+80∘+50∘)=110∘

    Ta có: DAB^+x=180∘ (hai góc kề bù)

    Suy ra x=180∘−110∘=70∘

    b) Ta có: GHI^+65∘=180∘ (hai góc kề bù). Suy ra GHI^=115∘

    Trong tứ giác GHIK, ta có: G^+GHI^+I^+K^=360∘

    Do đó: 90∘+115∘+90∘+y=360∘ hay y+295∘=360∘. Suy ra y=65∘

    c) Ta có: MNP^+60∘=180∘ (hai góc kề bù). Suy ra MNP^=120∘

    Ta lại có: NPQ^+130∘=180∘ (hai góc kề bù). Suy ra NPQ^=50∘

    Trong tứ giác MNPQ, ta có: M^+MNP^+NPQ^+Q^=360∘

    Do đó 90∘+120∘+50∘+z=360∘ hay z+260∘=360∘. Suy ra z=100∘.

    Bài 7 trang 90 SBT Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác ABCD ở Hình 7 (tại mỗi đỉnh chỉ nhọn một góc ngoài):

    A1^+B1^+C1^+D1^=360∘.

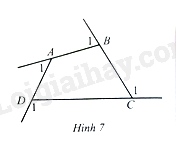
     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 2)

    Lời giải:

    Trong tứ giác ABCD, ta có: DAB^+ABC^+BCD^+CDA^=360∘

    Ta có: DAB^+A1^=ABC^+B1^=BCD^+C1^=CDA^+D1^=180∘ (các cặp góc kề bù)

    Suy ra (180∘−A1^)+(180∘−B1^)+(180∘−C1^)+(180∘−D1^)=360∘

    Hay 720∘−(A1^+B1^+C1^+D1^)=360∘. Vậy A1^+B1^+C1^+D1^=360∘.

    Bài 8 trang 90 SBT Toán 8 Tập 1: a) Cho tứ giác ABCD có AB//CD,B^=135∘,D^=70∘,ACB^=25∘ (Hình 8a). Tính số đo góc DAC.

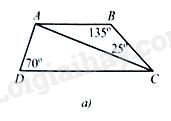
     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 3)

    b) Cho tứ giác GHIK có KGH^=K^=90∘,I^=65∘. Trên HI lấy điểm E sao cho EGH^=25∘ (Hình 8b). Tính số đo góc GEI.

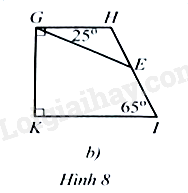
     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 4)

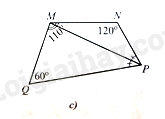
    c) Cho tứ giác MNPQ có PM là tia phân giác của góc NPQ,QMN^=110∘,N^=120∘,Q^=60∘ (Hình 8c). Tính các số đo góc NPM,MPQ,QMP.

     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 5)

    Lời giải:

    a)  Trong tam giác ABC, ta có: BAC^=180∘−(B^+BCA^)=20∘

    Do AB//CD nên ACD^=BAC^=20∘ (hai góc so le trong)

    Trong tam giác ACD, ta có: DAC^=180∘−(ACD^+D^)=90∘

    b) Trong tứ giác GHIK, ta có: H^=360∘−(KGH^+I^+K^)=115∘

    Trong tam giác GHE, ta có: HEG^=180∘−(EGH^+H^)=40∘

    Vậy GEI^=180∘−HEG^=140∘

    c) Trong tứ giác MNPQ, ta có: NPQ^=360∘−(QMN^+N^+Q^)=70∘

    Do PM là tia phân giác của góc NPQ nên NPM^=MPQ^=NPQ^2=35∘

    Trong tam giác MPQ, ta có: QMP^=180∘−(MPQ^+Q^)=85∘

    Bài 9 trang 90 SBT Toán 8 Tập 1: Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

    Lời giải:

    Gọi O là giao điểm của hai đường chéo AC và BD trong tứ giác ABCD.

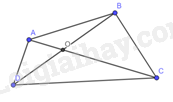
     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 6)

    Xét tam giác OAB, ta có: OA+OB>AB

    Xét tam giác OCD, ta có: OC+OD>CD

    Suy ra OA+OB+OC+OD>AB+CD

    Hay AC+BD>AB+CD

    Tương tự ta cũng chứng minh được AC+BD>AD+BC

    Vậy: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

    Bài 10 trang 90 SBT Toán 8 Tập 1: Thả diều là một trò chơi dân gian của nhiều trẻ em ở Việt Nam cũng như ở nhiều nước trên thế giới. Một tứ giác ABCD với AB=AD,BC=CD gọi là hình “chiếc diều” (Hình 9)

    a)  So sánh B^ và D^.

    b) Tìm mối liên hệ giữa hai đường chéo AC và BD

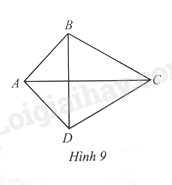
    Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 7)

    Lời giải:

    Gọi O là giao điểm của hai đường chéo AC và BD

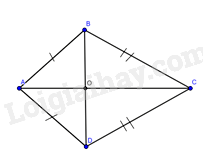
     Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 8)

    a)  ΔABC=ΔADC (c-c-c). suy ra ABC^=ADC^

    b)  ΔABC=ΔADC nên BAO^=DAO^

    ΔABO=ΔADo. Suy ra AOB^=AOD^

    Mà AOD^+AOB^=180∘ nên AOB^=AOD^=90∘

    Vậy AC⊥BD.

    Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

    Bài 3: Hình thang cân

    Bài 4: Hình bình hành

    Bài 5: Hình chữ nhật

    Bài 6: Hình thoi

    Bài 7: Hình vuông

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,313 15/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: