Giải Toán 6 Bài tập cuối chương 1 (Cánh diều)
Lời giải bài tập Toán lớp 6 Bài tập cuối chương 1 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6.
Giải Toán 6 Bài tập cuối chương 1
Bài tập
Toán lớp 6 trang 59 Bài 1: Thực hiện các phép tính sau:
a) 4 . 25 – 12 . 5 + 170 : 10;
c) 12 : {400 : [500 – (125 + 25 . 7)]};
d) 168 + {[2 . (24 + 32) – 2560] : 72}.
Lời giải:
a) 4 . 25 – 12 . 5 + 170 : 10
= 100 – 60 + 17
= 40 + 17
= 57.
b) (7 + 33 : 32) . 4 – 3
= (7 + 33 – 2) . 4 – 3
= (7 + 31) . 4 – 3
= (7 + 3) . 4 – 3
= 10 . 4 – 3
= 40 – 3 = 37.
c) 12 : {400 : [500 – (125 + 25 . 7)]}
= 12 : {400 : [500 – (125 + 175)]}
= 12 : [400 : (500 – 300)]
= 12 : (400 : 200)
= 12 : 2
= 6.
d) 168 + {[2 . (24 + 32) – 2560] : 72}
= 168 + {[2 . (16 + 9) – 1] : 49}
= 168 + [(2. 25 – 1) : 49]
= 168 + [(50 – 1) : 49]
= 168 + (49 : 49)
= 168 + 1 = 169.
Toán lớp 6 trang 59 Bài 2: Gọi P là tập hợp các số nguyên tố. Chọn kí hiệu thích hợp cho :
c) a P với a = 3 . 5 . 7 . 9 + 20;
d) b P với b = 5 . 7 . 11 + 13 . 17.
Lời giải:
Ta có: P là tập hợp các số nguyên tố.
a) Vì 2 chỉ có hai ước là 1 và chính nó nên 2 là số nguyên tố hay 2 thuộc P.
Do đó 2 P.
b) Vì 47 chỉ có hai ước là 1 và 47, nên 47 là số nguyên tố hay 47 thuộc P.
Do đó 47 P.
c) Ta có: a = 3 . 5 . 7 . 9 + 20 = 15 . 7 . 9 + 20 = 105 . 9 + 20 = 945 + 20 = 965
Vì 965 : 5 = 193 nên số 965 ngoài có hai ước là 1 và 965, còn có thêm ít nhất một ước nữa là 5 nên 965 hay a là hợp số.
Do đó a không phải là số nguyên tố nên a không thuộc P.
Vậy a P.
d) Ta có: b = 5 . 7 . 11 + 13 . 17 = 35 . 11 + 221 = 385 + 221 = 606
Vì 606 : 6 = 101 nên số 606 ngoài có hai ước là 1 và 606, còn có thêm ít nhất một ước nữa là 6 nên 606 là hợp số hay b là hợp số.
Do đó b không phải là số nguyên tố nên b không thuộc P.
Vậy b P.
Toán lớp 6 trang 59 Bài 3: Phân tích các số sau ra thừa số nguyên tố:
Lời giải:
Ta có thể phân tích một số ra thừa số nguyên tố bằng cách viết "theo cột dọc" hoặc "rẽ nhánh".
a) Ta có:
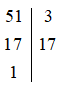
Vậy 51 = 3 . 17.
b) Ta có:
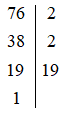
Vậy 76 = 2 . 2 . 19 = 22 . 19.
c) Ta có:

Vậy 225 = 3 . 3 . 5 . 5 = 32 . 52.
d) Ta có: 1 800 = 10 . 180
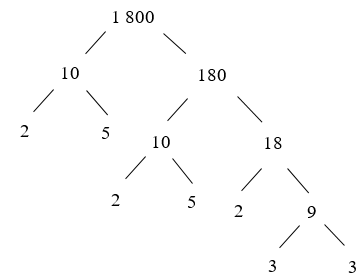
Vậy 1 800 = 2 . 5 . 2 . 5 . 2 . 3 . 3
= 23 . 32 . 52.
Toán lớp 6 trang 59 Bài 4: Tìm ƯCLN của hai số:
Lời giải:
a) 40 và 60
Ta có:
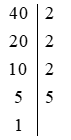
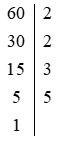
Do đó: 40 = 2 . 2 . 2 . 5 = 23 . 5
60 = 2 . 2 . 3 . 5 = 22 . 3 . 5
Các thừa số nguyên tố chung của 40 và 60 là 2 và 5
Số 2 có số mũ nhỏ nhất là 2; số 5 có số mũ nhỏ nhất là 1
Vậy ƯCLN(40, 60) = 22 . 51 = 4 . 5 = 20.
b) 16 và 124
Ta có: 16 = 24
Lại có

Do đó: 124 = 2 . 2 . 31 = 22 . 31
Thừa số nguyên tố chung của 16 và 124 là 2, với số mũ nhỏ nhất là 2.
Vậy ƯCLN(16, 124) = 22 = 4.
c) 41 và 47
Ta có: số 41 chỉ có hai ước là 1 và 41 nên 41 là số nguyên tố
Số 47 chỉ có hai ước là 1 và 47 nên 47 cũng là số nguyên tố
Do đó 41 và 47 là hai số nguyên tố cùng nhau.
Vậy ƯCLN(41, 47) = 1.
Toán lớp 6 trang 59 Bài 5: Tìm BCNN của các số sau
Lời giải:
a) 72 và 540
Ta có:
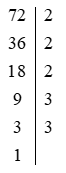

Do đó: 72 = 2 . 2 . 2 . 3 . 3 = 23 . 32
540 = 2 . 2 . 3 . 3 . 3 . 5 = 22 . 33 . 5
Các thừa số nguyên tố chung và riêng của 72 và 540 là 2, 3, 5
Số hai có số mũ lớn nhất là 3; số 3 có số mũ lớn nhất là 3; số 5 có số mũ lớn nhất là 1.
Vậy BCNN(72, 540) = 23 . 33 . 51
= 8 . 27 . 5 = 1 080.
b) 28, 49, 64
Ta có: 28 = 4 . 7 = 22 . 7
49 = 72; 64 = 26
Các thừa số nguyên tố chung và riêng của 28, 49 và 64 là 2, 7
Số 2 có số mũ lớn nhất là 6, số 7 có số mũ lớn nhất là 2.
Vậy BCNN(28, 49, 64) = 26 . 72 = 64 . 49 = 3 136.
c) 43 và 53
Ta có: 43 chỉ có hai ước là 1 và 43 nên 43 là số nguyên tố
53 chỉ có hai ước là 1 và 53 nên nó cũng là số nguyên tố
Do đó 43 và 53 là hai số nguyên tố cùng nhau.
Vậy BCNN(43, 53) = 43 . 53 = 2 279.
Lời giải:
Người ta dựng cột điện dọc theo hai bên của một con đường nên ta tính số cột điện cần phải dựng thêm mới trong một bên trước, sau đó nhân đôi lên, ta được tổng tất cả số cột điện mới cần dựng trên cả con đường.
Do số cột điện cũ dựng ở một bên đường được bắt đầu dựng từ đầu đường tới hết con đường và các cột điện được dựng cách nhau 75 m nên vị trí dựng các cột điện này là bội của 75 và không quá 1500.
Mà các bội của 75 và không quá 1500 là: 0; 75; 150; 225; 300; 375; 450; 525; 600; 675; 750; 825; 900; 975; 1050; 1125; 1200; 1275; 1350; 1425; 1500.
Do đó ta có 21 cột điện cũ được dựng một bên đường (thứ tự từ cột 1 đến cột 21 tương ứng với các vị trí đặt cột từ vị trí 0 m đến 1500 m).
Để tăng cường ánh sáng, người ta dựng lại các cột điện cũng bắt đầu từ đầu đường, cách nhau 50 m và tận dụng lại các cột cũ không phải dời đi, có nghĩa các vị trí cột cũ không phải dời đi là các bội chung của 50; 75 và không quá 1500.
Ta có: 50 = 2 . 25 = 2 . 52; 75 = 3 . 25 = 3 . 52
Suy ra BCNN(50, 75) = 2 . 3 . 52 = 150.
Do đó ta có các bội chung của 50; 75 và không quá 1500 là bội của BCNN(50,75) = 150 và không quá 1500, đó là: 0; 150; 300; 450; 600; 750; 900; 1050; 1200; 1350; 1500.
Nên ta có 11 cột cũ được giữ lại tận dụng, tương ứng với thứ tự các cột điện cũ ở một bên là cột 1; 3; 5; 7; 9; 11; 13; 15; 17; 19; 21.
Mà khoảng cách giữa các cột cũ là đều nhau và bằng 150 m và có 10 khoảng cách cần dựng thêm cột điện mới.
Cho nên ta cần dựng thêm 2 cột điện mới ở vị trí cộng thêm 50 m và 100 m trong từng khoảng cách giữa hai cột cũ được giữ lại.
Do đó, ở một bên đường, ta cần dựng thêm: 2 . 10 = 20 (cột điện mới)
Suy ra ở cả hai bên đường, ta cần dựng thêm số cột điện mới là:
20 . 2 = 40 (cột điện mới)
Tổng chi phí cần thiết để hoàn thành dựng cột điện mới cho con đường là:
4 000 000 . 40 = 160 000 000 (đồng)
Vậy tổng chi phí cần thiết để hoàn thành dựng cột điện mới cho con đường là 160 triệu đồng.
 a) Viết tập hợp A gồm tám hành tinh trong hệ Mặt Trời.
a) Viết tập hợp A gồm tám hành tinh trong hệ Mặt Trời.
b) Sắp xếp kích thước của tám hành tinh trong hệ Mặt Trời theo thứ tự tăng dần.
Lời giải:
a) Tám hành tinh trong hệ Mặt Trời là: Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.
Do đó ta viết tập hợp A là:
A = {Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương}.
b) Quan sát bảng kích thước của các hành tinh:
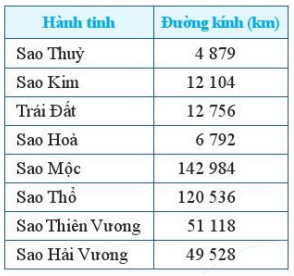 Vì 4 879 < 6 792 < 12 104 < 12 756 < 49 528 < 51 118 < 120 536 < 142 984.
Vì 4 879 < 6 792 < 12 104 < 12 756 < 49 528 < 51 118 < 120 536 < 142 984.
Khi đó ta có sắp xếp kích thước của các hành tinh tương ứng là:
Sao Thuỷ < Sao Hỏa < Sao Kim < Trái Đất < Sao Hải Vương < Sao Thiên Vương < Sao Thổ < Sao Mộc.
Vậy kích thước của các hành tinh trong hệ Mặt Trời được sắp xếp theo thứ tự tăng dần như sau: Sao Thuỷ; Sao Hỏa; Sao Kim; Trái Đất; Sao Hải Vương; Sao Thiên Vương; Sao Thổ; Sao Mộc.
c)
+ Bốn hành tinh có kích thước nhỏ là: Sao Thủy, Sao Hỏa, Sao Kim, Trái Đất.
Nên ta viết tập hợp B là:
B = {Sao Thủy; Sao Hỏa; Sao Kim; Trái Đất}
+ Bốn hành tinh có kích thước lớn là: Sao Hải Vương, Sao Thiên Vương, Sao Thổ, Sao Mộc.
Nên ta viết tập hợp C là:
C = {Sao Hải Vương; Sao Thiên Vương; Sao Thổ; Sao Mộc}.
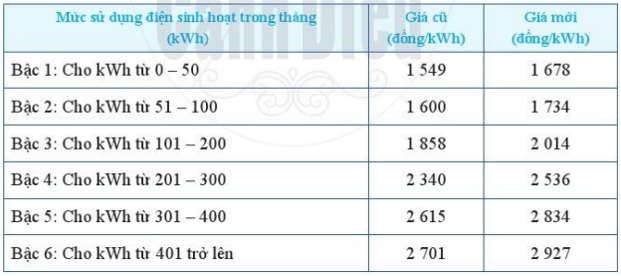 a) Trong tháng 02/2019, gia đình bác Vân tiêu thụ 540 kWh. Gia đình bác Vân phải trả bao nhiêu tiền?
a) Trong tháng 02/2019, gia đình bác Vân tiêu thụ 540 kWh. Gia đình bác Vân phải trả bao nhiêu tiền?
Lời giải:
a) Trong tháng 02/2019 gia đình bác Vân vẫn thanh toán tiền điện theo giá cũ.
Với việc tiêu thụ điện là 540 kWh, gia đình bác Vân đã trải qua cả 6 mức sử dụng điện sinh hoạt.
Do đó để tính giá tiền điện gia đình bác Vân phải trả, ta tính giá tiền trong từng bậc tiêu thụ rồi lấy tổng tất cả, ta được giá tiền bác Vân phải trả.
Giá tiền điện bậc 1 (50 kWh từ kWh thứ 1 đến 50):
1 549 . 50 = 77 450 (đồng)
Giá tiền điện bậc 2 (50 kWh từ kWh thứ 51 đến 100):
1 600 . 50 = 80 000 (đồng)
Giá tiền điện bậc 3 (100 kWh từ kWh thứ 101 đến 200):
1 858 . 100 = 185 800 (đồng)
Giá tiền điện bậc 4 (100 kWh từ kWh thứ 201 đến 300):
2 340 . 100 = 234 000 (đổng)
Giá tiền điện bậc 5 (100 kWh từ kWh thứ 301 đến 400)
2 615 . 100 = 261 500 (đồng)
Ở bậc 6 (từ kWh thứ 401 đến 540), nhà bác Vân tiêu thụ số kWh điện là:
(540 – 401) : 1 + 1 = 140 (kWh) (công thức tính số số hạng)
Giá tiền điện bậc 6 (140 kWh từ kWh thứ 401 đến 540)
2 701 . 140 = 378 140 (đồng)
Tổng số tiền điện gia đình bác Vân phải trả trong tháng 02/2019 là:
77 450 + 80 000 + 185 800 + 234 000 + 261 500 + 378 140 = 1 216 890 (đồng)
Vậy trong tháng 02/2019, gia đình bác Vân tiêu thụ 540 kWh thì gia đình bác Vân phải trả 1 216 890 đồng.
b) Trong tháng 04/2019, gia đình bác Vân phải thanh toán tiền điện theo giá mới
Do đó, ta cần tính tiền trong từng mức theo giá mới:
Giá tiền điện bậc 1 (50 kWh từ kWh thứ 1 đến 50):
1 678 . 50 = 83 900 (đồng)
Giá tiền điện bậc 2 (50 kWh từ kWh thứ 51 đến 100):
1 734 . 50 = 86 700 (đồng)
Giá tiền điện bậc 3 (100 kWh từ kWh thứ 101 đến 200):
2 014 . 100 = 201 400 (đồng)
Giá tiền điện bậc 4 (100 kWh từ kWh thứ 201 đến 300):
2 536 . 100 = 253 600 (đổng)
Giá tiền điện bậc 5 (100 kWh từ kWh thứ 301 đến 400)
2 834 . 100 = 283 400 (đồng)
Ở bậc 6 (từ kWh 401 đến 540), nhà bác Vân tiêu thụ số kWh điện là:
(540 – 401) : 1 + 1 = 140 (kWh) (công thức tính số số hạng)
Giá tiền điện bậc 6 (140 kWh từ kWh thứ 401 đến 540)
2 927 . 140 = 409 780 (đồng)
Tổng số tiền điện gia đình bác Vân phải trả trong tháng 04/2019 là:
83 900 + 86 700 + 201 400 + 253 600 + 283 400 + 409 780 = 1 318 780 (đồng)
Vậy nếu tháng 4/2019, gia đình bác Vân vẫn tiêu thụ 540 kWh thì theo giá mới, số tiền phải trả tăng lên 1 318 780 đồng.
Lý thuyết Toán 6 Tổng hợp lý thuyết Chương 1 – Cánh diều
1. Tập hợp
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
Ví dụ:
+ Tập hợp các đồ vật (sách, bút) đặt trên bàn.
+ Tập hợp học sinh lớp 6A.
2. Kí hiệu và cách viết tập hợp
Tên tập hợp đượA viết bằng chữ cái in hoa như: A, B, C,…
Ví dụ:
+ Tập hợp A gồm các số tự nhiên nhỏ hơn 5
Ta viết: A = {0; 1; 2; 3; 4}
Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
Chẳng hạn, với tập A ở trên, ta có thể viết như sau:
A = {2; 3; 1; 4; 0}
3. Phần tử thuộc tập hợp
Kí hiệu: ∈ (thuộc) và ∉ (không thuộc)
Ví dụ: Cho tập hợp B = {2; 3; 5; 6}
- Số 2 là phần tử của tập hợp B, ta nói phần tử 2 (số 2) thuộc tập hợp B, viết là 2 ∈ B
- Ta thấy số 4 không là phần tử của tập hợp B, ta viết 4 ∉ B, đọc là 4 không thuộc B.
4. Cách cho tập hợp
Có hai cách cho một tập hợp
4.1 Liệt kê các phần tử của tập hợp.
Ví dụ: Quan sát các số được cho ở hình dưới:

Gọi A là tập hợp các số đó.
Các phần tử của tập hợp A là: 0; 1; 2; 3; 4
Ta viết: A = {0; 1; 2; 3; 4}.
4.2 Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ví dụ: Các phần tử của tập hợp A ở trên đều là các số tự nhiên nhỏ hơn 5. Ta có thể viết:
A = {x| x là số tự nhiên nhỏ hơn 5}.
4.3 Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
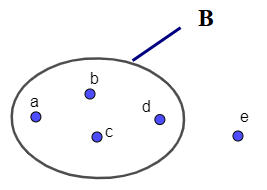
• Ngoài ra ta còn minh họa tập hợp bằng một vòng tròn kín, mỗi phần tử của tập hợp được biểu diễn bằng 1 dấu chấm bên trong vòng tròn kín đó, còn phần tử không thuộc tập hợp được biểu diễn bởi một dấu chấm bên ngoài vòng kín. Cách minh họa tập hợp như trên gọi là biểu đồ Ven (Venn).
Ví dụ: Tập hợp B trong hình vẽ là B = {a; b; c; d}; e ∉ B
5. Tập hợp và tập hợp
Các số 0, 1, 2, 3, 4 … là các số tự nhiên.
Tập hợp các số tự nhiên được kí hiệu là , tức là = {0; 1; 2; 3; 4; …}.
Tập hợp các số tự nhiên khác 0 được kí hiệu là , tức là = {1; 2; 3; 4; …}.
6. Biểu diễn một số tự nhiên trên tia số
Các số tự nhiên được biểu diễn trên tia số. Mỗi số tự nhiên ứng với một điểm trên tia số.
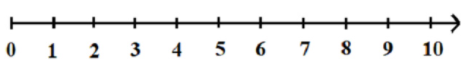
7. Cấu tạo thập phân của số tự nhiên
Số tự nhiên được viết trong hệ thập phân bởi một, hai hay nhiều chữ số. Các chữ số được dùng là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Khi một số gồm hai chữ số trở lên thì chữ số đầu tiên (tính từ trái sang phải) khác 0.
Trong cách viết một số tự nhiên có nhiều chữ số, mỗi chữ số ở những vị trí khác nhau có giá trị khác nhau.
Ví dụ:
+ Số 987 có:
- Chữ số hàng trăm là 9 và có giá trị là 9 x 100
- Chữ số hàng chục là 8 và có giá trị là 8 x 10
- Chữ số hàng đơn vị là 7 và có giá trị là 7
Ta viết: 987 = 9 x 100 + 8 x 10 + 7
+ Kí hiệu là chỉ số tự nhiên có hai chữ số có:
- Chữ số hàng chục là a và có giá trị là a x 10
- Chữ số hàng đơn vị là b và có giá trị là b
Ta viết:
8. Số La Mã
Cách ghi số La Mã:
+ Các số tự nhiên từ 0 đến 10 được ghi bằng số La Mã tương ứng như sau:
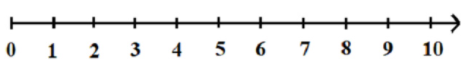
+ Nếu thêm vào bên trái mỗi số ở dòng (1) một chữ số X, ta được số La Mã từ 11 đến 20:

+ Nếu thêm vào bên trái mỗi số ở dòng (1) hai chữ số X, ta được các số La Mã từ 21 đến 30:
![]()
Ví dụ:
+ Số La Mã XIV đọc là mười bốn
+ Số 15 được viết bằng số La Mã là: XV
9. So sánh các số tự nhiên
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì ta viết a < b hay b > a.
Ví dụ: Số 15 nhỏ hơn số 20, ta viết 15 < 20 hay 20 > 15.
+ Với số tự nhiên a cho trước:
Ta viết để chỉ x < a hoặc x = a.
Ta viết để chỉ x > a hoặc x = a.
+ Nếu a < b và b < c thì a < c (tính chất bắc cầu)
Ví dụ: 2 < 3 và 3 < 4 thì 2 < 4
+ Cách so sánh hai số tự nhiên
- Trong hai số tự nhiên có số chữ số khác nhau: Số nào có nhiều chữ số hơn thì lớn hơn, số nào có ít chữ số hơn thì nhỏ hơn.
- Để so sánh hai số tự nhiên có số chữ số bằng nhau, ta lần lượt so sánh từng cặp chữ số trên cùng một hàng (tính từ trái sang phải) cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số tự nhiên chứa chữ số đó lớn hơn.
10. Phép cộng
10.1 Phép cộng hai số tự nhiên
a + b = c
(số hạng) + (số hạng) = (tổng)
Ví dụ: 3 + 2 = 5; 10 + 24 = 34
10.2 Tính chất của phép cộng các số tự nhiên
+ Phép cộng các số tự nhiên có các tính chất: giao hoán, kết hợp, cộng với số 0.
|
Tính chất |
Phát biểu |
Kí hiệu |
|
Giao hoán |
Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi. |
a + b = b + a |
|
Kết hợp
|
Muốn cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba. |
(a + b) + c = a + (b + c) |
|
Cộng với số 0 |
Bất kì số nào cộng với số 0 cũng bằng chính nó. |
a + 0 = 0 + a = a |
+ Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a + b + c có thể được tính theo một trong hai cách sau: a + b + c = (a + b) + c hoặc a + b + c = a + (b + c).
11. Phép trừ
11.1 Phép trừ hai số tự nhiên
a – b = c (a b)
(số bị trừ) – (số trừ) = (hiệu)
Ví dụ: 12 – 7 = 5; 23 – 3 = 20
11.2 Lưu ý
+ Nếu a – b = c thì a = b + c và b = a – c.
+ Nếu a + b = c thì a = c – b và b = c – a.
12. Phép nhân
12.1 Phép nhân hai số tự nhiên
a x b = c
(thừa số) x (thừa số) = (tích)
Ví dụ: 5 x 2 = 10; 20 x 3 = 60
Quy ước:
+ Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.”
Ví dụ: 5 x 2 = 5 . 2
+ Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số
Ví dụ: a x b = a . b = ab hoặc 4. a . b = 4ab
+ Khi nhân hai số có nhiều chữ số, thông thường đặt tính rồi tính, chú ý khi viết các tích riêng (tích riêng thứ hai lùi sang bên trái một cột so với tích riêng thứ nhất, tích riêng thứ ba lùi sang bên trái hai cột so với tích riêng thứ nhất,…)
12.2 Tính chất của phép nhân
Phép nhân các số tự nhiên có các tính chất sau:
+ Giao hoán: a . b = b . a
+ Kết hợp: (a . b) . c = a . (b . c)
+ Nhân với số 1: a . a = 1 . a = a
+ Phân phối đối với phép cộng và phép trừ:
a . (b + c) = a. b + a . c
a . (b – c) = a . b – a . c
Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a. b. c có thể được tính theo một trong hai cách sau:
a . b. c = (a . b) . c hoặc a . b . c = a . (b . c)
13. Phép chia
13.1 Phép chia hết
a : b = q
(số bị chia) : (số chia) = (thương)
Ví dụ: 10 : 2 = 5; 30 : 5 = 6
Chú ý:
+ Nếu a : b = q thì q = bq
+ Nếu a : b = q và q 0 thì a : q = b
+ Thông thường, ta đặt tính chia để thực hiện phép chia.
13.2 Phép chia có dư
Cho hai số tự nhiên a và b với . Khi đó luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó .
Chú ý:
+ Khi r = 0 ta có phép chia hết.
+ Khi ta có phép chia có dư. Ta nói: a chia cho b được thương là q và số dư là r.
Kí hiệu: a : b = q (dư r)
14. Phép nâng lên lũy thừa
Lũy thừa bậc n của a, kí hiệu , là tích của n thừa số a:
với
Trong đó:
a được gọi là cơ số
n được gọi là số mũ.
Quy ước:
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Chú ý:
+ đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bậc n của a”.
+ còn được gọi là “a bình phương” hay “bình phương của a”.
+ còn được gọi là “a lập phương” hay “lập phương của a”.
Lưu ý: Với n là số tự nhiên khác 0, ta có:
15. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
am . an = am + n
Ví dụ: 23 . 24 = 23 + 4 = 27
16. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
am : an = am - n
Quy ước: a0 = 1 .
Ví dụ: 97 : 93 = 97 - 3 = 94
17. Thứ tự thực hiện các phép tính trong biểu thức không chứa dấu ngoặc
+ Khi biểu thức chỉ có các phép tính cộng và trừ (hoặc chỉ có các phép tính nhân và chia), ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Khi biểu thức có các phép tính cộng, trừ, nhân, chia, ta thực hiện phép tính nhân và chia trước, rồi đến cộng và trừ.
+ Khi biểu thức có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
Lũy thừa → Nhân, chia → Cộng, trừ
18. Thứ tự thực hiện các phép tính trong biểu thức chứa dấu ngoặc
+ Khi biểu thức có chứa dấu ngoặc, ta thực hiện các phép tính trong dấu ngoặc trước.
+ Nếu biểu thức chứa các dấu ngoặc ( ), [ ], { } thì thứ tự thực hiện các phép tính như sau: ( ) → [ ] → { }
19. Khái niệm về chia hết
Cho hai số tự nhiên a và b .
Nếu có số tự nhiên q sao cho a = b . q thì ta nói a chia hết cho b.
Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.
Lưu ý:
+ Nếu số dư trong phép chia a cho b bằng 0 thì a chia hết cho b, kí hiệu là .
+ Nếu số dư trong phép chia a cho b khác 0 thì a không chia hết cho b, kí hiệu là .
Lưu ý: Với a là số tự nhiên khác 0 thì:
+ a là ước của a;
+ a là bội của a;
+ 0 là bội của a;
+ 1 là ước của a.
20. Cách tìm bội và ước của một số
20.1 Cách tìm bội của một số
Để tìm các bội của ta có thể lần lượt nhân n với 0, 1, 2, 3, …. Khi đó, các kết quả nhận được đều là bội của n.
20.2 Cách tìm ước của một số
Để tìm các ước của số tự nhiên n lớn hơn 1 ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó, các phép chia hết cho ta số chia là ước của n.
21. Tính chất chia hết của một tổng
Tổng quát: Nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Cụ thể đối với tổng 2 số hạng:
Nếu và thì .
Khi đó ta có: (a + b) : m = a : m + b : m.
22. Tính chất chia hết của một hiệu
Tổng quát: Nếu số bị trừ và số trừ đều chia hết cho cùng một số thì hiệu chia hết cho số đó.
Cụ thể:
Với :
Nếu và thì .
Khi đó ta có: (a – b) : m = a : m – b : m.
23. Tính chất chia hết của một tích
Tổng quát: Nếu một thừa số của tích chia hết cho một số thì tích chia hết cho số đó.
Cụ thể: Nếu thì với mọi số tự nhiên b.
24. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
25. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Nhận xét: Từ dấu hiệu chia hết cho 2 và 5 ở trên, ta thấy những số chia hết cho cả 2 và 5 là những số có chữ số tận cùng là 0.
26. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
27. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
28. Số nguyên tố và hợp số
• Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
• Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Lưu ý:
+ Số 0 và số 1 không là số nguyên tố và cũng không là hợp số.
+ Để chứng tỏ số tự nhiên a lớn hơn 1 là hợp số, ta chỉ cần tìm một ước của a khác 1 và khác a.
Lưu ý: Nếu số nguyên tố p là ước của số tự nhiên a thì p được gọi là ước nguyên tố của a.
Nhận xét: Số nguyên tố nhỏ nhất là số 2 và đó là số nguyên tố chẵn duy nhất.
29. Cách tìm một ước nguyên tố của một số
Để tìm một ước nguyên tố của số tự nhiên n lớn hơn 1, ta có thể làm như sau: lần lượt thực hiện phép chia n cho các số nguyên tố theo thứ tự tăng dần 2, 3, 5, 7, 11, 13, …
Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của n.
30. Phân tích một số ra thừa số nguyên tố
+ Phân tích một số tự nhiên lớn hơn 1 ta thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Lưu ý: Khi phân tích một số ra thừa số nguyên tố ta nên chia mỗi số trong khi phân tích cho ước nguyên tố nhỏ nhất của nó.
Cứ tiếp tục chia như thế cho đến khi được thương là 1.
+ Ta có thể phân tích một số ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”.
Chú ý:
+ Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính số đó.
+ Mọi hợp số đều phân tích được ra thừa số nguyên tố.
+ Thông thường, khi phân tích một số tự nhiên ra thừa số nguyên tố, các ước nguyên tố được viết theo thứ tự tăng dần.
+ Ngoài cách làm như trên, ta cũng có thể phân tích một số ra thừa số nguyên tố bằng cách viết số đó thành tích của hai thừa số một cách linh hoạt.
Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì cuối cùng ta cũng được cùng một kết quả.
31. Ước chung:
Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.
Quy ước: Viết tắt ước chung là ƯC.
Kí hiệu: Tập hợp các ước chung của a và b là ƯC(a, b).
Chú ý: Số tự nhiên n được gọi là ước chung của ba số a, b, c nếu n là ước của cả ba số a, b, c.
32. Ước chung lớn nhất:
Số lớn nhất trong các ước chung của hai số a và b được gọi là ước chung lớn nhất của a và b.
Quy ước: Viết tắt ước chung lớn nhất là ƯCLN.
Kí hiệu: ước chung lớn nhất của a và b là ƯCLN(a, b).
33. Tìm ước chung của hai số khi biết ƯCLN của hai số đó
Ước chung của hai số là ước của ước chung lớn nhất của chúng.
34. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Các bước tìm ƯCLN bằng cách phân tích ra thừa số nguyên tố:
Bước 1. Phân tích mỗi số ra thừa số nguyên tố
Bước 2. Chọn ra các thừa số nguyên tố chung
Bước 3. Với mỗi thừa số nguyên tố chung, ta chọn lũy thừa với số mũ nhỏ nhất
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm.
Chú ý:
+ Nếu hai số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.
+ Nếu thì ƯCLN(a, b) = b. Chẳng hạn, ƯCLN(48, 16) = 16.
35. Hai số nguyên tố cùng nhau
Hai số nguyên tố cùng nhau là hai số có ước chung lớn nhất bằng 1.
36. Phân số tối giản
+ Phân số tối giản là phân số có tử và mẫu là hai số nguyên tố cùng nhau.
+ Ta có thể rút gọn một phân số về phân số tối giản bằng cách chia cả tử và mẫu của phân số đó cho ƯCLN của chúng.
37. Bội chung:
Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.
Quy ước: Viết tắt bội chung là BC.
Kí hiệu: Tập hợp các bội chung của a và b là BC(a, b).
Chú ý: Số tự nhiên n được gọi là bội chung của ba số a, b, c nếu n là bội của cả ba số a, b, c. Ta kí hiệu: Tập hợp các bội chung của a, b, c là BC(a, b, c).
38. Bội chung nhỏ nhất:
Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.
Quy ước: Viết tắt bội chung nhỏ nhất là BCNN.
Kí hiệu: bội chung nhỏ nhất của a và b là BCNN(a, b).
Chú ý:
+ Số nhỏ nhất khác 0 trong các bội chung của ba số a, b, c được gọi là bội chung nhỏ nhất của ba số a, b, c.
+ Kí hiệu: bội chung nhỏ nhất của a, b, c là BCNN(a, b, c).
+ Bội chung nhỏ nhất của hai số nguyên tố cùng nhau bằng tích của hai số đó.
39. Tìm bội chung thông qua BCNN
+ Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.
+ Để tìm bội chung của nhiều số, ta có thể lấy bội chung nhỏ nhất của chúng lần lượt nhân với 0, 1, 2, …
40. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Các bước tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố
Bước 1: Phân tích mỗi số ra thừa số nguyên tố
Bước 2: Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng
Bước 3: Với mỗi thừa số nguyên tố chung và riêng, ta chọn lũy thừa với số mũ lớn nhất
Bước 4: Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm.
Chú ý: Nếu thì BCNN(a, b) = a. Chẳng hạn: BCNN(48, 16) = 48.
41. Ứng dụng bội cung nhỏ nhất vào cộng, trừ các phân số không cùng mẫu
Để tính tổng (hoặc hiệu) hai hay nhiều phân số không cùng mẫu, ta có thể làm như sau:
+ Quy đồng mẫu số hai phân số bằng cách chọn mẫu chung là BCNN của các mẫu.
+ Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
+ Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng (trừ) hai hay nhiều phân số có cùng mẫu.
Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Cánh diều
- Soạn văn lớp 6 (ngắn nhất) - Cánh diều
- Bố cục tác phẩm Ngữ văn 6 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Văn mẫu lớp 6 – Cánh Diều
- Giải VBT Luyện viết Ngữ văn lớp 6 – Cánh diều
- Giải sgk Lịch Sử 6 – Cánh Diều
- Giải sbt Lịch Sử 6 – Cánh Diều
- Giải VBT Lịch sử 6 – Cánh diều
- Lý thuyết Lịch sử lớp 6 – Cánh diều
- Giải sbt Địa Lí 6 – Cánh Diều
- Giải sgk Địa Lí 6 – Cánh Diều
- Lý thuyết Địa Lí 6 – Cánh Diều
- Giải VBT Địa lí 6 – Cánh diều
- Giải sgk GDCD 6 – Cánh Diều
- Lý thuyết GDCD 6 – Cánh diều
- Giải sbt Giáo dục công dân 6 – Cánh diều
- Giải sgk Công nghệ 6 – Cánh Diều
- Lý thuyết Công nghệ 6 – Cánh Diều
- Giải sgk Khoa học tự nhiên 6 – Cánh Diều
- Giải sbt Khoa học tự nhiên 6 – Cánh Diều
- Lý thuyết Khoa học tự nhiên 6 – Cánh Diều
- Giải sgk Tin học 6 – Cánh Diều
- Lý thuyết Tin học 6 – Cánh Diều
- Giải sgk Tiếng Anh 6 - ilearn Smart World
- Ngữ pháp Tiếng Anh 6 i-learn Smart World
- Trọn bộ Từ vựng Tiếng Anh 6 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 6 - iLearn Smart World
- Bài tập Tiếng Anh 6 iLearn Smart World theo Unit có đáp án
