Nội dung bài viết

    Xem thêm

    Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S

    Lời giải Bài 9 trang 61 Toán lớp 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.

    1 2,031 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán lớp 10 Bài tập cuối chương 3

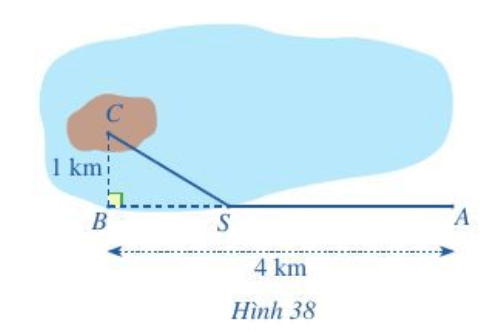
    Bài 9 trang 61 Toán lớp 10 Tập 1: Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.

    Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S

    Lời giải:

    Gọi số ki-lô-mét đường dây điện từ vị trí B đến vị trí S là x (km) (x > 0).

    Khi đó, ta có: SA = AB – BS = 4 - x (km) (Ta có 4 – x > 0 ⇔ x < 4)

    Số tiền công thiết kế trên đoạn đường SA là: 3(4 – x) (triệu đồng)

    Xét ∆CBS vuông tại B, có:

    CS2 = BS2 + BC2 (định lý Py – ta – go)

    CS2 = x2 + 12 = x2 + 1

    CS = x2+1 (km)

    Số tiền công thiết kế trên đoạn đường CS là: 5x2+1 (triệu đồng)

    Tổng số tiền công thiết kế đường dây điện trên cả quãng đường AC là:

    5x2+1+34−x (triệu đồng)

    Vì tổng số tiền công là 16 triệu đồng nên ta có phương trình:

    5x2+1+34−x=16

    ⇔5x2+1=3x+4 (1)

    Điều kiện 3x + 4 ≥ 0 ⇔ x≥−43

    Phương trình (1) ⇔ 25(x2 + 1) = (3x + 4)2

    ⇔ 25x2 + 25 = 9x2 + 24x + 16

    ⇔ 16x2 - 24x + 9 = 0

    ⇔x=34=0,75 (thỏa mãn điều kiện)

    Do đó số ki-lô-mét đường dây từ vị trí A đến S là 4 – 0,75 = 3,25 km.

    Số ki-lô-mét đường dây từ vị trí S đến C là: x2+1=0,752+1=1,25 (km).

    Vậy tổng số ki-lô-mét đường dây đã thiết kế là 3,25 + 1,25 = 4,5 (km).

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Bài 1 trang 60 Toán lớp 10 Tập 1: Tìm tập xác định của mỗi hàm số sau...

    Bài 2 trang 60 Toán lớp 10 Tập 1: Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hóa được sản xuất...

    Bài 3 trang 60 Toán lớp 10 Tập 1: Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau...

    Bài 4 trang 60, 61 Toán lớp 10 Tập 1: Quan sát đồ thị hàm số bậc hai y = ax2 + bx + c ở Hình 37a và Hình 37b...

    Bài 5 trang 61 Toán lớp 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau: a) y = x2 – 3x – 4...

    Bài 6 trang 61 Toán lớp 10 Tập 1: Lập bảng xét dấu của mỗi tam thức bậc hai sau: a) f(x) = – 3x2 + 4x – 1...

    Bài 7 trang 61 Toán lớp 10 Tập 1: Giải các bất phương trình sau: a) 2x2 + 3x + 1 ≥ 0...

    Bài 8 trang 61 Toán lớp 10 Tập 1: Giải các phương trình sau: a) x+2=x...

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

    Bài 2: Giải tam giác

    Bài 3: Khái niệm vectơ

    Bài 4: Tổng và hiệu của hai vectơ

    Bài 5: Tích của một số với một vectơ

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,031 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: