Giáo án Ôn tập chương 3 mới nhất - Toán 12

Giáo án Toán 12 Ôn tập chương 3

Trường:…………………………….. Tổ: TOÁN Ngày soạn: …../…../2021 Tiết:

Họ và tên giáo viên: …………………………… Ngày dạy đầu tiên:……………………………..

 

Môn học/Hoạt động giáo dục: Toán - HH: 12

Thời gian thực hiện: ..... tiết

I. MỤC TIÊU

1. Kiến thức

Giúp học sinh củng cố các kiến thức:

- Véctơ trong không gian  Oxyz và các phép toán vectơ, phương trình mặt cầu.

- Phương trình mặt phẳng  trong không gian Oxyz.

- Phương trình đường phẳng trong không gian Oxyz.

2. Năng lực

a) Năng lực toán

- Năng lực giải quyết vấn đề toán học: HS nhận biết, phát hiện được vấn đề cần giải quyết và biết sử dụng các kiến thức đã được học vào giải quyết các vấn đề.

- Năng lực giao tiếp toán học: Nghe, đọc, hiểu và ghi chép được các thông tin. Sử dụng hiệu quả các kí hiệu toán học. Trình bày, diễn đạt được các ý tưởng và giải pháp toán học trong quá trình trao đổi nhóm.

b) Năng lực chung

- Năng lực tự chủ và tự học: Luôn chủ động, tích cực thực hiện những  công việc của bản thân trong học tập.

- Năng lực giao tiếp và hợp tác: Biết lắng nghe và có phản hồi tích cực trong giao tiếp; nhận biết được ngữ cảnh giao tiếp và đặc điểm, thái độ của đối tượng giao tiếp. Hiểu rõ nhiệm vụ của nhóm; đánh giá được khả năng của mình và tự nhận công việc phù hợp với bản thân.

3. Phẩm chất

- Nghiêm túc, tích cực, chủ động, độc lập và hợp tác trong hoạt động nhóm

- Say sưa, hứng thú trong học tập và tìm tòi nghiên cứu liên hệ thực tiễn

 - Bồi dưỡng đạo đức nghề nghiệp, tình yêu thương con người, yêu quê hương, đất nước. 

 - Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần hợp tác xây dựng cao.

II. THIẾT BỊ DẠY HỌC VÀ HOC LIỆU

Giáo viên: Giáo án, phiếu học tập, phấn, thước kẻ, máy chiếu, máy tính cầm tay ...

Học sinh: Đọc trước bài mới, chuẩn bị bảng phụ, bút viết bảng, máy tính cầm tay, …

III. TIẾN TRÌNH DẠY HỌC

1. HOẠT ĐỘNG 1: MỞ ĐẦU

a) Mục tiêu: Ôn tập và khắc sâu kiến thức đã học về véctơ, phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng trong không gian.

b) Nội dung:

GV hướng dẫn, tổ chức học sinh ôn tập, tìm tòi một số các kiến thức liên quan bài học đã biết:

H1: Trong không gian cho các véctơ $\overrightarrow{a}=(a_1;a_2;a_3),$$\overrightarrow{b}=(b_1;b_2;b_3)$ , tính  $\overrightarrow{a}\pm \overrightarrow{b}$, $\overrightarrow{a}.\overrightarrow{b},\cos \left(\overrightarrow{a},\overrightarrow{b}\right)$?

H2: Nhắc lại phương trình của mặt cầu khi biết tâm và bán kính, phương trình tổng quát của mặt phẳng, phương trình tham số của đường thẳng trong không gian.

c) Sản phẩm: Câu trả lời của học sinh

L1:

$\overrightarrow{a}\pm \overrightarrow{b}=(a_1\pm b_1;a_2\pm b_2;a_3\pm b_3)$

$\overrightarrow{a}.\overrightarrow{b}=a_1.b_1+a_2.b_2+a_3.b_3$

$\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1.b_1+a_2.b_2+a_3.b_3}{\sqrt{a_1^2+a_2^2+a_3^2}.\sqrt{b_1^2+b_2^2+b_3^2}}$

L2: Viết đúng các công thức về các phép toán véctơ trong không gian.

Mặt cầu (S) tâm $I(a;b;c)$, bán kính có phương trình: ${(x-a)}^2+{(y-b)}^2+{(z-c)}^2=R^2$

Mp (P) đi qua $M_0(x_0;y_0;z_0)$ và nhận $\overrightarrow{n}=(A;B;C)$ làm VTPT có phương trình:

$A(x-x_0)+B(y-y_0)+C(z-z_0)=0$

PTTS của đường thẳng $△$ đi qua điểm $M_0(x_0;y_0;z_0)$ và có VTCP $\overrightarrow{a}=(a_1;a_2;a_3)$ có dạng $\left\{\begin{array}{c}x=x_0+t{a}_1\\ y=y_0+t{a}_2\\ z=z_0+t{a}_3\end{array}\right.$

d) Tổ chức thực hiện:

*) Chuyển giáo nhiệm vụ: GV đưa ra các câu hỏi củng cố kiến thức

*) Thực hiện: HS nhận nhiệm vụ suy nghĩ độc lập và thực hiện trả lời các câu hỏi của GV

*) Báo cáo, thảo luận:

GV gọi 2 HS lên bảng trình bày kết quả thảo luận, các HS khác chú ý quan sát sau đó nhận xét, đánh giá, bổ sung cho các phần trình bày của bạn.

*) Đánh giá, nhận xét, tổng hợp:

GV đánh giá phần trình bày của học sinh, đánh giá thái độ làm việc và phần bổ sung nhận xét của các học sinh khác.

GV ghi nhận và tổng hợp kết quả.

GV dẫn dắt vào bài mới: Để các em thuận tiện cho việc giải các bài tập của chương III, hôm nay chúng ta cùng nhau phân chia các dạng bài tập cũng như sẽ đưa ra một số các phương pháp giải cụ thể cho các bài tập cơ bản và nâng cao của chương III. Từ đó sẽ giúp các em dễ dàng hơn trong việc giải các bài tập tại lớp và ở nhà.

2.HOẠT ĐỘNG 2: LUYỆN TẬP

HĐ1. Ôn tập về các phép toán véctơ và kiến thức liên quan

a) Mục tiêu: Giúp học sinh nhớ lại cách làm và thực hiện được cơ bản các dạng bài tập trong SGK.

b)Nội dung: GV yêu cầu đọc SGK và giải bài tập.

       Bài 1: ( trang 91 SGK) Trong không gian cho $A(1;0;0),$$B\left(0;1;0\right),$$C\left(0;0;1\right),$$D\left(-2;1;-1\right)$.

a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.

b) Tìm góc giữa AB và CD.

c) Tính độ dài đường cao của hình chóp A.BCD.

c) Sản phẩm:

Bài 1: a) Phương trình mặt phẳng $\left(ABC\right)$là: $\frac{x}{1}+\frac{y}{1}+\frac{z}{1}=1\iff x+y+z-1=0$ Ta có  $-2+1-1-1\ne 0\Rightarrow D\notin \left(ABC\right)$ Vậy A, B, C, D là bốn đỉnh của một tứ diện. b) $\text{cos}\left(\overrightarrow{AB},\overrightarrow{CD}\right)=\frac{\sqrt{2}}{2}\Rightarrow \left(\overrightarrow{AB},\overrightarrow{CD}\right)={45}^0$ c) $h=d\left(A,\left(BCD\right)\right)=1$.

d) Tổ chức thực hiện

Chuyển giao	- GV đặt vấn đề cách chứng minh bốn điểm A, B, C, D là bốn đỉnh của một tứ diện. - Đặt vấn đề viết phương trình của mặt phẳng theo đoạn chắn, góc giữa hai đường thẳng, độ dài đường cao của hình chóp. - HS xác định các bước cần làm + Viết phương trình mặt phẳng (ABC) + Thay tọa độ điểm D vào phương trình mặt phẳng (ABC) và kết luận. + Xác định góc giữa hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$, từ đó suy ra góc giữa hai đường thẳng AB và CD. + Viết phương trình mặt phẳng (BCD). Từ đó tính khoảng cách từ A đến mặt phẳng (BCD).
Thực hiện	- HS thảo luận theo cặp đôi thực hiện nhiệm vụ - GV theo dõi, hỗ trợ , hướng dẫn các nhóm.
Báo cáo thảo luận	- HS nêu bật được cách viết phương trình mặt phẳng theo đoạn chắn, góc giữa hai vectơ, khoảng cách từ điểm đến mặt phẳng. + Phương trình của mặt phẳng theo đoạn chắn $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\left(abc\ne 0\right)$ +$\overrightarrow{a}=(a_1,a{}_2,a_3),\overrightarrow{b}=(b_1,b_2,b_3)$ và $\overrightarrow{a}\ne \overrightarrow{0},\overrightarrow{b}\ne \overrightarrow{0}$  $\cos (\overrightarrow{a},\overrightarrow{b})==\frac{a_1.b_1+a_2{b}_2+a_3{b}_3}{\sqrt{a_1^2+a_2^2+a_3^2}.\sqrt{b_1^2+{b_2}^2+b_3^2}}$ +$d\left(M,\left(\alpha \right)\right)=\frac{\left|{\text{Ax}}_{\text{0}}+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}};$$M\left(x_0;y_0;z_0\right),\left(\alpha \right):Ax+By+Cz+D=0$ -GV gọi 2 HS lên bảng trình bày lời giải cho bài 1. - HS khác theo dõi, nhận xét, hoàn thiện sản phẩm.
Đánh giá, nhận xét, tổng hợp	- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo. - Chốt kiến thức cách chứng minh bốn điểm không đồng phẳng, tính góc giữa hai đường thẳng thông qua góc giữa hai vectơ, khoảng cách từ một điểm đến một mặt phẳng.

HĐ2. Ôn tập phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng trong không gian.

a) Mục tiêu: Giúp học sinh nhớ lại cách làm và thực hiện được cơ bản các dạng bài tập trong SGK.

b)Nội dung:

Bài 2: ( trang 91 SGK) Trong không gian cho mặt cầu (S) có đường kính AB  biết rằng $A\left(6;2;-5\right),B\left(-4;0;7\right)$.

a) Tìm toạ độ tâm I và tính bán kính r của mặt cầu (S).

b) Lập phương trình mặt cầu (S).

c) Lập phương trình mặt phẳng $\left(\alpha \right)$ tiếp xúc mặt cầu (S) tại điểm A.

Bài 3: (trang 92 SGK) Lập phương trình tham số của đường thẳng

a) Đi qua hai điểm $A\left(1;0;-3\right),B\left(3;-1;0\right)$.

b) Đi qua điểm $M\left(2;3;-5\right)$và song song với đường thẳng d có phương trình $\left\{\begin{array}{l}x=-2+2t\\ y=3-4t\\ z=-5t\end{array}\right.$

c) Sản phẩm:

Học sinh khắc sâu kiến thức về phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng trong không gian. Bài 2: a) $I\left(1;1;1\right),r=IA=\sqrt{62}$ b) Phương trình mặt cầu (S):${\left(x-1\right)}^2+{\left(y-1\right)}^2+{\left(z-1\right)}^2=62$ c) Phương trình mặt phẳng $\left(\alpha \right):5x+y-6z-62=0$ Bài 3: a) Phương trình tham số của đường thẳng AB  là $\left\{\begin{array}{l}x=1+2t\\ y=-t\\ z=-3+3t\end{array}\right.$ b) Phương trình tham số của đường thẳng d  là $\left\{\begin{array}{l}x=2+2t\\ y=3-4t\\ z=-5-5t\end{array}\right.$

d) Tổ chức thực hiện

Chuyển giao	- HS xác định tâm và bán kính của mặt cầu khi biết AB là đường kính - HS lập phương trình mặt cầu - HS xác định được điều kiện tiếp xúc của mặt phẳng và mặt cầu. - HS viết phương trình tham số của đường thẳng khi biết vectơ chỉ phương.
Thực hiện	- HS thảo luận theo cặp đôi thực hiện nhiệm vụ. - GV quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm chưa hiểu nội dung các vấn đề nêu ra
Báo cáo thảo luận	- Các cặp thảo luận đưa ra cách xác định tâm và bán kính của mặt cầu khi biết AB là đường kính. - Thực hiện được bài 2 và viết vào bảng phụ. - Thuyết trình các bước thực hiện.  - Các nhóm khác nhận xét hoàn thành sản phẩm. * Kiến thức ghi nhớ: +Phương trình đường thẳng đi qua điểm  hoặc  và có vectơ chỉ phương $\overrightarrow{AB}$ hoặc vectơ cùng phương với vectơ $\overrightarrow{AB}$. + Viết phương trình đường thẳng đi qua điểm M và song song với một đường thẳng cho trước. $\to$Đường thẳng cần tìm đi qua điểm M và có một vectơ chỉ phương là vectơ chỉ phương đường thẳng đã cho.
Đánh giá, nhận xét, tổng hợp	- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. - Trên cơ sở câu trả lời của học sinh, GV kết luận, và dẫn dắt học sinh ghi nhớ lại kiến thức về phương trình mặt cầu.

HĐ3. Bài tập tổng hợp các kiến thức về phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng trong không gian.

a) Mục tiêu: Giúp học sinh nhớ lại cách làm và thực hiện được cơ bản các dạng bài tập trong SGK.

b)Nội dung:

Bài 5:  ( trang 92 SGK)

Cho mặt cầu  (S): ${(x-3)}^2+{(y+2)}^2+{(z-1)}^2=100$ và mặt phẳng (P): $2\text{x}-2y-z+9=0$. Mặt phẳng (P) cắt (S) theo một đường tròn (C). Hãy xác định toạ độ tâm và bán kính của (C).

Bài 7: (trang 92 SGK)

Cho điểm A(–1; 2; –3), vectơ $\overrightarrow{a}=(6;-2;-3)$ và đường thẳng $d:\left\{\begin{array}{l}x=1+3t\\ y=-1+2t\\ z=3-5t\end{array}\right.$.

a) Viết phương trình mặt phẳng (P) chứa điểm A và vuông góc với giá của $\overrightarrow{a}$.

b) Tìm giao điểm của d và (P).

c) Viết phương trình đường thẳng D đi qua A, vuông góc với giá của vectơ $\overrightarrow{a}$và cắt d.

c) Sản phẩm:

Học sinh vận dụng được các kiến thức đã học vào việc giải các bài tập liên quan . Bài 5: Mặt cầu (S) có tâm $I\left(3;-2;1\right)$ Đường tròn ( C) có tâm J  và bán kính R' J  là hình chiếu của I  trên (P) $\Rightarrow$$J\left(-1;2;3\right)$,$R\text{'}=\sqrt{R^2-d^2}=8$  Bài 7: a) Phương trình mặt phẳng (P): $6\text{x}-2y-3\text{z}+1=0$ b) Giải hệ phương trình $\left\{\begin{array}{l}6\text{x}-2y-3\text{z}+1=0\\ x=1+3t\\ y=-1+2t\\ z=3-5t\end{array}\right.$$\Rightarrow$ $M\left(1;-1;3\right)$ c) D chính là đường thẳng AM $\Rightarrow$ $\Delta :\left\{\begin{array}{l}x=1+2t\\ y=-1-3t\\ z=3+6t\end{array}\right.$

d) Tổ chức thực hiện

Chuyển giao	- HS xác định tâm và bán kính của mặt cầu khi biết phương trình mặt cầu. - Tính khoảng cách từ điểm đến mặt phẳng. - Biết mối liên hệ giữa bán kính mặt cầu, bán kính đường tròn giao tuyến và khoảng cách từ điểm đến mặt phẳng giao tuyến. - Viết phương trình mặt phẳng khi biết 1 điểm và 1 vectơ pháp tuyến. - Tìm giao điểm của đường thẳng và mặt phẳng.
Thực hiện	- HS thảo luận theo cặp đôi thực hiện nhiệm vụ. - GV quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm chưa hiểu nội dung các vấn đề nêu ra
Báo cáo thảo luận	- Các cặp thảo luận đưa ra cách xác định tâm và bán kính của mặt cầu khi biết phương trình mặt cầu - Chỉ ra cách viết phương trình mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn. - Viết phương trình mặt phẳng khi biết 1 điểm và vectơ pháp tuyến. Xác định giao điểm của đường thẳng và mặt phẳng. - Thuyết trình các bước thực hiện.  - Các nhóm khác nhận xét hoàn thành sản phẩm.
Đánh giá, nhận xét, tổng hợp	- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất.

3. HOẠT ĐỘNG 3: VẬN DỤNG.

a) Mục tiêu: Giải quyết một số bài toán về ứng dụng hình tọa độ để làm một số bài toán trong hình không gian và một số bài toán liên quan quỹ tích.

b) Nội dung:

PHIẾU HỌC TẬP 1

Vận dụng  1. Cho hình lập phương $ABC\text{}D.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ có tâm O. Gọi  là tâm của hình vuông $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ và điểm M thuộc đoạn OI sao cho $MO=2MI$ (tham khảo hình vẽ). Khi đó sin của góc tạo bởi hai mặt phẳng $\left(M{C}^{\text{'}}{D}^{\text{'}}\right)$ và (MAB) bằng:

A. $\frac{7\sqrt{85}}{85}$             B. $\frac{17\sqrt{13}}{65}$            C. $\frac{6\sqrt{85}}{85}$              D. $\frac{6\sqrt{13}}{65}$

Vận dụng  2. Cho hình chóp tứ giác đều S.ABCDcó đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết $MN=\frac{a\sqrt{6}}{2}$. Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng (SBD) bằng

A. $\frac{\sqrt{2}}{5}$.           B. $\frac{\sqrt{3}}{3}$.                  C. $\frac{\sqrt{5}}{5}$.              D. $\sqrt{3}$.

Vận dụng  3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng $a\sqrt{2}$ và SA vuông góc với mặt phẳng (ABCD). Gọi $\alpha$ là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu $\tan \alpha =\sqrt{2}$ thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng

A. $30°$.                B. $60°$.                     C. $45°$.                         D. $90°$.

Vận dụng  4. Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có $A^{\text{'}}.ABC$ là tứ diện đều cạnh a. Gọi M, N lần lượt là trung điểm của AA' và BB'. Tính tan của góc giữa hai mặt phẳng (ABC) và (CMN).

A. $\frac{\sqrt{2}}{5}$.                  B. $\frac{3\sqrt{2}}{4}$.              C. $\frac{2\sqrt{2}}{5}$.                  D. $\frac{4\sqrt{2}}{13}$.

PHIẾU HỌC TẬP SỐ 2

Vận dụng  5. Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(6;3;2\right)$, $B\left(2;-1;6\right)$. Trên mặt phẳng (Oxy), lấy điểm $M\left(a;b;c\right)$ sao cho $MA+MB$ bé nhất. Tính $P=a^2+b^3-c^4$.

  A. $P=-48$.           B. $P=33$.           C. $P=48$.       D. $P=129$.

Vận dụng  6. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với $A\left(2;1;3\right)$, $B\left(1;-1;2\right)$, $C\left(3;-6;1\right)$. Điểm $M\left(x;y;z\right)$ thuộc mặt phẳng (Oyz) sao cho $M{A}^2+M{B}^2+M{C}^2$ đạt giá trị nhỏ nhất. Tính giá trị của biểu thức $P=x+y+z$.

 A. $P=6$.                B. $P=-2$.                C. $P=0$.                 D. $P=2$.

c) Sản phẩm: Sản phẩm trình bày của các nhóm.

d) Tổ chức thực hiện:

Chuyển giao	GV: Chia lớp theo nhóm và phát phiếu học tập tiết bài tập HS : Nhận nhiệm vụ.
Thự hiện	Học sinh tìm tòi và nghiên cứu ở nhà
Báo cáo thảo luận	- Các nhóm cử đại diện trình bày ở tiết bài tập cuối - Các nhóm theo dõi và phản biện để làm rõ các vấn đề của bài toán
Đánh giá, nhận xét, tổng hợp.	- Giáo viên nhận xét thái độ làm việc, phương án trả lời các vấn đề . Ghi nhận và khen thưởng các nhóm có câu trả lời tốt, khắc phục những tồn tại của các nhóm làm chưa tốt. - Chốt kiến thức tổng thể của bài học: Ứng dụng hệ tọa độ giải quyết bài toán hình không gian. - Hướng dẫn học sinh về nhà xây dựng các bài toán theo dạng hình, và cách chọn tọa độ cho mỗi dạng toán.

* Hướng dẫn làm bài

Vận dụng  1. Cho hình lập phương $ABC\text{}D.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ có tâm O. Gọi  là tâm của hình vuông $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ và điểm M thuộc đoạn OI sao cho $MO=2MI$ (tham khảo hình vẽ). Khi đó sin của góc tạo bởi hai mặt phẳng (MC'D') và (MAB) bằng

Lời giải

Chọn C

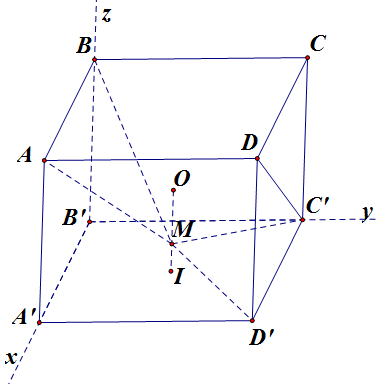
Gắn hệ trục tọa độ như hình vẽ, cạnh hình lập phương là 1, ta được tọa độ các điểm như sau : $M\left(\frac{1}{2};\frac{1}{2};\frac{1}{6}\right)$$,C^{\text{'}}\left(0;1;0\right)$$,D^{\text{'}}\left(1;1;0\right)$ và $A\left(1;0;1\right)$$,B\left(0;0;1\right)$.

Khi đó ${\overrightarrow{n}}_{\left(M{C}^{\text{'}}{D}^{\text{'}}\right)}=\left(0;1;3\right)$$;{\overrightarrow{n}}_{\left(MAB\right)}=\left(0;5;3\right)$ 

nên $\cos \widehat{\left(\left(MAB\right),\left(M{C}^{\text{'}}{D}^{\text{'}}\right)\right)}$$=\frac{\left|5.1+3.3\right|}{\sqrt{5^2+3^2}.\sqrt{1^2+3^2}}$ $=\frac{7\sqrt{85}}{85}$.

Suy ra $\sin \widehat{\left(\left(MAB\right),\left(M{C}^{\text{'}}{D}^{\text{'}}\right)\right)}$$=\sqrt{1-{\left(\frac{7\sqrt{85}}{85}\right)}^2}$$=\frac{6\sqrt{85}}{85}$.

Vận dụng  2. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết $MN=\frac{a\sqrt{6}}{2}$. Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng (SBD) bằng

Lời giải

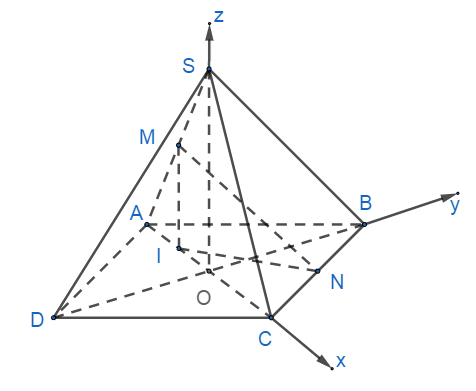
Gọi I hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.

Khi đó $CI=\frac{3}{4}AC=\frac{3a\sqrt{2}}{4}$.

Xét $\Delta CNI$có: $CN=\frac{a}{2}$, $\widehat{NCI}={45}^o$.

Áp dụng định lý cosin ta có:

$$\begin{gathered} NI=\sqrt{C{N}^2+C{I}^2-2CN.CI.\cos {45}^o} \\ =\sqrt{\frac{a^2}{4}+\frac{9a^2}{8}-2.\frac{a}{2}.\frac{3a\sqrt{2}}{4}.\frac{\sqrt{2}}{2}}=\frac{a\sqrt{10}}{4} \end{gathered}$$.

Xét $\Delta MIN$ vuông tại I nên $MI=\sqrt{M{N}^2-N{I}^2}=\sqrt{\frac{3a^2}{2}-\frac{5a^2}{8}}=\frac{a\sqrt{14}}{4}$.

Mà $MI//SO,MI=\frac{1}{2}SO\Rightarrow SO=\frac{a\sqrt{14}}{2}$.

Chọn hệ trục tọa độ Oxyz như hình vẽ:

Ta có: $O\left(0;0;0\right)$, $B\left(0;\frac{\sqrt{2}}{2};0\right)$, $D\left(0;-\frac{\sqrt{2}}{2};0\right)$, $C\left(\frac{\sqrt{2}}{2};0;0\right)$, $N\left(\frac{\sqrt{2}}{4};\frac{\sqrt{2}}{4};0\right)$,

$A\left(-\frac{\sqrt{2}}{2};0;0\right)$, $S\left(0;0;\frac{\sqrt{14}}{4}\right)$, $M\left(-\frac{\sqrt{2}}{4};0;\frac{\sqrt{14}}{4}\right)$.

Khi đó

$\overrightarrow{MN}=\left(\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{4};-\frac{\sqrt{14}}{4}\right)$, $\overrightarrow{SB}=\left(0;\frac{\sqrt{2}}{2};-\frac{\sqrt{14}}{2}\right)$, $\overrightarrow{SD}=\left(0;-\frac{\sqrt{2}}{2};-\frac{\sqrt{14}}{2}\right)$.

Vectơ pháp tuyến mặt phẳng (SBD): $\overrightarrow{n}=\overrightarrow{SB}\wedge \overrightarrow{SD}=\left(-\sqrt{7};0;0\right)$.

Suy ra $\text{sin}\left(MN\text{\hspace{0.17em}},\left(SBD\right)\right)=\frac{\left|\overrightarrow{MN}.\overrightarrow{n}\right|}{\left|\overrightarrow{MN}\right|.\left|\overrightarrow{n}\right|}=\frac{\left|-\sqrt{7}.\frac{\sqrt{2}}{2}\right|}{\sqrt{7}.\frac{\sqrt{6}}{2}}=\frac{\sqrt{3}}{3}$.

Vận dụng  3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng $a\sqrt{2}$ và SA vuông góc với mặt phẳng (ABCD). Gọi $\alpha$ là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu $\tan \alpha =\sqrt{2}$ thì góc giữa hai mặt phẳng (SAC) và SBC) bằng

Lời giải

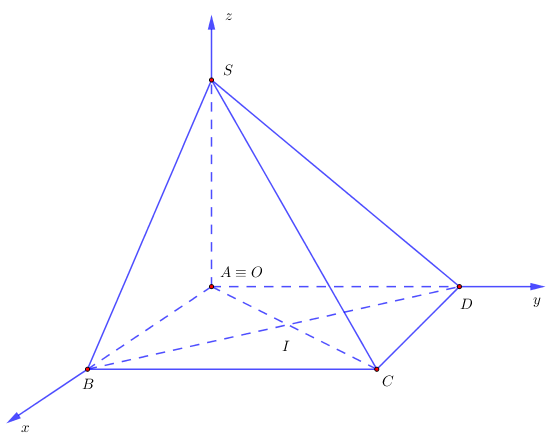
Gọi $I=AC\cap BD$.

Hình vuông ABCD có độ dài đường chéo bằng $a\sqrt{2}$ suy ra hình vuông đó có cạnh bằng a.

Ta có $\left\{\begin{array}{l}\left(SBD\right)\cap \left(ABCD\right)=BD\\ SI\perp BD\\ AI\perp BD\end{array}\right.$$\Rightarrow \widehat{\left(\left(SBD\right);\left(ABCD\right)\right)}=\widehat{\left(SI;AI\right)}=\widehat{SIA}$.

Ta có $\tan \alpha =\tan \widehat{SIA}=\frac{SA}{AI}\iff SA=a$.

Chọn hệ trục tọa độ Oxyz như hình vẽ. Ta có $A\left(0;0;0\right)$, $B\left(a;0;0\right)$, $C\left(a;a;0\right)$, $S\left(0;0;a\right)$.

Khi đó $\overrightarrow{SA}=\left(0;0;-a\right)$; $\overrightarrow{SC}=\left(a;a;-a\right)$; $\overrightarrow{SB}=\left(a;0;-a\right)$.

Mặt phẳng (SAC) có vectơ pháp tuyến ${\overrightarrow{n}}_1=\left(-1;1;0\right)$.

Mặt phẳng (SBC) có vectơ pháp tuyến ${\overrightarrow{n}}_2=\left(1;0;1\right)$.

Suy ra

$\cos \left(\widehat{\left(SAC\right);\left(SBC\right)}\right)=\frac{\left|{\overrightarrow{n}}_1.{\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|.\left|{\overrightarrow{n}}_2\right|}$$=\frac{1}{\sqrt{2}.\sqrt{2}}=\frac{1}{2}$$\Rightarrow \left(\widehat{\left(SAC\right);\left(SBC\right)}\right)=60°$.

Vận dụng  4.  Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có $A^{\text{'}}.ABC$ là tứ diện đều cạnh a. Gọi M, N lần lượt là trung điểm của AA' và BB'. Tính tan của góc giữa hai mặt phẳng (ABC) và (CMN).

Lời giải

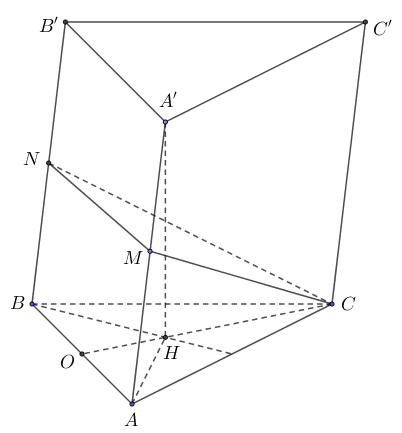
Gọi O là trung điểm của AB. Chuẩn hóa và chọn hệ trục tọa độ sao cho $O\left(0;0;0\right)$,

$A\left(\frac{1}{2};0;0\right)$, $B\left(-\frac{1}{2};0;0\right)$, $C\left(0;\frac{\sqrt{3}}{2};0\right)$, $H\left(0;\frac{\sqrt{3}}{6};0\right)$, $A^{\text{'}}H=\frac{a\sqrt{6}}{3}$$\Rightarrow A^{\text{'}}\left(0;\frac{\sqrt{3}}{6};\frac{\sqrt{6}}{3}\right)$

Ta có $\overrightarrow{AB}=\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$$\Rightarrow B^{\text{'}}\left(-1;\frac{\sqrt{3}}{6};\frac{\sqrt{6}}{3}\right)$. Dễ thấy (ABC) có vtpt $\overrightarrow{n_1}=\left(0;0;1\right)$.

M là trung điểm AA'$\Rightarrow M\left(\frac{1}{4};\frac{\sqrt{3}}{12};\frac{\sqrt{6}}{6}\right)$, N là trung điểm BB'$\Rightarrow N\left(\frac{-3}{4};\frac{\sqrt{3}}{12};\frac{\sqrt{6}}{6}\right)$

$\overrightarrow{MN}=\left(-1;0;0\right)$, $\overrightarrow{CM}=\left(\frac{1}{4};\frac{-5\sqrt{3}}{12};\frac{\sqrt{6}}{6}\right)$

$\Rightarrow$ (CMN) có vtpt $\overrightarrow{n_2}=\left(0;\frac{\sqrt{6}}{6};\frac{5\sqrt{3}}{12}\right)$$=\frac{\sqrt{3}}{12}\left(0;2\sqrt{2};5\right)$

$\cos \phi =$$\frac{5}{\sqrt{33}}$$\Rightarrow \tan \phi =\sqrt{\frac{1}{{\cos }^2\phi }-1}$$=\frac{2\sqrt{2}}{5}$

Vận dụng  5. Trong không gian với hệ tọa độ (Oxyz), cho hai điểm $A\left(6;3;2\right)$, $B\left(2;-1;6\right)$. Trên mặt phẳng (Oxy), lấy điểm $M\left(a;b;c\right)$ sao cho $MA+MB$ bé nhất. Tính $P=a^2+b^3-c^4$.

Lời giải

Phương trình mặt phẳng (Oxy) là: z=0 với A,B nằm cùng phía

Lấy A’ đối xứng với A qua (Oxy) thì $A\text{'}\left(6;3;-2\right)$

Ta có $MA+MB=MA\text{'}+MB\ge A\text{'}B$, dấu bằng khi $A\text{'}B\cap \left(oxy\right)=M$

Khi đó $M(5;2;0)$và $a^2+b^3-c^4=33$

Vận dụng  6. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với $A\left(2;1;3\right)$, $B\left(1;-1;2\right)$, $C\left(3;-6;1\right)$. Điểm $M\left(x;y;z\right)$ thuộc mặt phẳng (Oyz) sao cho $M{A}^2+M{B}^2+M{C}^2$ đạt giá trị nhỏ nhất. Tính giá trị của biểu thức $P=x+y+z$.

Hướng dẫn giải

Gọi  $I\left(2;-2;2\right)$là trọng tâm tam giác ABC thì ta đươc:

$\begin{array}{l}M{A}^2+M{B}^2+M{C}^2={(\overrightarrow{MI}+\overrightarrow{IA})}^2+{(\overrightarrow{MI}+\overrightarrow{IB})}^2+{(\overrightarrow{MI}+\overrightarrow{IC})}^2\\ =3M{I}^2+I{A}^2+I{B}^2+I{C}^2+2\overrightarrow{MI}(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC})\\ =3M{I}^2+I{A}^2+I{B}^2+I{C}^2\end{array}$

 Để $M{A}^2+M{B}^2+M{C}^2$ nhỏ nhất thì M là hình chiếu của I trên mp(Oyz)

Khi đó $M\left(0;-2;2\right)$ và $P=x+y+z=0$

Xem thêm các bài Giáo án Toán lớp 12 hay, chi tiết khác:

Giáo án Hệ tọa độ trong không gian

Giáo án Phương trình mặt phẳng

Giáo án Phương trình đường thẳng trong không gian

Giáo án Ôn tập cuối năm

Giáo án Số phức