Giáo án Giá trị lớn nhất và giá trị nhỏ nhất của hàm số mới nhất - Toán 12
Với Giáo án Giá trị lớn nhất và giá trị nhỏ nhất của hàm số mới nhất Toán lớp 12 được biên soạn bám sát sách Toán 12 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
|
Trường:…………………………….. Tổ:TOÁN Ngày soạn: …../…../2021 Tiết: |
Họ và tên giáo viên: …………………………… Ngày dạy đầu tiên:…………………………….. |
I. MỤC TIÊU
1. Kiến thức
- Biết các khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập hợp số.
- Nắm được qui tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn
- Biết cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, một khoảng.
- Phân biệt việc tìm giá trị lớn nhất, giá trị nhỏ nhất với tìm cực trị của hàm số.
- Dựa vào đồ thị chỉ ra được giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
- Biết vận dụng giá trị lớn nhất, giá trị nhỏ nhất vào giải các bài toán có chứa tham số
- Biết vận dụng giá trị lớn nhất, giá trị nhỏ nhất vào giải các bài toán thực tế.
2. Năng lực
- Năng lực tự học:Học sinh xác định đúng đắn động cơ thái độ học tập; tự đánh giá và điềuchỉnh được kế hoạch học tập; tự nhận ra được sai sót và cách khắc phục sai sót.
- Năng lực giải quyết vấn đề: Biết tiếp nhận câu hỏi, bài tập có vấn đề hoặc đặt ra câu hỏi. Phân tích được các tình huống trong học tập.
- Năng lực tự quản lý: Làm chủ cảm xúc của bản thân trong quá trình học tập vào trong cuộc sống; trưởng nhóm biết quản lý nhóm mình, phân công nhiệm vụ cụ thể cho từng thành viên nhóm, các thành viên tự ý thức được nhiệm vụ của mình và hoàn thành được nhiệm vụ được giao.
- Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.
- Năng lực hợp tác: Xác định nhiệm vụ của nhóm, trách nhiệm của bản thân đưa ra ý kiến đóng góp hoàn thành nhiệm vụ của chủ đề.
- Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học.
3. Phẩm chất
- Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần trách nhiệm hợp tác xây dựng cao.
- Chăm chỉ tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của giáo viên.
- Năng động, trung thực sáng tạo trong quá trình tiếp cận tri thức mới .
- Hình thành tư duy logic, lập luận chặt chẽ và linh hoạt trong quá trình suy nghĩ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
- Kiến thức về giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
- Máy chiếu.
- Bảng phụ.
- Phiếu học tập.
III. TIẾN TRÌNH DẠY HỌC
1. HOẠT ĐỘNG 1: MỞ ĐẦU
a) Mục tiêu: Biết giá trị lớn nhất, giá trị nhỏ nhất của hàm số đơn giảnthông qua đồ thị
b) Nội dung:Giáo viên hướng dẫn, tổ chức học sinh nhận biết giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai thông qua đồ thị
H1- Quan sát đồ thị hãy chỉ giá trị lớn nhất, giá trị nhỏ nhất của hàm (nếu có)?
H2- Vị trí của điểm cách một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
c) Sản phẩm:
Câu trả lời của học sinh
L1- Giá trị lớn nhất của hàm số không có; giá trị nhỏ nhất của của hàm số bằng 1
L2- Không trả lời được
d) Tổ chứcthực hiện:
*) Chuyển giao nhiệm vụ : Giáo viên nêu câu hỏi
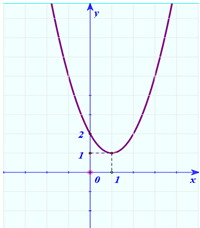
Câu 1. Cho hàm số có đồ thị hình bên. Nhìn vào đồ thị tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của hàm số trên R .

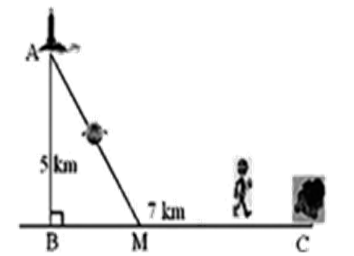
Câu 2.Một ngọn hải đăng đặt tại vị trí có khoảng cách đến bờ biển .Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7km . Người canh hải đăng có thể chèo đò từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h . Vị trí của điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
*) Thực hiện:Học sinh độc lậpsuy nghĩ câu 1 và thảo luận nhóm tìm câu trả lời cho câu 2
*) Báo cáo, thảo luận:
- Giáo viên gọi 1học sinh trình bày câu trả lời của mình (Chỉ trên hình vẽ và giải thích)
- Các học sinh khác nhận xét, bổ sung để hoàn thiện câu trả lời.
*) Đánh giá, nhận xét, tổng hợp:
- Giáo viên đánh giá thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tổng hợp kết quả.
- Dẫn dắt vào bài mới: Thông qua câu hỏi 2 dẫn dắt vào bài; thông qua câu hỏi 1 để đưa ra định nghĩa giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Nội dung bài này sẽ giúp chúng ta sẽ tìm được vị trí của điểm cách một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
Lời giải câu 2. Đặt suy ra với
Ta có Thời gian chèo đò A từ đến M là: (h)
Thời gian đi bộ đi bộ đến C là: (h).
Thời gian từ A đến kho
Khi đó: , cho .
Lập bảng biến thiên, ta thấy thời gian đến kho nhanh nhất khi .
2. HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC
A. KHỞI ĐỘNG
Hoạt động 1. Tình huống xuất phát (mở đầu).
(1) Mục tiêu: Tạo sự tò mò, gây hứng thú cho học sinh về nội dung nghiên cứu, ứng dụng của GTLN, GTNN. Hình dung được những đối tượng sẽ nghiên cứu, áp dụng GTLN, GTNN.
(2) Phương pháp/Kĩ thuật dạy học: Nêu vấn đề
(3) Hình thức tổ chức hoạt động: Hoạt động theo cá nhân, hoạt động theo nhóm nhỏ.
(4) Phương tiện dạy học: Có thể sử dụng Phiếu bài tập hoặc máy chiếu để chiếu nhanh câu hỏi.
(5) Sản phẩm: HS nhớ lại được các kiến thức về cực trị. HS thấy được sự cần thiết của bài học “GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ”. Học sinh đặt ra câu hỏi: trong toán học một hàm số đạt GTLN, GTNN cần thỏa mãn các điều kiện nào? Học sinh mô tả bằng cách hiểu của mình về GTLN, GTNN của hàm số.
Nêu nội dung của Hoạt động 1:
GV: Hỏi HS các bước tìm các cực trị của hàm số.
HS: Nêu câu trả lời.
GV yêu cầu HS quan sát ví dụ và trả lời câu hỏi
Ví dụ: Cho 2 hàm số
Nhận xét về giá trị của hàm số
GV: Đưa ra một số bài toán thực tế
1. Một công ty bất động sản có căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2000000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 50000 đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớt nhất. Hỏi thu nhập có nhất công ty có thể đạt được trong một tháng là bao nhiêu?
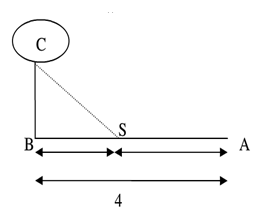
2. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như hình vẽ. Khoảng cách từ đến B là 1km . Bờ biển chạy thẳng từ A đến B với khoảng cách là 4km . Tổng chi phí lắp đặt cho 1km dây điện trên biển là 40 triệu đồng, còn trên đất liền là 20 triệu đồng. Tính tổng chi phí nhỏ nhất để hoàn thành công việc trên(làm tròn đến hai chữ số sau dấu phẩy).
Trong thực tế có rất nhiều bài toán liên quan đến giá trị lớn nhất và giá trị nhỏ nhất. Để giải quyết loại bài toán trên ta nghiên cứu bài học: “GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ”.
B. HÌNH THÀNH KIẾN THỨC
I. Định nghĩa GTLN, GTNN của hàm số
a) Mục tiêu: Học sinh biết được định nghĩa GTLN-GTNN hàm số. Biết cách vận dụng định nghĩa để GTLN-GTNN hàm số.
b) Nội dung:
H1.Cho 2 hàm số
Tìm GTLN-GTNN của các hàm hàm số trên
H2. Gv nêu định nghĩa GTLN-GTNN hàm số
H3. Bài toán 1. Cho hàm số có đồ thị hình bên. Nhìn vào đồ thị tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của hàm số trên R .
c) Sản phẩm:
Cho hàm số xác định trên tập D .
a) Số M được gọi là giá trị lớn nhất của hàm số trên D nếu
Kí hiệu:
b) Số m được gọi là giá trị nhỏ nhất của hàm số trên D nếu
Kí hiệu:
VD: Cho hàm số có bảng biến thiên:
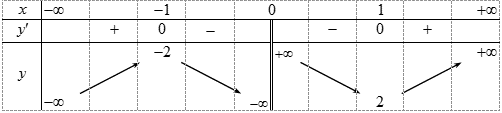
1. Giá trị lớn nhất của hàm số trên khoảng là
2. Giá trị nhỏ nhất của hàm số trên khoảng là
Nhận xét:
1. Trên khoảng (a; b) hàm số đạt cực đại duy nhất, khi đó hàm số đạt giá trị lớn nhất bằng giá trị cực đại của hàm số. Ta có
2. Trên khoảng (a; b) hàm số đạt cực tiểu duy nhất, khi đó hàm số đạt giá trị nhỏ nhất bằng giá trị cực tiểu của hàm số. Ta có
3. PP tìm GTLN, GTNN của hàm số trên tập D: Lập bảng biến thiên hàm số trên D.
d) Tổ chức thực hiện
|
Chuyển giao |
HS thực hiện các nội dung sau - Giải các bài toán đưa ra theo yêu cầu của gv -Hình dung đc khái niệm gtln, gtnn của hàm số - Hiểu định nghĩa gtln, gtnn của hàm số |
|
Thực hiện |
- HS thảo luận thực hiện nhiệm vụ. - GV nêu câu hỏi, quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm chưa hiểu rõ nội dung vấn đề nêu ra |
|
Báo cáo thảo luận |
- Các học sinh đưa ra khái niệm gtln, gtnn của hàm số - Thực hiện được VD và nêu đc gtln, gtnn của hàm số - Thuyết trình các bước thực hiện. |
|
Đánh giá, nhận xét, tổng hợp |
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh - Trên cơ sở câu trả lời của học sinh, GV kết luận, và dẫn dắt học sinh hình thành kiến thức mới về gtln, gtnn của hàm số |
II Cách tính GTLN-GTNN của hàm số trên một đoạn
a) Mục tiêu: Biết tìm GTLN, GTNN của hàm số trên 1 đoạn
b) Nội dung:
H1.Bài toán 1: Tìm GTLN-GTNN của hàm số trên đoạn
H2.Tìm GTLN-GTNN của hàm số trên đoạn
c) Sản phẩm:
|
1.Định lý : Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên một đoạn đó.D 2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn Quy tắc: + Tìm các điểm trên khoảng , tại đó bằng 0 hoặc không xác định. + Tính . + Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có: Bài toán 2: Tìm giá trị nhỏ nhất của hàm số trên đoạn . Giải: Hàm số liên tục trên Ta có ; . Do đó . Bài toán 3:Tìm giá trịlớn nhất trên hàm số đoạn Ta có: , cho Khi đó: , , . Vậy . 3. Chú ý: a) Nếu hàm số đồng biến trên đoạn [a; b] thì: b) Nếu hàm số nghịch biến trên đoạn [a; b] thì c) Hàm số liên tục trên một khoảng có thể không tồn tại GTLN, GTNN trên khoảng đó. |
d) Tổ chức thực hiện
|
Chuyển giao |
- GV yêu cầu học sinh lập bảng biến thiên của trên đoạn từ đó tìm ra GTLN, GTNN của hàm số trên đoạn - HS lập bảng biến thiên và đọc kết quả -GV hỏi về sự tồn tại của GTLN, GTNN của hàm số trên đoạn , từ đó suy ra GTLN, GTNN của hàm số trên đoạn , -Gv yêu cầu học sinh nêu ra các bước tìm GTLN, GTNN của hàm số trên đoạn , |
|
Thực hiện |
- HS thảo luận thực hiện nhiệm vụ - GV theo dõi, hỗ trợ , hướng dẫn |
|
Báo cáo thảo luận |
- HS nêu được sự tồn tại của GTLN, GTNN của hàm số trên đoạn . HS nêu được các bước tìm GTLN, GTNN của hàm số trên đoạn - GV gọi 2HS lên bảng trình bày lời giải cho Bài toán 2 và Bài toán 3- HS khác theo dõi, nhận xét, hoàn thiện sản phẩm |
|
Đánh giá, nhận xét, tổng hợp |
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức và quy tắc bước tìm GTLN, GTNN của hàm số trên đoạn |
3. HOẠT ĐỘNG 3: LUYỆN TẬP
a) Mục tiêu: HS biết áp dụng các kiến thức về tính giá trị lớn nhất giá trị nhỏ nhất trên 1 đoạn, trên một khoảng, trên tập xác định của hàm số vào các bài tập cụ thể
b) Nội dung:
PHIẾU HỌC TẬP 1
Câu 1. Giá trị nhỏ nhất của hàm số trên đoạn là:
A. B. C. D.
Câu 2. Giá trị nhỏ nhất của hàm số trên đoạn
A. B. C. D.
Câu 3. Giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn
A. B.
C. D.
Câu 4. Giá trị lớn nhất của hàm số trên đoạn
A. . B. . C. . D. .
Câu 5. Trên khoảng thì hàm số :
A. Có giá trị nhỏ nhất là B. Có giá trị lớn nhất là
C. Có giá trị nhỏ nhất là D. Có giá trị lớn nhất là
Câu 6. Giá trị lớn nhất của hàm số trên
A. . B. . C. . D. .
Câu 7. Giá trị nhỏ nhất của hàm số trên đoạn bằng:
A. B. C.-3 D.-5
Câu 8. Giá trị lớn nhất của hàm số trên đoạn bằng:
A.0 B. 9 C.1 D.3
Câu 9. Tìm giá trị lớn nhất của hàm số trên đoạn
A. . B.-5 C.5 D. .
Câu 10. Giá trị lớn nhất của hàm số trên đoạn là:
A. B. C. D.
Câu 11. Giá trị nhỏ nhất của hàm số trên đoạn là
A. B. C. D.0
Câu 12. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn là
A. B.
C. D.
Câu 13. Giá trị nhỏ nhất của hàm số . Với bằng
A. 4 B. 2 C. 1 D. 3
Câu 14. Hàm số đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn lần lượt tại . Khi đó bằng:
A.2 . B. 0. C.6 . D. .
Câu 15. Hàm số có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn lần lượt là . Khi đó tích có giá trị bằng:
A. . B.-1 . C. . D.0 .
Câu 16. Hàm số đạt giá trị lớn nhất bằng trên đoạn khi m bằng:
A.-8 B.3 C.-3 D.-6
Câu 17. Tìm giá trị lớn nhất của hàm số ?
A. . B. .
C. . D. .
Câu 18. Giá trị lớn nhất của hàm số trên đoạn bằng.
A. . B. . C. . D. .
Câu 19. Tìm giá trị lớn nhất của hàm số trên đoạn [2; 5]
A. B. C. D.
Câu 20. Tìm giá trị nhỏ nhất của hàm số
A. . B. . C. . D. .
Câu 21. Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số
A. Có giá trị lớn nhất và có giá trị nhỏ nhất.
B. Có giá trị nhỏ nhất và không có giá trị lớn nhất.
C. Có giá trị lớn nhất và không có giá trị nhỏ nhất.
D. Không có giá trị lớn nhất và giá trị nhỏ nhất.
Câu 22. Tìm giá trị lớn nhất của hàm số trên đoạn
A. . B.-5 . C.5 . D. .
Câu 23. Tìm m để hàm số đạt giá trị lớn nhất tại trên đoạn ?
A. . B. . C. . D.
Câu 24. Giá trị lớn nhất của hàm số trên đoạn
A.6 B.10 C.15 D.11
Câu 25. Giá trị nhỏ nhất của hàm số trên là :
A.2 B.-3 C.3 D.-4
Câu 26. Giá trị lớn nhất của hàm số là:
A. . B.4 C.2 D. .
Câu 27. Cho hàm số tìm khẳng định sai trong các khẳng định sau.
A. Hàm số không có giá trị nhỏ nhất. B. Hàm số có giá trị lớn nhất.
C. . D. .
Câu 28. Cho hàm số tìm khẳng định đúng trong các khẳng định sau.
A. Hàm số không có giá trị nhỏ nhất trên R. B. .
C. . D. .
Câu 29. Giá trị lớn nhất của hàm số là:
A.5 B. . C.4 D. .
Câu 30. Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Khi đó giá trị biểu thức
A. . B. . C. . D. .
BẢNG ĐÁP ÁN:
|
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 10 |
|
A |
B |
A |
D |
D |
D |
C |
D |
D |
D |
|
Câu 11 |
Câu 12 |
Câu 13 |
Câu 14 |
Câu 15 |
Câu 16 |
Câu 17 |
Câu 18 |
Câu 19 |
Câu 20 |
|
A |
C |
D |
B |
A |
D |
A |
D |
B |
A |
|
Câu 21 |
Câu 22 |
Câu 23 |
Câu 24 |
Câu 25 |
Câu 26 |
Câu 27 |
Câu 28 |
Câu 29 |
Câu 30 |
|
A |
D |
C |
C |
A |
C |
D |
A |
D |
B |
c) Sản phẩm: Học sinh thể hiện trên bảng nhóm kết quả bài làm của mình
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Chia lớp thành 4 nhóm. Phát phiếu học tập 1 HS:Nhận nhiệm vụ, |
|
Thực hiện |
GV: điều hành, quan sát, hỗ trợ HS: 4 nhóm tự phân công nhóm trưởng, hợp tác thảo luận thực hiện nhiệm vụ. Ghi kết quả vào bảng nhóm. |
|
Báo cáo thảo luận |
Đại diện nhóm trình bày kết quả thảo luận Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo |
4. HOẠT ĐỘNG 4: VẬN DỤNG.
a)Mục tiêu: Giải quyết một số bài toán ứng dụng tính toán tối ưu trong thực tế
b) Nội dung
PHIẾU HỌC TẬP 2
|
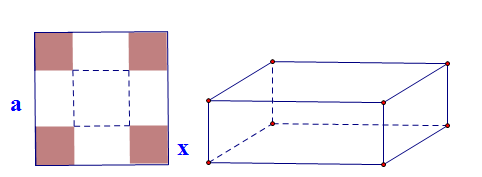
Vận dụng 1: Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở bốn góc bốn hình vuông bằng nhau, rồi gập tấm tôn lại như hình bên để được một cái hộp không nắp. Tính cạnh của hình vuông bị cắt sao cho thể tích của khối hộp là lớn nhất? |
|
Vận dụng 2:
|
Bác A có 200m dây thép dùng để làm hàng rào vườn rau sạch phục vụ gia đình và người thân trong thời gian nghỉ dịch. Bác muốn chia mảnh vườn thành 2 phần, 1 phần hình vuông trồng rau cần, 1 phần hình tròn trồng các loại rau khác. Bác A cắt 200m dây thép đó thế nào để có thể rào đủ 2 phần trồng rau để diện tích trồng lớn nhất? |
|
|
Vận dụng 3: Gia đình nhà An muốn làm 1 bể nước hình trụ thể tích để chưa nước mưa. Đáy làm bằng bê tông giá , thành làm bằng tôn giá , nắp bằng nhôm không gỉ giá . Vậy gia đình an cần chọn kích thước bể như thế nào để tiết kiệm chi phí nhất? |
|
c) Sản phẩm: Sản phẩm trình bày của 4 nhóm học sinh
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Chia lớp thành 4 nhóm. Phát phiếu học tập 2 cuối tiết của bài HS:Nhận nhiệm vụ, |
|
Thực hiện |
Các nhóm HS thực hiện tìm tòi, nghiên cứu và làm bài ở nhà . |
|
Báo cáo thảo luận |
HS cử đại diện nhóm trình bày sản phẩm vào tiết tiếp theo Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. - Chốt kiến thức tổng thể trong bài học. - Hướng dẫn HS về nhà tự xây dựng tổng quan kiến thức đã học bằng sơ đồ tư duy. |
Ngày ...... tháng ....... năm 2021
TTCM ký duyệt
Xem thêm các bài Giáo án Toán lớp 12 hay, chi tiết khác:
Giáo án Sự đồng biến, nghịch biến của hàm số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12