Giáo án Cực trị của hàm số mới nhất - Toán 12
Với Giáo án Cực trị của hàm số mới nhất Toán lớp 12 được biên soạn bám sát sách Toán 12 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 12 Bài 2: Cực trị của hàm số
|
Trường:…………………………….. Tổ:TOÁN Ngày soạn: …../…../2021 Tiết: |
Họ và tên giáo viên: …………………………… Ngày dạy đầu tiên:…………………………….. |
BÀI 2: CỰC TRỊ CỦA HÀM SỐ
Môn học/Hoạt động giáo dục: Toán - GT: 12
Thời gian thực hiện: ....... tiết
I. MỤC TIÊU
1. Kiến thức
Yêu cầu HS cần đạt
- Nắm vững các công thức tính đạo hàm.
- Hiểu được khái niệm cực đại, cực tiểu. Phân biệt được điểm cực trị của hàm số và của đồ thị hàm số; giá trị và điểm cực trị.
- Nắm được điều kiện đủ để hàm số có cực trị.
- Nắm vững hai quy tắc tìm cực trị của hàm số. Bước đầu vận dụng vào giải các bài toán tìm cực trị đơn giản.
- Hiểu được đồ thị và bảng biến thiên, từ đó chỉ ra được các điểm cực trị, giá trị cực trị.
2. Năng lực
- Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập; tự giác tìm hiểu, phân tích để lĩnh hội kiến thức mới và vận dụng vào giải quyết bài tập.
- Năng lực giao tiếp: Tiếp thu kiến thức thông qua trao đổi hoạt động nhóm; Có khả năng báo cáo, phản biện trước tập thể.
- Năng lực tư duy và giải quyết vấn đề: Nhận biết được các điểm cực trị thông qua đồ thị và bảng biến thiên. Áp dụng hợp lí một trong hai quy tắc với các bài toán cụ thể.
- Năng lực sử dụng ngôn ngữ: Học sinh đọc và viết chính xác các kí hiệu của cực trị.
3. Phẩm chất
- Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần trách nhiệm hợp tác xây dựng cao.
- Chăm chỉ tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
- Năng động, trung thực, sáng tạo trong quá trình tiếp cận tri thức mới, có tinh thần hợp tác xây dựng cao.
- Hình thành tư duy logic, lập luận chặt chẽ và linh hoạt trong quá trình suy nghĩ.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
* Thiết bị dạy học: Máy chiếu, máy tính cầm tay, bảng phụ.
* Học liệu: Kế hoạch bài dạy, giáo án, SGK, phiếu học tập...
III. TIẾN TRÌNH DẠY HỌC
1. HOẠT ĐỘNG 1: MỞ ĐẦU
a) Mục tiêu:
- Học sinh nhớ lại các bước tìm khoảng đồng biến, nghịch biến của hàm số.
- Tạo sự hứng thú cho học sinh thông qua việc tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một khoảng từ đồ thị.
- Bước đầu suy nghĩ, tìm hiểu về cực trị của hàm số.
b) Nội dung
H1: Trình bày quy tắc xét tính đơn điệu của hàm số?
H2: Xét tính đơn điệu của các hàm số sau
a. y=−x2+1 b. y=x3(x−3)2
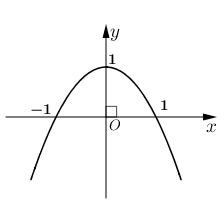
H3: Dựa vào đồ thị hai hàm số trên (hình dưới), hãy chỉ ra các điểm tại đó hàm sốđạt giá trị lớn nhất hoặc nhỏ nhất trên các khoảng cho trước?
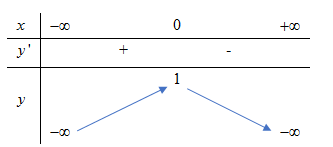
+ Hàm số y=−x2+1 trên R
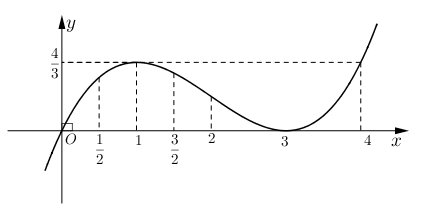
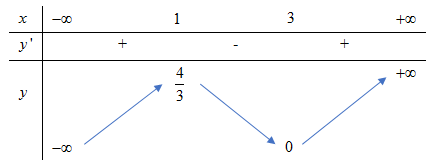
+ Hàm số y=x3(x−3)2 trên các khoảng (0;32) và (2;4)
|
|
|
|
Hình 1 |
Hình 2 |
c) Sản phẩm
Câu trả lời của HS
TL1: Gồm 4 bước
+ Tìm TXĐ
+ Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng không hoặc không xác định
+ Lập BBT
+ Nêu KL về khoảng đồng biến, nghịch biến.
TL2:
* y=−x2+1
1. TXĐ: D=ℝ
2. Ta có y'
3. BBT
4. KL: Hàm số đồng biến trên khoảng , nghịch biến trên khoảng
*
1. TXĐ:
2. Ta có
3. BBT
4. KL: Hàm số đồng biến trên các khoảng và , nghịch biến trên khoảng
TL3:
+ Hình 1: Hàm số không có GTNN, hàm số đạt GTLN là y=1 tại x=0 trên R
+ Hình 2: Hàm số đạt GTLN là tại x=1 trên khoảng , đạt GTNN là y=0 tại x=3 trên khoảng .
* NX: Đểhàm số có GTLN hoặc GTNN trên một khoảng cho trước thì y' phải đổi dấu khi đi qua các điểm đó.
d) Tổ chức thực hiện
* Chuyển giao nhiệm vụ :GVnêu câu hỏi và chiếu hình ảnh cho HS?
* Thực hiện:HS suy nghĩ độc lập
* Báo cáo, thảo luận:
- GV gọi lần lượt 4 HS lên bảng trình bày câu trả lời của mình.
- Các học sinh khác nhận xét, bổ sung.
* Đánh giá, nhận xét, tổng hợp:
- GV đánh giá thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tổng hợp kết quả.
- Đặt vấn đề vào bài: Để giúp các em hiểu được khái niệm cực trị của hàm số và nắm được các quy tắc tính cực trị của hàm số và các bài toán liên quan chúng ta cùng đi tìm hiểu bài học hôm nay: “Bài 2: CỰC TRỊ CỦA HÀM SỐ”
2. HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚI
2.1. HOẠT ĐỘNG 2.1. KHÁI NIỆM CỰC ĐẠI, CỰC TIỂU CỦA HÀM SỐ
a) Mục tiêu: Học sinh hiểu được khái niệm hàm số đạt cực đại, cực tiểu tại một điểm , đồng thời lưu ý các tên gọi liên quan đến cực đại, cực tiểu của hàm số.
b)Nội dung:
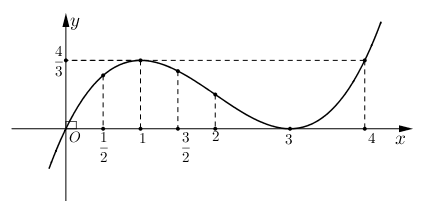
Học sinh quan sát đồ thị hàm số như trên và trả lời câu hỏi:
H1: Dựa vào đồ thị, hãy chỉ ra các điểm tại đó hàm số có giá trị lớn nhất trên khoảng ?
H2: Dựa vào đồ thị, hãy chỉ ra các điểm tại đó hàm số có giá trị nhỏ nhất trên khoảng ?
H3: Phát biểu khái niệm hàm số đạt cực đại, đạt cực tiểu tại một điểm
H4: Nêu tên gọi , , khi hàm số đạt cực đại, đạt cực tiểu tại
c) Sản phẩm:
|
L1:x=1 TL2: x=3 HS đọc SGK phát hiện và nêu định nghĩa và nắm các yếu tố của chú ý ĐỊNH NGHĨA: Cho hàm số xác định và liên tục trên khoảng (có thể a là , b là ) và điểm . a) Nếu tồn tại số h>0 sao cho với mọi và thì ta nói hàm số đạt cực đại tại b) Nếu tồn tại số h>0 sao cho với mọi và thì ta nói hàm số đạt cực tiểu tại CHÚ Ý: 1. Nếu hàm số đạt cực đại (cực tiểu) tại thì được gọi là điểm cực đại (điểm cực tiểu) của hàm số; được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số; điểm được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số. 2. Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số. 3. Nếu hàm số có đạo hàm trên khoảng và đạt cực đại hoặc cực tiểu tại thì . |
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Chiếu hoặc vẽ đồ thị hàm số lên bảng. Yêu cầu học sinh đọc SGK, thảo luận theo nhóm 2 học sinh. HS: Nhận nhiệm vụ từ giáo viên. |
|
Thực hiện |
- HS thảo luận cặp đôi thực hiện nhiệm vụ - GV theo dõi, hỗ trợ , hướng dẫn các nhóm |
|
Báo cáo thảo luận |
GV gọi hai nhóm bất kỳ trình bày kết quả thảo luận. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét và kết luận, củng cố giúp học sinh phát biểu đúng khái niệm và gọi đúng các tên gọi , , . |
2.2. HOẠT ĐỘNG 2.2. ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ
a) Mục tiêu: Học sinh nhận biết được mối liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
b)Nội dung:
GV cho học sinh đọc SGK, thảo luận theo nhóm 2 học sinh và thực hiện các yêu cầu sau:
H1: Trong Hoạt động 2.1 nêu mối liên hệ giữa đạo hàm cấp 1 và những điểm tại đó hàm số có có giá trị lớn nhất?
H2: Nêu mối liên hệ giữa dấu của đạo hàm và sự tồn tại cực đại, cực tiểu của hàm số.
Ví dụ:Tìm cực trị của các hàm số sau :
H3: Nêu quy tắc tìm cực trị của hàm số?
c) Sản phẩm:
|
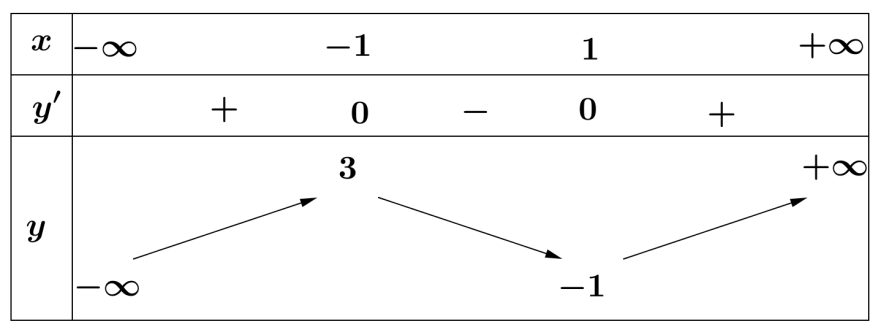
TL1: Các nhóm thảo luận và trả lời: Ta thấy x=1 và x=3 là nghiệm phương trình TL2: ĐỊNH LÍ 1: Giả sử hàm số liên tục trên khoảng và có đạo hàm trên K hoặc trên , với h>0. a) Nếu trên khoảng và trên khoảng thì là một điểm cực đại của hàm số . b) Nếu trên khoảng và trên khoảng thì là một điểm cực tiểu của hàm số . Ví dụ: 1) .
Bảng xét dấu
Kết luận: Hàm số đạt cực đại tại x=-1 và đạt cực tiểu tại x=1. 2) D= R. Bảng xét dấu
Kết luận: Hàm số đạt cực đại tại và đạt cực tiểu tại x=0. 3)
Kết luận:Hàm số không có cực trị TL3:QUY TẮC I: Để tìm cực trị của hàm số ta thực hiện lần lượt các bước sau đây Bước 1: Tìm tập xác định của hàm số. Bước 2: Tìm . Tìm các điểm tại đó bằng 0 hoặc không xác định. Bước 3: Lập bảng biến thiên của hàm số. Bước 4: Từ bảng biến thiên suy ra các điểm cực trị. |
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Yêu cầu học sinh đọc SGK, thảo luận theo nhóm 2 học sinh và trả lời các câu hỏi nêu trên. HS: Nhận nhiệm vụ từ giáo viên. |
|
Thực hiện |
- HS thảo luận cặp đôi thực hiện nhiệm vụ - GV theo dõi, hỗ trợ , hướng dẫn các nhóm |
|
Báo cáo thảo luận |
GV gọi bốn nhóm bất kỳ trình bày kết quả thảo luận. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét, sửa lỗi và củng cố kiến thức cho học sinh. |
2.3. HOẠT ĐỘNG 2.3. QUY TẮC TÌM CỰC TRỊ, ĐỊNH LÍ 2
a) Mục tiêu: Học sinh nhận ra và hiểu được mối liên hệ giữa đạo hàm cấp hai và sự tồn tại cực trị của hàm số.
b)Nội dung:
H1: Cho hàm số
a) Giải phương trình , tìm các nghiệm
b) Tính , và nhận định về dấu của
H2: Nêu mối liên hệ giữa đạo hàm cấp hai và sự tồn tại cực trị của hàm số.
H3: Nêu quy tắc tìm cực trị của hàm số dựa vào dấu của đạo hàm cấp 2.
c) Sản phẩm:
|
TL1: ; ; ; TL2: ĐỊNH LÍ 2: Cho hàm số có đạo hàm cấp hai trong khoảng , với h>0. Khi đó: a) Nếu thì là điểm cực tiểu của hàm số. b) Nếu thì là điểm cực đại của hàm số. TL3: QUY TẮC II: Để tìm điêm cực đại, cực tiểu của hàm số ta thực hiện các bước sau: Bước 1: Tìm tập xác định của hàm số. Bước 2: Tính . Giải phương trình và kí hiệu là các nghiệm của phương trình. Bước 3: Tính và . Bước 4: Dựa vào dấu của suy ra điểm cực trị của hàm số. |
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Yêu cầu học sinh đọc SGK, thảo luận theo nhóm 2 học sinh và trả lời các câu hỏi nêu trên. HS: Nhận nhiệm vụ từ giáo viên. |
|
Thực hiện |
- HS thảo luận cặp đôi thực hiện nhiệm vụ - GV theo dõi, hỗ trợ , hướng dẫn các nhóm |
|
Báo cáo thảo luận |
GV gọi ba nhóm bất kỳ trình bày kết quả thảo luận. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét, sửa lỗi và củng cố kiến thức cho học sinh. |
3. HOẠT ĐỘNG 3: LUYỆN TẬP
Hoạt động 3.1.Áp dụng quy tắc I, hãy tìm cực trị của các hàm số
a) Mục tiêu:
HS biết AD quy tắc I, hãy tìm các điểm cực trị của các hàm số.
b) Nội dung:
Câu a), e) của bài tập 1 trang 18 SGK: Áp dụng Quy tắc I, hãy tìm các điểm cực trị của hàm số:
a) e)
c) Sản phẩm:
Bài giải của học sinh
1a)Lời giải
TXĐ:
BBT
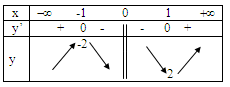
Hàm số đạt cực đại tại x=-1( yCĐ = -2)
Hàm số đạt cực tiểu tại x=1 (yCT = 2)
1e)Lời giải:
+ Vì nên TXĐ của hàm số là
có tập xác định là
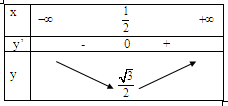
Hàm số đạt cực tiểu tại (yCT =)
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Chia lớp thành 4 nhóm, GV giao nhiệm vụ cho HS nghiên cứu, trao đổi theo từng nhóm. HS: Nhận và thực hiện nhiệm vụ trao đổi theo nhóm |
|
Thực hiện |
GV: điều hành, quan sát các nhóm thực hiện và gợi ý tháo gỡ khó khăn cho HS bằng các câu hỏi dẫn dắt ( nếu cần). HS: Đọc và nghiên cứu đề bài trao đổi theo nhóm tìm hướng giải quyết bài toán |
|
Báo cáo thảo luận |
HS cử đại diện trình bày sản phẩm. Nhận xét bài của bạn. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo |
Hoạt động 3.2.AD quy tắc II, hãy tìm các điểm cực trị của các hàm số
a) Mục tiêu:HS biết AD quy tắc II, hãy tìm các điểm cực trị của các hàm số
b) Nội dung:
Câu b) của bài tập 2 trang 18 SGK: Áp dụng Quy tắc II, hãy tìm các điểm cực trị của hàm số:
c) Sản phẩm:
Bài giải của học sinh.
Lời giải:
TXĐ: R
Hàm số đạt cực đại tại , (yCĐ =)
Hàm số đạt cực tiểu tại , (yCT =)
d) Tổ chức thực hiện :
|
Chuyển giao |
GV: Chia lớp thành 4 nhóm, GV giao nhiệm vụ cho HS nghiên cứu, trao đổi theo từng nhóm. HS: Nhận và thực hiện nhiệm vụ trao đổi theo nhóm |
|
Thực hiện |
GV: điều hành, quan sát các nhóm thực hiện và gợi ý tháo gỡ khó khăn cho HS bằng các câu hỏi dẫn dắt ( nếu cần). HS: Đọc và nghiên cứu đề bài trao đổi theo nhóm tìm hướng giải quyết bài toán |
|
Báo cáo thảo luận |
HS cử đại diện trình bày sản phẩm. Nhận xét bài của bạn. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo |
Hoạt động 3.3. Chứng minh một hàm số bậc 3 có chứa tham số m luôn có 1 cực đại và 1 cực tiểu
a) Mục tiêu:HS biết cách áp dụng định lí 1 để chứng minh hàm số bậc ba luôn có 1 cực đại và 1 cực tiểu.
b) Nội dung:
Bài tập 4 trang 18 SGK:
Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn có 1 cực đại và 1 cực tiểu.
c) Sản phẩm:
Bài giải của học sinh.
Lời giải:
TXĐ: R
Ta thấy có nên phương trình y’ = 0 có hai nghiệm phân biệt và qua hai nghiệm này y’ đổi dấu 2 lần.
Vậy hàm số đã cho luôn có 1 cực đại và 1 cực tiểu với mọi ![]() .
.
d) Tổ chức thực hiện:
|
Chuyển giao |
GV: Chia lớp thành 4 nhóm, GV giao nhiệm vụ cho HS nghiên cứu, trao đổi theo từng nhóm. HS: Nhận và thực hiện nhiệm vụ trao đổi theo nhóm |
|
Thực hiện |
GV: điều hành, quan sát các nhóm thực hiện và gợi ý tháo gỡ khó khăn cho HS bằng các câu hỏi dẫn dắt ( nếu cần). HS: Đọc và nghiên cứu đề bài trao đổi theo nhóm tìm hướng giải quyết bài toán |
|
Báo cáo thảo luận |
HS cử đại diện trình bày sản phẩm. Nhận xét bài của bạn. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo |
Hoạt động 3.4.Xác định giá trị của tham số m để hàm số đạt cực đại tại
a) Mục tiêu:Biết sử dụng định lí 1 hoặc 2 để tìm tham số ![]() sao cho hàm số đạt cực trị tại
sao cho hàm số đạt cực trị tại
b) Nội dung:
Bài tập 6 trang 18 SGK:
Xác định giá trị của tham số m để hàm số đạt cực đại tại x=2.
c) Sản phẩm:
Bài giải của học sinh
Lời giải:
TXĐ:
Hàm số đã cho các đạt cực trị tại
Thử lại:
Với thì
Lập BBT
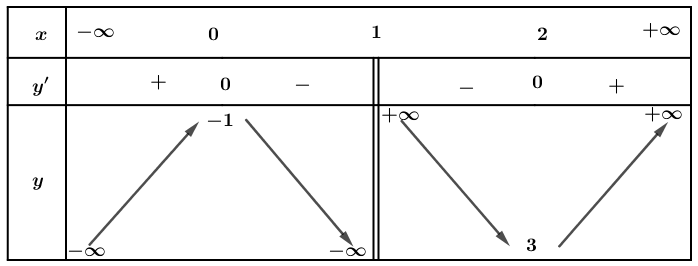
Từ BBT ta thấy hàm số đạt cực tiểu tại x=2 nên m=-1 không phải là giá trị cần tìm.
Với m=-3 thì
Lập BBT
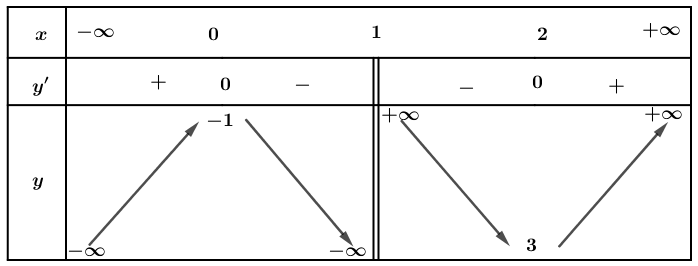
Từ BBT ta thấy hàm số đạt cực đại tại x=2 nên m=-3 là giá trị cần tìm.
Vậy m=-3 là giá trị cần tìm.
d) Tổ chức hoạt động
|
Chuyển giao |
GV: Chia lớp thành 4 nhóm, GV giao nhiệm vụ cho HS nghiên cứu, trao đổi theo từng nhóm. HS: Nhận và thực hiện nhiệm vụ trao đổi theo nhóm |
|
Thực hiện |
GV: điều hành, quan sát các nhóm thực hiện và gợi ý tháo gỡ khó khăn cho HS bằng các câu hỏi dẫn dắt ( nếu cần). HS: Đọc và nghiên cứu đề bài trao đổi theo nhóm tìm hướng giải quyết bài toán |
|
Báo cáo thảo luận |
HS cử đại diện trình bày sản phẩm. Nhận xét bài của bạn. |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. GV chỉ ra sai lầm hay mắc phải( nếu có), khắc sâu cho HS các dạng thường gặp và cách đặt u và dv hợp lí trong từng dạng |
Hoạt động 3.5. Rèn luyện kỹ năng ở kiểu bài trắc nghiệm .
a) Mục tiêu:Giúp HS thực hiện bài tập liên quan đến cực trị ở dạng trắc nghiệm.
b) Nội dung: GV phát phiếu học tập số 1 và yêu cầu học sinh thực hiện các bài tập theo từng cá nhân.
PHIẾU HỌC TẬP 1
Câu 1.[ĐỀ CHÍNH THỨC 2018-2019] Cho hàm số có bảng biến thiên sau:
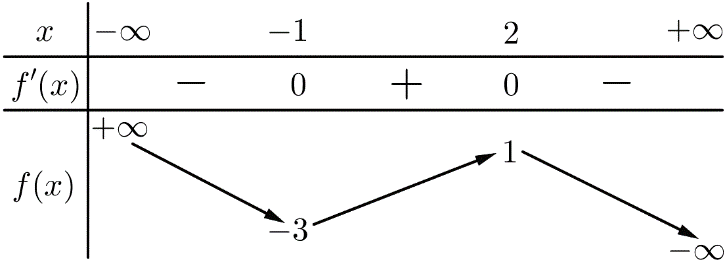
Hàm số đã cho đạt cực tiểu tại điểm
A. x=-3 B. x=-1 C. x=1 D. x=2
Câu 2.[ĐỀ THAM KHẢO 2017-2018]Cho hàm số có bảng biến thiên sau:
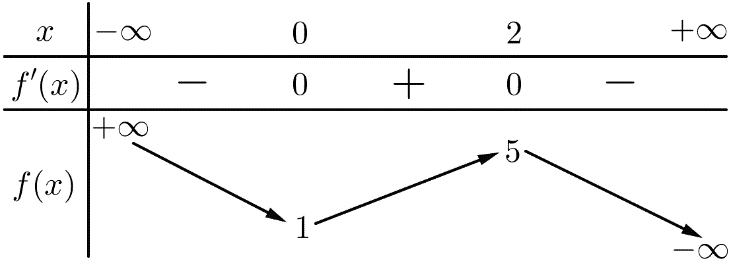
Hàm số đã cho đạt cực đại tại điểm
A. x=0 B. x=1 C. x=2 D. x=5
Câu 3.[ĐỀ CHÍNH THỨC 2016-2017]Cho hàm số có bảng biến thiên sau:
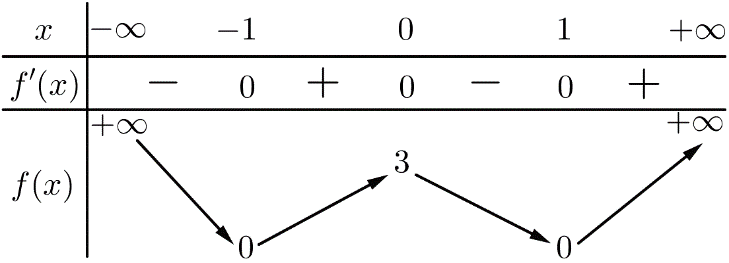
Mệnh đề nào sau đây sai?
A. Hàm số có hai điểm cực tiểu. B. Hàm số có giá trị cực đại bằng 0
C. Hàm số có ba điểm cực trị. D. Hàm số có giá trị cực đại bằng 3
Câu 4. Cho hàm số f(x) liên tục trên R và có bảng xét dấu đạo hàm như sau:
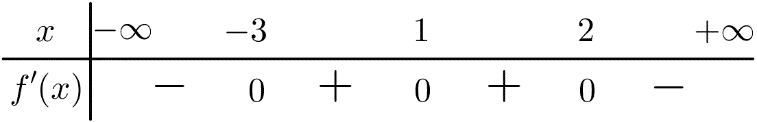
Hỏi hàm số f(x) có bao nhiêu điểm cực trị?
A.0 B.1 C.2 D.3
Câu 5.Tìm các điểm cực trị của hàm số
A. và B. và
C. và D. và
Câu 6.[ĐỀ MINH HỌA 2016-2017]Giá trị cực đại của hàm số bằng
A. -1 B. 0 C. 1 D. 4
Câu 7.[ĐỀ CHÍNH THỨC 2016-2017]Tìm giá trị thực của tham số ![]() để đường thẳng vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
để đường thẳng vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
A. B. C. D.
Câu 8.Tập hợp các giá trị của tham số ![]() để hàm số có hai điểm cực trị là
để hàm số có hai điểm cực trị là
A. B. C. D.
Câu 9. Cho hàm số với m là tham số thực. Tìm tất cả các giá trị của m để hàm số đạt cực tiểu tại điểm x=-1
A. m=1 B. m=-3. C. m=1, m=-3. D.
Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số đạt cực đại tại x=2
A. m=-1 B. m=-3 C. m=-1,m=-3 D. m=3
c) Sản phẩm:
Bài giải chi tiết trên giấy của HS.
Câu 1. Lời giải. Chọn B.
Câu 2.Lời giải. Chọn C.
Câu 3.Lời giải. Chọn B.
Câu 4.Lời giải.Nhận thấy đổi dấu khi qua x=-3 và x=2 nên hàm số có 2 điểm cực trị(x=1 không là điểm cực trị vì không đổi dấu khi qua x=1). Chọn C.
Câu 5. Lời giải.Ta có Chọn D.
Câu 6. Lời giải.Ta có
Bảng biến thiên
Vậy giá trị cực đại của hàm số bằng 4Chọn D.
Cau 7.Lời giải.Xét hàm có
Suy ra là hai điểm cực trị của đồ thị hàm số.
Suy ra đường thẳng AB có một VTCP là VTPT
Đường thẳng có một VTPT là
YCBT Chọn D.
Câu 8. Lời giải. Ta có Để hàm số có hai điểm cực trị có hai nghiệm phân biệt Chọn B.
Câu 9.Lời giải. Đạo hàm: và
Hàm số đạt cực tiểu tại
Thử lại ta thấy chỉ có giá trị m=-3 thỏa mãn (vì đổi dấu từ sang khi qua x=-1).Chọn B.
Câu 10.Lời giải. TXĐ: Đạo hàm:
Hàm số đạt cực đại tại
![]() Thử lại với m=-1 thì hàm số đạt cực tiểu tại x=2 không thỏa mãn.
Thử lại với m=-1 thì hàm số đạt cực tiểu tại x=2 không thỏa mãn.
![]() Thử lại với m=-3 thì hàm số đạt cực đại tại x=2 thỏa mãn. Chọn B.
Thử lại với m=-3 thì hàm số đạt cực đại tại x=2 thỏa mãn. Chọn B.
d) Tổ chức thực hiện:
|
Chuyển giao |
GV: Phát phiếu học tập số 1 cho học sinh làm việc cá nhân đọc lập HS:Nhận phiếu học tập để nghiên cứu |
|
Thực hiện |
GV: Theo dõi,quan sát và gợi ý khi học sinh yêu cầu giúp đỡ HS: Thực hiện theo đúng thời gian quy định |
|
Báo cáo thảo luận |
Học sinh trình bày bài giải. Nhận xét bài của bạn.Nêu câu hỏi để hiểu hơn các vấn đề |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận bài làm của HS,nhận xét, làm rõ vấn đề, chốt kiến thức toàn bài Hướng dẫn HS xây dựng sơ đồ tư duy các kiến thức trong bài học. |
4.HOẠT ĐỘNG 4: VẬN DỤNG
a) Mục tiêu:HS biết vận dụng các kiến thực liên quan để giải một số bài toán
b) Nội dung: GV phát phiếu học tập 2 cho học sinh và yêu cầu thực hiện ở nhà
PHIẾU HỌC TẬP 2
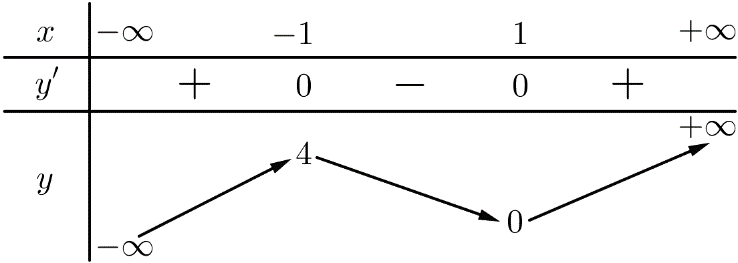
Câu 1.[Đại học Vinh lần 1, năm 2018-2019]Cho hàm số có bảng biến thiên như hình vẽ
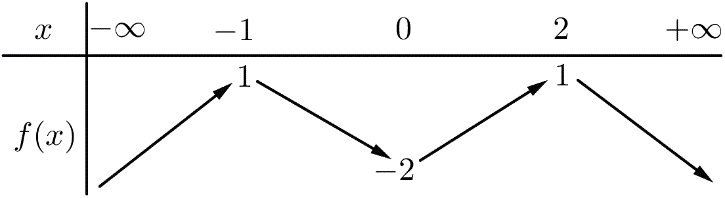
Hàm số đạt cực đại tại
A. x=-2 B. x=-1 C. D. x=1
Câu 2. Cho hàm số xác định, liên tục trên ![]() và có bảng biến thiên sau:
và có bảng biến thiên sau:
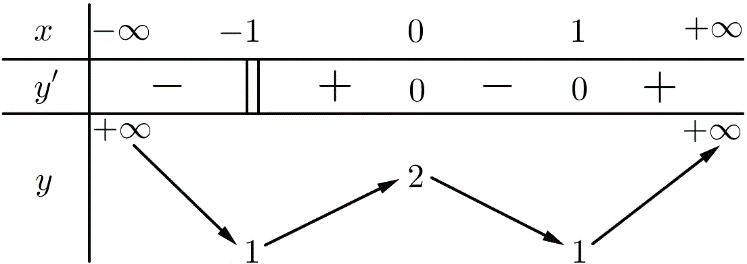
Hàm số đạt cực tiểu tại điểm nào sau đây?
A.x=-1 B.x=1 C. D.x=0
Câu 3.Cho hàm số có bảng biến thiên như sau:
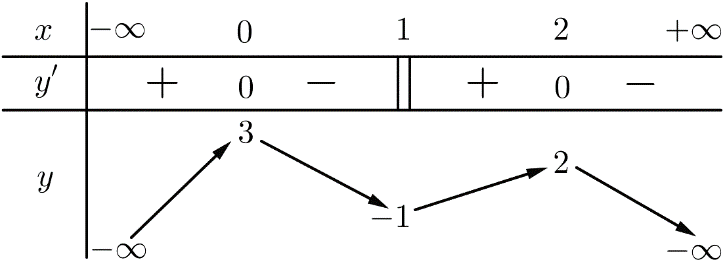
Hàm số có bao nhiêu điểm cực trị?
A. 2 B. 3 C. 5 D. 6
Câu 4. Gọi là hai điểm cực trị của hàm số Tìm các giá trị của tham số m để
A. m=0 B. C. D.
Câu 5. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn để hàm số có hai điểm cực trị nằm trong khoảng ?
A. 2017 B. 2018 C. 2019 D. 2020
Câu 6.Tìm tất cả các giá trị thực của tham số m để khoảng cách từ điểm đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số bằng
A. B.m=-1. C. D. Không tồn tại m
Câu 7. Tìm giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị A,B sao cho tam giác OAB vuông tại O với O là gốc tọa độ.
A. m=-1 B. m=0 C. D. m=1
Câu 8. Tìm tất cả các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị A,B sao cho A,B và thẳng hàng.
A. B. C. D. m=0
c) Sản phẩm:
Bài giải chi tiết trên giấy của HS
Câu 1. Lời giải. Ta có
Bảng biến thiên
Dựa vào BTT, ta thấy hàm số g(x) đạt cực đại tại và tại x=1 Chọn D.
Câu 2.Lời giải. Ta có
Do đó điểm cực tiểu của hàm số trùng với điểm cực tiểu của hàm số
Vậy điểm cực tiểu của hàm số là Chọn C.
Câu 3.Lời giải.Ta có
![]()
![]() g'(x) không xác định
g'(x) không xác định
Bảng biến thiên
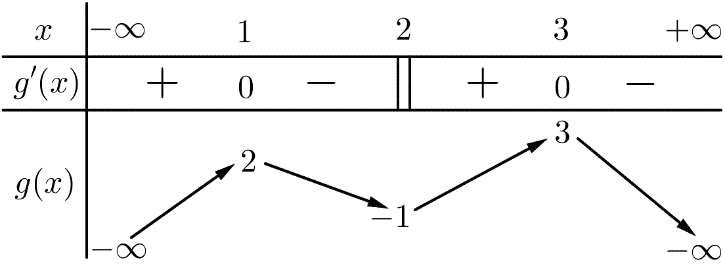
Vậy hàm số có 3 điểm cực trị. Chọn B.
Câu 4.Lời giải. Đạo hàm: Có nên hàm số luôn có hai điểm cực trị Theo định lí Viet, ta có
YCBT Chọn D.
Câu 5.Lời giải. Đạo hàm:
Yêu cầu bài toán có hai nghiệm dương phân biệt
Câu 6. Lời giải.Đạo hàm:
Để hàm số có hai điểm cực trị có hai nghiệm phân biệt . (*)
Thực hiện phép chia y cho y' ta được phần dư Suy ra đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có phương trình
Yêu cầu bài toán Chọn B.
Câu 7.Lời giải.Đạo hàm:
Để hàm số có hai điểm cực trị có hai nghiệm phân biệt
Tọa độ các điểm cực trị của đồ thị hàm số là: và
Yêu cầu bài toán Chọn C.
Câu 8.Lời giải.Đạo hàm:
Nên hàm số có hai điểm cực trị có hai nghiệm phân biệt
Tọa độ các điểm cực trị của đồ thị hàm số là: và
Suy ra
Ba điểm A, B và M thẳng hàng Chọn C.
d) Tổ chức thực hiện
|
Chuyển giao |
GV: Phát phiếu học tập 2 cho HS tùy chọn phương án làm việc ( Cá nhân hoặc nhóm) HS:Nhận phiếu học tập để nghiên cứu |
|
Thực hiện |
GV: Cho học sinh làm ngoài giờ học chính khóa HS: Thực hiện tại nhà theo đúng thời gian quy định |
|
Báo cáo thảo luận |
Nộp bài làm vào tiết học tuần sau |
|
Đánh giá, nhận xét, tổng hợp |
GV nhận bài làm của HS, nhận xét, làm rõ vấn đề, chốt kiến thức toàn bài Hướng dẫn HS xây dựng sơ đồ tư duy các kiến thức trong bài học |
Ngày ...... tháng ....... năm 2021
BCM ký duyệt
Xem thêm các bài Giáo án Toán lớp 12 hay, chi tiết khác:
Giáo án Sự đồng biến, nghịch biến của hàm số
Giáo án Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12