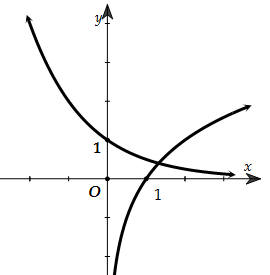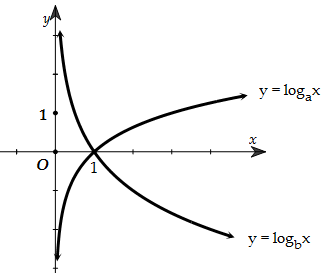Giáo án Bài tập ôn tập chương 2 mới nhất - Toán 12
Với Giáo án Bài tập ôn tập chương 2 mới nhất Toán lớp 12 được biên soạn bám sát sách Toán 12 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 12 Bài tập ôn tập chương 2
|
Trường:…………………………….. Tổ:TOÁN Ngày soạn: …../…../2021 Tiết: |
Họ và tên giáo viên: …………………………… Ngày dạy đầu tiên:…………………………….. |
Môn học/ Hoạt động giáo dục: Toán – GT: 12
Thời gian thực hiện: ….. tiết
I. MỤC TIÊU
1. Về kiến thức
- Sau khi học xong bài này học sinh nhớ lại và nắm vững được về các kiến thức sau:
- Tính chất của luỹ thừa với số mũ thực
- Tính chất của hàm số luỹ thừa
- Tính chất của hàm số mũ và hàm số Lôgarit
- Dạng và cách giải phương trình, bất pt mũ và logarit
2. Về năng lực
2.1. Năng lực chung: Thực hiện bài học này sẽ góp phần củng cố và hệ thống lại một số năng lực sau của học sinh:
- Năng lực tự chủ và tự học: Tìm kiếm thông tin, đọc sách giáo khoa, tìm kiếm các bài tập trên mạng internet
- Năng lực giao tiếp và hợp tác: Thảo luận nhóm để hoàn thành bài tập
- Năng lực giải quyết vấn đề và sáng tạo: vận dụng kiến thức về hàm số mũ và lũy thừa để giải quyết một số bài toán thực tế.
2.2 Năng lực Toán học
- Nắm được cách tìm TXĐ hàm luỹ thừa và hàm Logarit
- Vận dụng linh hoạt các công thức luỹ thừa, lôgarit
- Giải các phương trình và bpt mũ và logarit một cách thành thạo
- Thực hiện thành thạo các bài tập dạng trắc nghiệm
3. Về phẩm chất
Học sinh phát triển phẩm chất nhân ái, trung thực, có cách đánh giá đúng đắn khách quan đến bài làm của các bạn và các nhóm khác.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Giáo viên
- Dụng cụ dạy học, máy vi tính, máy chiếu.
- Các phiếu học tập về tính chất của lũy thừa, hàm số lũy thừa, hà số mũ, hàm số logarit.
- Phiếu câu hỏi trắc nghiệm về toàn bộ nội dung trong chương 2 để học sinh luyện tập.
2. Học sinh
- Đồ dùng học tập, bài cũ là lí thuyết và các dạng bài tập đã học trong toàn chương 2
III. TIẾN TRÌNH TỔ CHỨC HOẠT ĐỘNG DẠY VÀ HỌC
1. HOẠT ĐỘNG 1: KHỞI ĐỘNG
a. Mục tiêu: Để học sinh ôn lại các phần kiến thức lý thuyết đã học trong chương 2: Luỹ thừa, Hàm số luỹ thừa, Lôgarit, Hàm số mũ, Hàm số lôgarit
b. Nội dung: Giáo viên đưa các phiếu bài tập theo nhóm để học sinh hoàn thành các phiếu bài tập đó. Phiếu bài tập dưới dạng yêu cầu là giáo viên để bỏ ngỏ công thức và lý thuyết sau đó học sinh sẽ bổ sung công thức và lý thuyết
c. Sản phẩm: Phiếu học tập đã hoàn thiện, bao gồm các công thức và lý thuyết về lũy thừa, hàm số lũy thừa, hàm số mũ, hàm số lgarit.
d. Tổ chức thực hiện
c.1. Tiếp cận
*Chuyển giao nhiệm vụ:
Giáo viên chia lớp thành 4 nhóm. Mỗi nhóm hoàn thành một phiếu học tập
Yêu cầu học sinh hãy điền vào phần còn thiếu trong dấu ………….trong các phiếu học tập sau
Yêu cầu các nhóm trình bày kết quả sau khi thảo luận
- NHÓM 1: PHIẾU HỌC TẬP SỐ 1
|
PHIẾU HỌC TẬP 1: Cho a,b là những số thực dương; α,β là những số thực tuỳ ý. Khi đó ta có: aα.aβ=..........;aαaβ=............;..........=aα.β;(ab)α=...........;............=aαbα;
Nếu a>1 thì aα>aβ khi và chỉ khi …………………. Nếu a<1 thì aα<aβ khi và chỉ khi …………………. |
- NHÓM 2: PHIẾU HỌC TẬP SỐ 2
|
PHIẾU HỌC TẬP 2: Hãy hoàn thành bảng tóm tắt tính chất của hàm số luỹ thừa y=xα trên khoảng (0;+∞) dưới đây
|
- NHÓM 3: PHIẾU HỌC TẬP SỐ 3
|
PHIẾU HỌC TẬP 3: Hãy hoàn thành bảng tóm tắt tính chất của hàm số mũ y=ax(a>0,a≠1) dưới đây
|
- NHÓM 4: PHIẾU HỌC TẬP SỐ 4
|
PHIẾU HỌC TẬP 4: Hãy hoàn thành bảng tóm tắt tính chất của hàm số lôgarit y=logax(a>0,a≠1) dưới đây
|
c.2 Thực hiện nhiệm vụ:Học sinh thực hiện cá nhân và theo nhóm
c.3 Báo cáo nhiệm vụ: Đại diện 4 nhóm trình bày. Các nhóm khác cử đại diện phản biện
c.4 Đánh giá nhận xét tổng hợp: Giáo viên chốt lại kết quả chính xác
d.Củng cố kiến thức: Qua đây các e cần phải ghi nhớ các tình chất luỹ thừa với số mũ thực, tính chất của hàm số luỹ thừa, hàm số mũ, hàm số lôgarit
2. HOẠT ĐỘNG 2: LUYỆN TẬP
a) Mục tiêu: - HS hiểu và biết liên kết các tính chất của đồ thị vào nhận dạng các yếu tố của hàm số mũ, hàm số loga.
- Biết giải một só phương trình, bất phương trình mũ và logarit thường gặp.
- Vận dụng được kiến thức về giải phương trinh, bất phương trình mũ và logarit vào tìm tham số thỏa điều kiện bài toán.
b) Nội dung: Nêu ND bài tập / Phiếu học tập.
PHIẾU HỌC TẬP SỐ 1 – (LUYỆN TẬP NHẬN DẠNG ĐỒ THỊ HÀM SỐ)
|
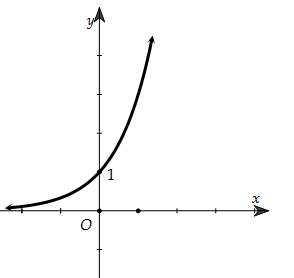
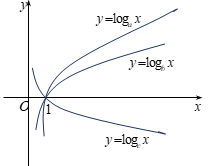
Câu 1. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây ? C.y=log3x. D.y=−log3x.
|
|
|
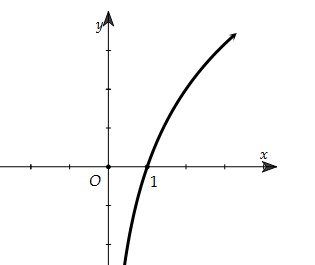
Câu 2. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây ? A.y=ex. B.y=e−x. C.y=log√2x. D.y=logπ4x.
|
|
|
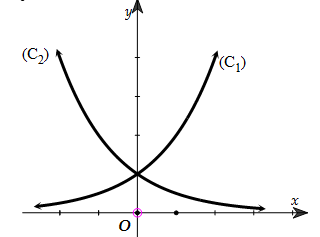
Câu 3. Cho hai hàm số y=ax,y=bx với a,b là hai số thực dương khác 1 lần lượt có đồ thị là (C1) và (C2) như hình bên. Mệnh đề nào dưới đây đúng? A.0<a<b<1. B.0<b<1<a. C.0<a<1<b. D.0<b<a<1. |
|
|
Câu 4. Cho đồ thị hàm số y=ax,y=logbx như hình vẽ bên. Mệnh đề nào dưới đây đúng? A.0<a<1<b. B.0<b<1<a. C.0<a<b<1. D.1<b<a. |
|
|
Câu 5. Cho hàm số y=logax và y=logbx có đồ thị như hình vẽ bên. Trong các kết luận dưới đây, đâu là kết luận đúng? A.0<a<1<b. B.0<b<a<1. C.0<a<b<1. D.0<b<1<a. |
|
|
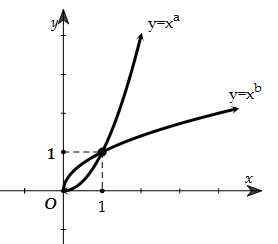
Câu 6. Cho a,b là các số thực. Đồ thị các hàm số y=xa,y=xb trên khoảng (0;+∞) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng? A.0<b<1<a. B.b<0<1<a. C.0<a<1<b. D.0<a<1<b. |
|
|
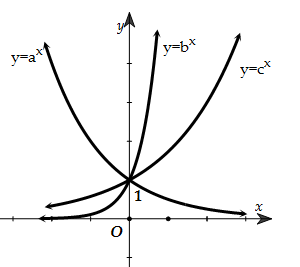
Câu 7. Cho a,b,c các số dương khác 1. Đồ thị các hàm số y=ax,y=bx,y=cx được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng? A.a<b<c B.a<c<b C.b<c<a D.c<a<b |
|
Câu 8. Cho a,b,c các số dương khác 1. Đồ thị y=logax , y=logbx , y=logcx được cho ở hình bên. Khẳng định nào sau đây đúng?
A.0<a<b<1<c .
B.0<c<1<a<b .
C.0<c<a<1<b .
D. 0<c<1<b<a
 .
.
|
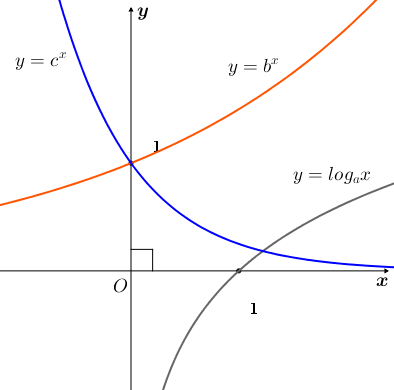
Câu 9. Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số y=logax ,y=bx , y=cx được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng? A. c<a<b B.b<c<a C.a<b<c D.c<b<a |
|
|
Câu 10. Cho các hàm số y=logax và y=logbx có đồ thị như hình vẽ bên. Đường thẳng x=7 cắt trục hoành, đồ thị hàm số y=logax và y=logbx lần lượt tại H, M, N. Biết rằng HM=MN . Mệnh đề nào sau đây là đúng? A.a=7b . B.a=2b . C.a=b7 . D.a=b2 . |
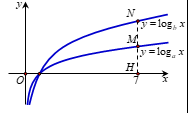
|
PHIẾU HỌC TẬP SỐ 2 – (LUYỆN TẬP TÌM NGHIỆM PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH)
Câu 1. Tìm nghiệm của phương trình 32x−1=243
A.x=9 B.x=3 C.x=4 D.x=10
Câu 2. Tổng các nghiệm của phương trình 9x−4.3x+3=0 bằng
A.1 B.4 C.-1 D.-2
Câu 3. Phương trình 3.9x−7.6x+2.4x=0 có hai nghiệm x1, x2. Tổng x1+x2 bằng
A.1 B.-1 C.log3273⋅ D.73
Câu 4. Bất phương trình 5x+1>125 có nghiệm là
A.x>32 B.x>52 C.x>1 D.x>2
Câu 5. Bất phương trình log4(x−1)=3. có nghiệm là
A.x≤4. B.x≥1. C.x≤3. D.x≤2
Câu 6. Tìm nghiệm của phương trình log4(x−1)=3.
A.x=63 B.x=65 C.x=80 D.x=82
Câu 7. Tìm số nghiệm của phương trình .
A. . B. . C. . D. .
Câu 8.Phương trình 2(log3x)2−5log3(9x)+3=0 có tích các nghiệm là:
A.27√5 B. 7 C.27√3 D.27√3
Câu 9 .Tìm nghiệm của bất phương trình log2(1−x)>2 .
A.x<−3 . B.x<−4 . C.x<3 . D.x<5 .
Câu 10. Cho bất phương trình log0,2x−log5(x−2)<log0,23 . Nghiệm của bất phương trình đã cho là
A.2<x<3 . B.2≤x<3 . C.x<−1 hoặc x>3 .
D.x>3 .
PHIẾU HỌC TẬP SỐ 3 – ( LUYỆN TẬP TÌM THAM SỐ THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC)
Câu 1. Tìm tất cả các giá trị thực của tham số m để phương trình log24x+3log4x+2m−1=0 có 2 nghiệm phân biệt?
A. . B. . C. . D. .
Câu 2. Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình. logm(2x2+x+3)≤logm(3x2−x). Biết rằng x=1 là một nghiệm của bất phương trình.
A.S=(−2;0)∪(13; 3] . B.S=(−1;0)∪(13; 2 ] .
C.S=[−1;0)∪(13; 3] . D.S=(−1;0)∪(1; 3 ] .
Câu 3. Tìm tất cả các giá trị thực của tham số m để phương trình log23x−(m+2)log3x+3m−1=0 có hai nghiệm x1,x2 thỏa mãn x1.x2=27. ?
A.m=−2 . B.m=-1 . C.m=1 . D.m=2 .
Câu 4. Tìm tất cả tham số m để phương trình log2x+mlogx+m+3=0 có nghiệm x>1
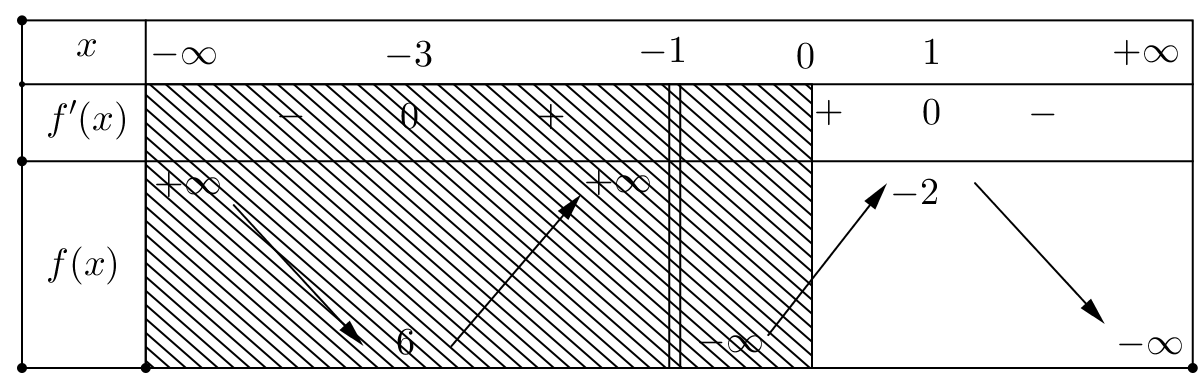
A.m≤−2 B.−3<m≤−2 C.m<−3
D.m≥6
c) Sản phẩm:
PHIẾU HỌC TẬP SỐ 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
C |
C |
A |
D |
B |
B |
B |
D |
D |
PHIẾU HỌC TẬP SỐ 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
A |
B |
D |
A |
B |
B |
D |
A |
D |
PHIẾU HỌC TẬP SỐ 3
|
1A |
Đặt t=log4x Phương trình log24x+3log4x+2m−1=0 có hai nghiệm phân biệt khi phương t2+3t+2m−1=0 có 2 nghiệm phân biệt. ⇔Δ=9−4(2m−1)>0⇔m<138. |
|
2C |
Do x=1 là một nghiệm của bất phương trình nên: logm6≤logm2⇒m<1. Suy ra logm(2x2+x+3)≤logm(3x2−x)⇔{2x2+x+3≥3x2−x3x2−x>0 ⇔{−1≤x≤3x<0∨x>13⇔−1≤x<0∨13<x≤3
|
|
3C |
Đặt t=log3x suy ra x1=3t1;x2=3t2. Do x1.x2=27⇒3t1.3t2=27⇒t1+t2=3 . Để phương trình log23x−(m+2)log3x+3m−1=0 có hai nghiệm x1,x2 thỏa mãn x1.x2=27 thì phương trình t2−(m+2)t+3m−1=0 có hai nghiệm t1,t2 thỏa t1+t2=3 Theo Vỉ-et .t1+t2=m+2=3⇒m=1 Thử lại ta thấy m=1 thỏa điều kiện. |
|
4A |
Đặt t=logx , do x>1⇒t>0 Để phương trình log2x+mlogx+m+3=0 có nghiệm x>1 thì phương trình t2+mt+m+3=0 có nghiệm t>0 ⇔m=−t2−3t+1=f(t) với t>0 Hàm số f(t) có bảng biến thiên sau:
Để m=f(t) có nghiệm t>0 thì m≤−2. |
d) Tổ chức thực hiện
|
Chuyển giao
|
GV: Chia lớp thành 4 nhóm, tổ chức, giao nhiệm vụ HS:Nhận |
|
Thực hiện |
GV: điều hành, quan sát, hướng dẫn HS: Đọc, nghe, nhìn, làm ( cách thức thực hiện: cá nhân/cặp/nhóm) |
|
Báo cáo thảo luận |
HS báo cáo, theo dõi, nhận xét /hình thức báo cáo |
|
Đánh giá, nhận xét, tổng hợp
|
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo |
3.HOẠT ĐỘNG 3: VẬN DỤNG.
a) Mục tiêu: Vận dụng các kiến thức về phương trình, bất phương trình mũ và logarít để giải các bài toán liên quan thực tế..
b) Nội dung: Nêu ND bài tập / Phiếu học tập / Yêu cầu thực tế cần tìm hiểu/ nghiên cứu/ trảinghiệm.
PHIẾU HỌC TẬP SỐ 4 – (LUYỆN TẬP ỨNG DỤNG THỰC TIỄN)
Câu 1. Một người gửi tiết kiệm vào ngân hàng khoảng tiền cố định với lãi suất 0.6%/tháng và lãi suất hàng tháng được nhập vào vốn. Hỏi sau bao lâu thì người đó thu được số tiền gấp hơn ba số tiền ban đầu?
A. 184 tháng B. 183 tháng C. 186 tháng D. 185 tháng
Câu 2. Anh Bình vay ngân hàng 2 tỷ đồng để xây nhà và trả dần mỗi năm 500 triệu đồng. Kỳ trả đầu tiên là sau khi nhận vốn với lãi suất trả chậm 9% một năm. Hỏi sau mấy năm anh Bình mới trả hết nợ đã vay?
A.5 . B.3 . C.4 . D.6 .
Câu 3. Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức quảng cáo trên truyền hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau x quảng cáo được phát thì số % người xem mua sản phẩm là P(x)=1001+49e−0.015x,x≥0 . Hãy tính số quảng cáo được phát tối thiểu để số người mua đạt hơn 75%.
A. 343 B. 333 C. 330 D. 323
Câu 4. Năm 2020, tỉ lệ thể tích khí CO2 trong không khí là 397.10−6 . Biết rằng tỉ lệ thể tích khí CO2 trong không khí tăng 0,4% hàng năm. Đến ít nhất bao nhiêu năm thì tỉ lệ thể tích khí CO2 trong không khí vượt ngưỡng 41.10−5?
A. 7 năm. B. 8 năm.
C. 9 năm. D. 10 năm.
Câu 5. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức: m(t)=m0(12)tT , trong đó m0 là khối lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cabon 14C là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng Cabon và xác định được nó đã mất khoảng 25% lượng Cabon ban đầu của nó. Hỏi mẫu đồ cổ đó có tuổi là bao nhiêu?
A. 2400 năm B. 2300 năm C. 2387 năm D. 2378 năm
c) Sản phẩm: Sản phẩm trình bày của cá nhân/ nhóm học sinh
PHIẾU HỌC TẬP SỐ 4.

d) Tổ chức thực hiện
|
Chuyển giao
|
GV: tổ chức, giao nhiệm vụ HS:Nhận |
|
Thực hiện |
GV: điều hành, quan sát, hướng dẫn HS chuẩn bị HS: Đọc, nghe, nhìn, làm ( cách thức thực hiện: cá nhân/cặp/nhóm) Có thể thực hiện tại lớp / ở nhà |
|
Báo cáo thảo luận |
HS báo cáo, theo dõi, nhận xét / hình thức báo cáo |
|
Đánh giá, nhận xét, tổng hợp |
GV nx, làm rõ vấn đề, chốt kiến thức toàn bài Hướng dẫn HS xây dựng sơ đồ tư duy các kiến thức trong bài học |
Ngày ...... tháng ....... năm 2021
TTCM ký duyệt
Xem thêm các bài Giáo án Toán lớp 12 hay, chi tiết khác:
Giáo án Hàm số mũ. Hàm số lôgarit
Giáo án Phương trình mũ và phương trình lôgarit
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12