Giải Toán 6 Bài tập cuối chương 1 - Chân trời sáng tạo
Lời giải bài tập Toán lớp 6 Bài tập cuối chương 1 sách Chân trời sáng tạo với cuộc sống hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6.
Giải Toán 6 Bài tập cuối chương 1
A. Câu hỏi trắc nghiệm
Gọi X là tập hợp các chữ cái trong từ “thanh”. Cách viết đúng là:
Lời giải:
Các chữ cái xuất hiện trong từ “thanh” là: t, h, a, n, h.
Vì các phần tử trong tập hợp chỉ xuất hiện một lần .
Suy ra X = {t, h, a, n}.
Đáp án cần chọn là C.
Gọi X là tập hợp các số tự nhiên không lớn hơn 5. Cách viết sai là:
Lời giải:
Các số tự nhiện không lớn hơn 5, tức là nhỏ hơn hoặc bằng 5, đó là các số 0, 1, 2, 3, 4, 5.
Khi đó ta viết tập hợp X theo cách liệt kê các phần tử là:
X = {0; 1; 2; 3; 4; 5} hoặc X = {0; 2; 4; 1; 3; 5} (thứ tự liên kê không ảnh hưởng)
Do đó A và B là đúng.
Viết tập hợp X theo cách chỉ ra tính chất đặc trưng: X={x∈ℕ|x≤5}. Do đó D đúng, C sai.
Đáp án cần chọn là C.
Lời giải:
(A) a + b = b + a là tính chất giao hoán của phép cộng nên A đúng.
(B) ab = ba là tính chất giao hoán của phép nhân nên B đúng.
(C) ab + ac = a(b + c) là tính chất phân phối của phép cộng với phép nhân nên C đúng.
(D) Ta có: ab – ac = a(b – c) a(c – b) do đó D sai.
Đáp án cần chọn là D.
Toán lớp 6 trang 46 Câu 4
Nhẩm xem kết quả phép tính nào dưới đây là đúng:
Lời giải:
(A) Ta có 11 . 12 = 132 nên A sai.
(B) Ta có 13.99 = 1 287 nên B sai.
(C) Ta có 14.99 = 1 386 nên C đúng.
(D) Ta có 45.9 = 405 nên D sai.
Đáp án cần chọn là C.
Lời giải:
ƯCLN(18, 24) = 2.3 = 6.
Đáp án cần chọn là D.
Lời giải:
3=3; 4=22; 6=2.3
⇒BCNN(3, 4, 6)=22.3=12
B. Bài tập tự luận
Tính giá trị của biểu thức (bằng cách hợp lý nếu có thể).
Lời giải:
a) A = 37.173 + 62.173 + 173
= 37.173 + 62.173 + 173 . 1
= 173.(37 + 62 + 1)
= 173. 100
= 17 300.
b) B = 72.99 + 28.99 – 900
= 99(72 + 28) – 900
= 99.100 – 900
= 9 900 – 900
= 9 000.
c) C=23.3−(110+15):42
=23.3−(110+15):42=8.3−(1+15):16=24−16:16=24−1=23.
d) D=62:4.3+2.52−2010.
=62:4.3+2.52−2010=36:4.3+2.25−1=9.3+50−1=27+50−1=77−1=76.
a) ¯12x02y chia hết cho 2; 3 và cả 5.
b) ¯413x2y chia hết cho 5 và 9 mà không chia hết cho 2.
Lời giải:
a) Để ¯12x02y chia hết cho 2 ⇒y∈{0; 2; 4; 6; 8}
Và ¯12x02y chia hết cho 5 ⇒y∈{0; 5}
Do đó y = 0.
Tổng các chữ số của số đã cho là: 1 + 2 + x + 0 + 2 + y = 5 + x.
Để số chia hết cho 3 thì 5+x⋮3⇒5+x∈B(3)
Mà 0≤x≤9,x∈ℕ⇒x∈{1;4;7}
Vậy với x∈{1;4;7} và y = 0 thì ¯12x02y chia hết cho 2; 3 và cả 5.
b) Để ¯413x2y không chia hết cho 2 ⇒y∉{0; 2; 4; 6; 8}
Và ¯413x2y chia hết cho 5 ⇒y∈{0; 5}
Do đó y = 5.
Tổng các chữ số của số đã cho là: 4 + 1 + 3 + x + 2 + y = 4 + 1 + 3 + x + 2 + 5 = 15 + x.
Để ¯413x2y chia hết cho 9 ⇒15+x⋮9⇒15+x∈B(9)
Mà 0≤x≤9,x∈ℕ⇒x∈{3}
Vậy với và y = 5 thì ¯413x2y chia hết cho 5 và 9 mà không chia hết cho 2.
Viết các tập hợp sau bằng cách liệt kê các phần tử:
a) A = {a ∈ ℕ | 84⋮a; 180⋮a và a > 6}
b) B = {b ∈ ℕ | b ⋮ 12, b ⋮ 15, b ⋮ 18 và 0 < b < 300}
Lời giải:
a) Ta có
Suy ra a∈ƯC(84, 180)
Ta có: 84=22.3.7; 180=22.32.5
Suy ra ƯCLN(84, 180) = 22.3=12
ƯC(84, 180) = Ư(12) = {1; 2; 3; 4; 6; 12}
Mà a > 6 nên a = 12.
Vậy A = {12}.
b) Vì b ⋮ 12, b ⋮ 15, b ⋮ 18 nên b ∈ BC(12, 15, 18)
Ta có: 12=22.3; 15=3.5; 18=2.32
Suy ra BCNN(12, 15, 18) =22.32.5=180
B(180) = {0; 180; 360; 540; …}.
Khi đó BC(12, 15, 18) = B(180) = {0; 180; 360; 540; …}.
Mà 0 < b < 300 nên b = 180.
Vậy B = {180}.
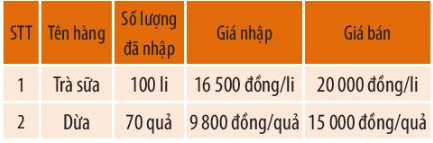
Hỏi lớp 6A đã thu được bao nhiêu tiền lãi? Lớp 6A có hoàn thành mục tiêu đã đề ra không?
Lời giải:
Số tiền lớp 6A bỏ ra để nhập hàng là:
100 . 16 500 + 70 . 9 800 = 2 336 000 (đồng)
Số tiền lớp 6A bán được là:
93.20 000 + 64.15 000 = 2 820 000 (đồng)
Số tiền lãi lớp 6A thu được là:
2 820 000 - 2 336 000 = 484 000 (đồng) < 500 000 (đồng)
Vậy: Với mục tiêu số tiền lãi thu được là 500 000 đồng thì lớp 6A không hoàn thành mục tiêu đã đề ra.
Hãy cho biết số tế bào con có được sau lần phân chia thứ tư, thứ năm, thứ sáu từ một tế bào ban đầu.
Lời giải:
Lần 1: Phân chia thành 2 tế bào con
Lần 2: Phân chia thành 4 tế bào con. Suy ra 4 = 22
Lần 3: Phân chia thành 8 tế bào con. Suy ra 8 = 23
Ta nhận thấy các tế bào phân chia theo lũy thừa của cơ số 2.
Vậy:
Số tế bào con có được sau lần phân chia thứ tư là: 24 = 16 tế bào.
Số tế bào con có được sau lần phân chia thứ năm là: 25 = 32 tế bào.
Số tế bào con có được sau lần phân chia thứ sáu là: 26 = 64 tế bào.
Lời giải:
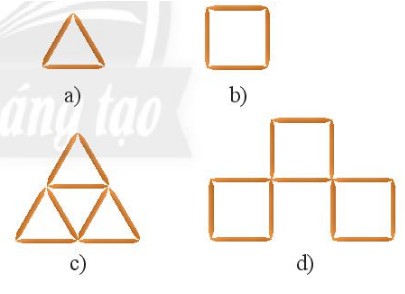
a) Ở trường hợp a, Huy dùng 3 que tăm để xếp được 1 hình.
Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 3 = 12 hình.
b) Ở trường hợp b, Huy dùng 4 que tăm để xếp được 1 hình.
Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 4 = 9 hình.
c) Ở trường hợp c, Huy dùng 9 que tăm để xếp được 1 hình.
Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 9 = 4 hình.
d) Ở trường hợp d, Huy dùng 12 que tăm để xếp được 1 hình.
Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 12 = 3 hình.
a) Hoàn thiện bảng sau vào vở.
ƯCLN(a, b) . BCNN(a, b) và tích a . b
Lời giải:
a)
+) Ta có: 8=23, 10=2.5
⇒ ƯCLN(8, 10) = 2
⇒BCNN(8,10)=23.5=40
+) 24=23.3, 28=22.7
⇒ƯCLN(24, 28) = 22=4
⇒BCNN(24,28)=23.3.7=168
+) 140=22.5.7; 60=22.3.5
⇒ƯCLN(140, 60) = 22.5=20
⇒BCNN(140,60)=22.3.5.7=420
Ta hoàn thiện bảng sau:
|
a |
8 |
24 |
140 |
|
b |
10 |
28 |
60 |
|
ƯCLN(a, b) |
2 |
4 |
20 |
|
BCNN(a, b) |
40 |
168 |
420 |
|
ƯCLN(a,b) . BCNN(a, b) |
80 |
672 |
8 400 |
|
a.b |
80 |
672 |
8 400 |
b) Dựa vào bảng vừa hoàn thành ta có nhận xét sau:
ƯCLN(a, b) . BCNN(a, b) = a . b
Lời giải:
Số lượng túi quà nhiều nhất mà nhóm các bạn có thể chia được là ước chung lớn nhất của 48, 32 và 56.
Ta có: 48=24.3; 32=25; 56=23.7
ƯCLN(48, 32, 56) = 23=8
Vậy số lượng túi quà nhiều nhất mà nhóm có thể chia được là 8 túi.
Khi đó, số lượng vở trong mỗi túi là 48:8 = 6 quyển;
Số lượng thước kẻ trong mỗi túi là 32:8 = 4 cái;
Số lượng bút chì trong mỗi túi là: 56:8 = 7 cái.
Phố phường đông đúc, đèn lồng sao sa
Quẩn quanh, quanh quẩn biết là ai hay
Bảy đèn kết lại còn hai ngọn thừa
Đèn hoa bao ngọn mà ngơ ngẩn lòng.
(Cho biết số đèn từ 600 đến 700 chiếc).
Lời giải:
Phát biểu lại bài toán: Tìm một số từ 600 đến 700 chiếc sao cho số đó chia hết cho 5, chia bảy dư 2 và chia 9 dư 4.
Cộng thêm 5 vào số đó thì số đó chia hết cho 5, 7, 9. Nghĩa là số đó cộng thêm 5 sẽ là bội của 5, 7, 9.
Phân tích 5, 7 và 9 ra thừa số nguyên tố, ta được: 5 = 5, 7 = 7, 9 = 32.
BCNN(5, 7, 9) = 5.7.32 = 315.
BC(5, 7, 9) = B(315) = {0; 315; 630; 945; …}.
Mà số đó nằm trong khoảng từ 600 đến 700 nên số đó là 630.
Vậy số đèn là 630 cái.
Lý thuyết Toán 6 Ôn tập Chương 1 - Chân trời sáng tạo
1. Tập hợp, phần tử
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Mối quan hệ giữa tập hợp và phần tử: Tập hợp chứa phần tử (nếu có) và phần tử nằm trong tập hợp.
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
2. Các kí hiệu tập hợp
- Người ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D, ... và sử dụng các chữ cái thường a, b, c, ... để kí hiệu cho phần tử.
- Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu chấm phẩy dấu “;”. Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
- Phần tử x thuộc tập hợp A được kí hiệu là x ∈ A, đọc là “x thuộc A”. Phần tử y không thuộc tập hợp A được kí hiệu là y ∉ A, đọc là “y không thuộc A”.
3. Các cách cho một tập hợp
Nhận xét. Để cho một tập hợp, thường có hai cách:
• Liệt kê các phần tử của tập hợp.
• Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ngoài 2 cách cho tập hợp như trên, người ta còn minh họa bằng hình vẽ (Sơ đồ Venn).
4. Tập rỗng
Tập rỗng là tập hợp không có phần tử nào, kí hiệu ∅.
5. Tập hợp N và N*
Các số 0; 1; 2; 3; 4; ... là các số tự nhiên.
Tập hợp các số tự nhiên được kí hiệu là N , tức là N = {0; 1; 2; 3; ...}.
Tập hợp các số tự nhiên khác 0 được kí hiệu là N*, tức là N* = {1; 2; 3; ...}
Tập hợp N bỏ đi số 0 thì được N*.
Khi cho một số tự nhiên x ∈N* thì ta hiểu x là số tự nhiên khác 0.
6. Thứ tự trong tập hợp số tự nhiên
a) Biểu diễn các số tự nhiên trên tia số:
Các số tự nhiên được biểu diễn trên tia số bởi các điểm cách đều như sau:
- Tia số có mũi tên sang phải biểu thị chiều tăng dần của các số tự nhiên.
- Mỗi số tự nhiên được biểu diễn bằng một điểm trên tia số; điểm biểu diễn số tự nhiên n được gọi là điểm n.
- Điểm 0 được gọi là gốc.
b) So sánh hai số tự nhiên
- Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết a < b (đọc là a nhỏ hơn b) hoặc b > a (đọc là b lớn hơn a).
- Khi biểu diễn trên tia số nằm ngang có chiều từ trái sang phải, nếu a < b thì điểm a nằm bên trái điểm b.
Ngoài ra ta cũng viết a ≥ b để chỉ a > b hoặc a = b.
+ Nếu a < b và b < c thì a < c (Tính chất bắc cầu).
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.
+ Số 0 là số tự nhiên bé nhất.
7. Ghi số tự nhiên
a) Cách ghi số tự nhiên trong hệ thập phân
Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.
Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó.
Chú ý: Khi viết các số tự nhiên, ta quy ước:
- Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.
- Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.
- Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau.
b) Hệ thập phân
Ta đã biết cấu tạo thập phân của một số:
- Kí hiệu 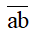
Ta có: 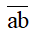
- Kí hiệu 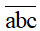
Ta có: 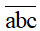
- Với các số cụ thể thì không viết dấu gạch ngang ở trên.
c) Hệ La Mã
Cách ghi số La Mã như sau:
|
Chữ số |
I |
V |
X |
|
Giá trị tương ứng trong hệ thập phân |
1 |
5 |
10 |
Ghép các chữ số I, V, X với nhau ta có thể được số mới. Dưới đây là bảng chuyển đổi La Mã sang số trong hệ thập phân tương ứng (từ 1 đến 10):
|
Số La Mã |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
Giá trị tương ứng trong hệ thập phân |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X
|
XI |
XII |
XIII |
XIV |
XV |
XVI |
XVII |
XVIII |
XIX |
XX |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Các số La Mã biểu diễn các số từ 21 đến 30: Thêm XX vào bên trái mỗi số từ I đến X
Chú ý:
- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.
- Không có số La Mã nào biểu diễn số 0.
8. Phép cộng và phép nhân
Phép cộng (+) và phép nhân (×) các số tự nhiên đã được biết đến ở tiểu học.
Chú ý: Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số ta có thể không viết dấu nhân ở giữa các thừa số; dấu “×” trong tích các số cũng có thể thay bằng dấu “.”.
Ví dụ:
• m × n có thể viết là m . n hay mn;
• 5 × x × y có thể viết là 5 . x . y hay 5xy;
• 125 × 731 có thể viết là 125 . 731.
9. Tính chất của phép cộng và phép nhân số tự nhiên
Với a, b, c là các số tự nhiên, ta có:
− Tính chất giao hoán:
a + b = b + a
a . b = b . a
− Tính chất kết hợp:
(a + b) + c = a + (b + c)
(a . b) . c = a . (b . c)
− Tính chất phân phối của phép nhân đối với phép cộng:
a . (b + c) = a . b + a . c
− Tính chất cộng với số 0, nhân với số 1:
a + 0 = a
a . 1 = a.
10. Phép trừ và phép chia hết
Ở Tiểu học ta đã biết cách tìm x trong phép toán b + x = a; trong đó a, b, x là các số tự nhiên, a ≥ b.
Nếu có số tự nhiên x thỏa mãn b + x = a, ta có phép trừ a – b = x và gọi x là hiệu quả của phép trừ số a cho số b, a là số bị trừ, b là số trừ.
Tương tự với a, b là các số tự nhiên, b ≠ 0, nếu có số tự nhiên x thỏa mãn bx = a, ta có phép chia a : b = x và gọi a là số bị chia, b là số chia, x là thương của phép chia số a cho số b.
Chú ý: Phép nhân cũng có tính chất phân phối đối với phép trừ:
a . (b − c) = a . b – a . c (b > c)
11. Lũy thừa
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.
an = a . a ….. a (n thừa số a) (n ∉N* )
Ta đọc an là “a mũ n” hoặc “lũy thừa bậc n của a”.
Số a được gọi là cơ số, n được gọi là số mũ.
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
Đặc biệt, a2 còn được đọc là “a bình phương” hay “bình phương của a”.
a3 được đọc là “a lập phương” hay “lập phương của a”.
Quy ước: a1 = a.
12. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
am . an = am + n.
13. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.
am : an = am – n (a ≠ 0; m ≥ n ≥ 0).
Quy ước: a0 = 1 (a ≠ 0).
14. Thứ tự thực hiện phép tính
Khi thực hiện các phép tính trong một biểu thức:
− Đối với biểu thức không có dấu ngoặc:
+ Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
− Đối với biểu thức có dấu ngoặc:
+ Nếu biểu thức có các dấu ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính trong dấu ngoặc tròn trước, rồi thực hiện phép tính trong dấu ngoặc vuông, cuối cùng thực hiện phép tính trong dấu ngoặc nhọn.
15. Sử dụng máy tính cầm tay
− Nút mở máy:
− Nút tắt máy:
− Các nút số từ 0 đến 9.
− Nút dấu cộng, dấu trừ, dấu nhân, dấu chia.
− Nút dấu “=” cho phép hiện ra kết quả trên màn hình số.
− Nút xóa (xóa số vừa đưa vào bị nhầm):
− Nút xóa toàn bộ phép tính (và kết quả) vừa thực hiện:
− Nút dấu ngoặc trái và phải:
− Nút tính lũy thừa:
16. Chia hết và chia có dư
Cho hai số tự nhiên a và b, trong đó b khác 0. Ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó 0 ≤ r < b. Ta gọi q và r lần lượt là thương và số dư trong phép chia a cho b.
− Nếu r = 0 tức a = b . q, ta nói a chia hết cho b, kí hiệu a ⋮ b và ta có phép chia hết a : b = q . a
− Nếu r ≠ 0, ta nói a không hết cho b, kí hiệu a ⋮̸ b và ta có phép chia có dư.
17. Tính chất chia hết của một tổng
Tính chất 1
Cho a, b, n là các số tự nhiên, n khác 0.
Nếu a ⋮ n và b ⋮ n thì (a + b) ⋮ n và (a − b) ⋮ n (a ≥ b)
Nếu a ⋮ n, b ⋮ n và c ⋮ n thì (a + b + c) ⋮ n.
Tính chất 2
Cho a, b, n là các số tự nhiên, n khác 0 (a ≥ b).
Nếu a ⋮̸ n và b ⋮ n thì (a + b) ⋮̸ n và (a − b) ⋮̸ n.
Nếu a ⋮ n và b ⋮̸ n thì (a + b) ⋮̸ n và (a − b) ⋮̸ n.
Nếu a ⋮̸ n, b ⋮ n và c ⋮ n thì (a + b + c) ⋮̸ n.
Nếu trong một tổng chỉ có đúng một số hạng không chia hết cho một số, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đó.
18. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
19. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
20. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.
21. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.
22. Ước và bội
Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.
Tập hợp các ước của a được kí hiệu là Ư(a). Tập hợp các bội của a được kí hiệu là B(a).
Chú ý:
- Số 0 là bội của tất cả các số tự nhiên khác 0. Số 0 không là ước của bất kì số tự nhiên nào.
- Số 1 chỉ có một ước là 1. Số 1 là ước của mọi số tự nhiên.
- Mọi số tự nhiên a lớn 1 luôn có ít nhất hai ước là 1 và chính nó.
23. Cách tìm ước
Cách tìm Ư(a):
Ta có thể tìm các ước của a (a > 1), ta có thể lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
24. Cách tìm bội
Cách tìm B(a):
Muốn tìm bội của số tự nhiên a khác 0, ta có thể nhân a lần lượt với 0, 1, 2, 3, ...
Chú ý:
Bội của a có dạng tổng quát là a . k với k ∈N. Ta có thể viết:
�(�)={� . �|�∈ℕ}.
25. Số nguyên tố. Hợp số
− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
− Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn hai ước.
Ví dụ:
+ Số 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.
+ Số 15 có bốn ước là 1; 3; 5; 15 nên 15 là hợp số.
Lưu ý: Số 0 và số 1 không là số nguyên tố cũng không là hợp số.
26. Phân tích một số ra thừa số nguyên tố
a. Thế nào là phân tích một số ra thừa số nguyên tố?
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Chú ý:
− Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
− Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
− Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.
b. Cách phân tích một số ra thừa số nguyên tố
Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc.
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Chú ý: Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.
Cách 2: Phân tích một số ra thừa số nguyên tố theo sơ đồ cây.
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
27. Ước chung
- Một số được gọi là ước chung của hai hay nhiều số nếu nó là ước của tất cả các số đó.
- Tập hợp các ước chung của hai số a và b kí hiệu là ƯC(a, b).
x ∈ ƯC(a, b) nếu a ⋮ x và b ⋮ x.
- Tương tự, tập hợp các ước chung của a, b, c kí hiệu là ƯC(a, b, c).
x ∈ ƯC(a, b, c) nếu a ⋮ x, b ⋮ x và c ⋮ x.
Cách tìm ước chung của hai số a và b:
- Viết tập hợp các ước của a và của b: Ư(a), Ư(b).
- Tìm những phần tử chung của Ư(a) và Ư(b).
28. Ước chung lớn nhất
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
Kí hiệu ước chung lớn nhất của a và b là ƯCLN(a, b).
Tương tự, ước chung lớn nhất của a, b và c là ƯCLN(a, b, c).
Nhận xét: Tất cả các ước chung của hai hay nhiều số đều là ước của ƯCLN của các số đó.
Ví dụ:
ƯC(16, 24) = {1; 2; 4; 8} nên ƯCLN(16, 24) = 8, vì 8 là số lớn nhất trong số các ước chung của 16 và 24. Các ước chung của 36 và 45 là 1; 2; 4; 8 đều là ước của 8.
Nhận xét: Với mọi số tự nhiên a và b, ta có:
ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.
Ví dụ: ƯCLN(9, 1) = 1; ƯCLN(5, 18, 1) = 1.
29. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Quy tắc:
Muốn tìm ƯCLN của của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
Chú ý: Hai số có ƯCLN bằng 1 gọi là hai số nguyên tố cùng nhau.
Ví dụ: ƯCLN(15; 23) = 1 nên 15 và 23 được gọi là hai số nguyên tố cùng nhau.
30. Ứng dụng trong rút gọn về số tối giản
Rút gọn phân số: Chia cả tử và mẫu cho ước chung khác 1 (nếu có) của chúng.
Phân số tối giản: a/b là phân số tối giản nếu ƯCLN(a, b) = 1.
Đưa một phân số chưa tối giản về phân số tối giản:
Chia cả tử và mẫu cho ƯCLN(a, b).
31. Bội chung
Một số được gọi là bội chung của hai hay nhiều số nếu nó là bội của tất cả các số đó.
• Kí hiệu tập hợp các bội chung của a và b là BC(a, b).
• Tương tự, tập hợp các bội chung của a, b, c là BC(a, b, c).
Cách tìm bội chung của hai số a và b:
- Viết tập hợp B(a) và bội B(b).
- Tìm những phần tử chung của B(a) và B(b).
32. Bội chung nhỏ nhất
Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.
Kí hiệu bội chung nhỏ nhất của a và b là BCNN(a, b).
Tương tự, bội chung nhỏ nhất của a, b và c là BCNN(a, b, c).
Nhận xét: Tất cả các bội chung của a và b đều là bội của BCN(a, b). Mọi số tự nhiên đều là bội của 1.
Do đó, với mọi số tự nhiên a và b (khác 0) ta có:
BCNN(a, 1) = a;
BCNN(a, b, 1) = BCNN(a, b).
33. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Quy tắc:
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Chú ý:
• Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.
• Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.
34. Ứng dụng trong quy đồng mẫu các phân số
Quy tắc:
Muốn quy đồng mẫu số nhiều phân số ta có thể làm như sau:
Bước 1: Tìm một bội chung của các mẫu số (thường là BCNN) để làm mẫu số chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu số (bằng cách chia mẫu số chung cho từng mẫu số riêng).
Bước 3: Nhân tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.
Xem thêm lời giải bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Chân trời sáng tạo
- Soạn văn lớp 6 (ngắn nhất) - Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 6 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 6 - Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn 6 - Chân trời sáng tạo
- Văn mẫu lớp 6 – Chân trời sáng tạo
- Giải sgk Địa Lí 6 – Chân trời sáng tạo
- Giải sbt Địa Lí 6 – Chân trời sáng tạo
- Lý thuyết Địa Lí 6 – Chân trời sáng tạo
- Giải sgk Lịch sử 6 – Chân trời sáng tạo
- Giải sbt Lịch sử 6 – Chân trời sáng tạo
- Lý thuyết Lịch sử lớp 6 – Chân trời sáng tạo
- Giải sgk GDCD 6 – Chân trời sáng tạo
- Giải sbt GDCD 6 – Chân trời sáng tạo
- Lý thuyết GDCD 6 – Chân trời sáng tạo
- Giải sgk Công nghệ 6 – Chân trời sáng tạo
- Giải sbt Công nghệ 6 – Chân trời sáng tạo
- Lý thuyết Công nghệ 6 – Chân trời sáng tạo
- Giải sgk Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 6 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 6 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 6 Friends plus đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Friends plus
- Giải sbt Tiếng Anh 6 - Friends plus
- Bài tập Tiếng Anh 6 Friends plus theo Unit có đáp án