Giải Toán 6 Bài tập cuối chương 3 - Chân trời sáng tạo

Toán lớp 6 trang 93 Câu 1

Hình thoi có độ dài hai đường chéo lần lượt là 50 m và 60 m thì diện tích là:

(A) 300

(B) 3 000

(C) 1 500

(D) 150

Lời giải:

Diện tích hình thoi đã cho là: $50.60:2=1500m^2$

Chọn C.

Toán lớp 6 trang 93 Câu 2

Hình thang cân có độ dài cạnh đáy và chiều cao lần lượt là 40 m, 30 m, 25 m, có diện tích là:

(A) 1 750

(B) 175

(C) 875

(D) 8 750

Lời giải:

Diện tích hình thang cân là: $\left(40+30\right).25:2=875m^2$

Chọn C.

Toán lớp 6 trang 93 Câu 3

Hình bình hành có chiều dài một cạnh và chiều cao tương ứng lần lượt là 70 dm và 50 dm có diện tích là:

(A) 35

(B) 3 500

(C) 17,5

(D) 350

Lời giải:

Diện tích hình bình hành là: $70.50=3500\left(d{m}^2\right)$

Đổi $3500d{m}^2=35m^2$

Chọn A.

B. Phần tự luận

Toán lớp 6 trang 93 Bài 1

Em hãy vẽ các hình sau đây:

a) Tam giác đều có cạnh là 5 cm.

b) Hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.

c) Hình vuông có cạnh 3 cm.

d) Hình bình hành có hai cạnh liên tiếp là 6 cm, 8 cm và chiều cao bằng 4 cm.

e) Hình thoi có cạnh dài 5 cm.

Lời giải:

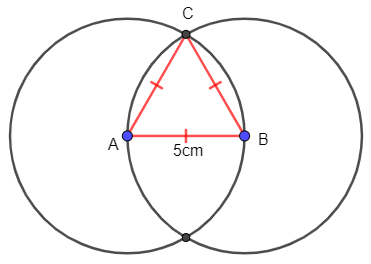
a) Tam giác đều có cạnh là 5 cm

- Vẽ đoạn thẳng AB = 5 cm.

- Vẽ đường tròn tâm A, bán kính 5 cm; vẽ đường tròn tâm B bán kính 5 cm.

- Hai đường tròn cắt nhau ở C, ta được tam giác đều ABC cạnh 5 cm.

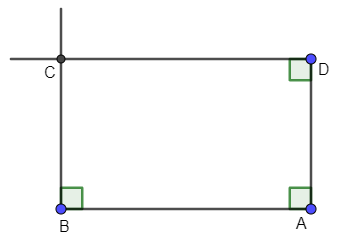
b) Hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.

- Vẽ đoạn thẳng AB = 5 cm, AD = 3 cm sao cho AB vuông góc với AD.

- Vẽ đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AD tại D.

- Hai đường thẳng này cắt nhau tại C ta được hình chữ nhật ABCD thỏa mãn yêu cầu.

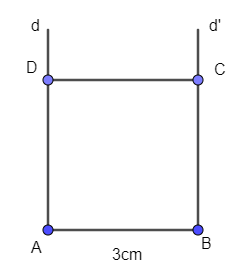
c) Hình vuông có cạnh 3 cm.

- Vẽ đoạn thẳng AB = 3 cm.

- Vẽ hai đường thẳng d, d’ lần lượt vuông góc với AB tại A và B.

- Trên đường thẳng d lấy điểm D, trên đường thẳng d’ lấy điểm C sao cho AD = BC = 3 cm.

- Nối C với D ta được hình vuông ABCD có cạnh 3 cm.

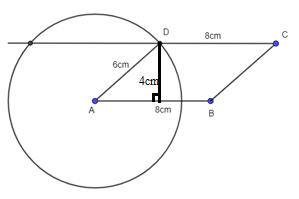
d) Hình bình hành có hai cạnh liên tiếp là 6 cm, 8 cm và chiều cao bằng 4 cm.

- Vẽ đoạn thẳng AB = 8 cm.

- Vẽ đường thẳng d song song với AB cách AB một khoảng bằng 4 cm.

- Vẽ đường tròn tâm A bán kính 6 cm. Đường tròn này cắt đường thẳng d tại điểm D.

- Trên đường thẳng d lấy đoạn thẳng DC = 8 cm.

- Nối C với B ta được hình bình hành ABCD thỏa mãn yêu cầu bài toán.

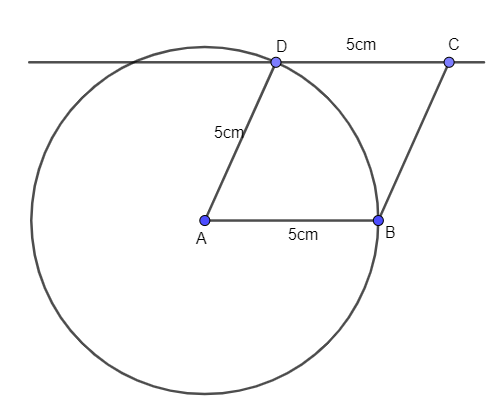
e) Hình thoi có cạnh dài 5 cm.

- Vẽ đoạn thẳng AB = 5cm.

- Vẽ đường tròn tâm A bán kính 5 cm. Trên đường tròn này lấy điểm D.

- Từ D vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm C sao cho DC = 5 cm.

- Nối C với B ta được hình thoi ABCD có cạnh 5 cm.

Toán lớp 6 trang 93 Bài 2

Hãy cắt 3 hình như hình dưới đây và ghép lại để được một hình vuông

Lời giải:

Sau khi cắt ta ghép lại thành hình vuông như sau:

Toán lớp 6 trang 93 Bài 3

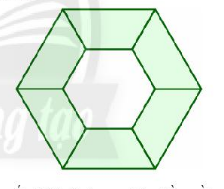
Hình đưới đây gồm các hình nào?

Lời giải:

Hình đã cho gồm các hình: Hình tam giác đều, hình thoi, hình thang cân và hình lục giác đều được xác định như sau:

- Hình tam giác đều

- Hình thoi

- Hình thang cân

- Hình lục giác đều

Toán lớp 6 trang 93 Bài 4

Hãy cắt ghép 5 hình bình hành sao cho khi ghép lại tạo thành một hình bình hành

Lời giải:

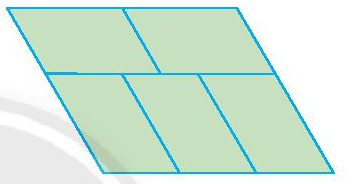
Từ 5 hình bình hành, ta sẽ ghép như hình dưới đây để tạo thành một hình bình hành.

Toán lớp 6 trang 93 Bài 5

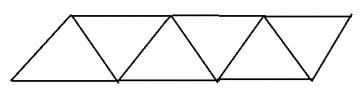
Hãy đếm xem hình dưới đây có bao nhiêu hình thang cân, bao nhiêu hình lục giác đều.

Lời giải:

Hình vẽ trên có tất cả 6 hình thang cân và 2 hình lục giác đều.

Toán lớp 6 trang 93 Bài 6

Hãy cắt 6 hình tam giác đều rồi ghép lại thành hình bình hành.

Lời giải:

Cắt 6 hình tam giác đều và ghép lại như hình vẽ dưới đây ta được hình bình hành:

Toán lớp 6 trang 93 Bài 7

Để làm một con diều, bạn Nam lấy một tờ giấy hình chữ nhật có chiều dài 60 cm, chiều rộng 40 cm để cắt thành một hình thoi như hình bên dưới. Hãy tính diện tích của con diều.

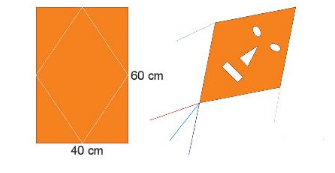
Lời giải:

Chiều dài và chiều rộng của hình chữ nhật chính là độ dài của hai đường chéo của hình thoi nên diện tích của con diều hình thoi là: $60.40:2=1200\left(c{m}^2\right)$

Vậy diện tích con diều là $1200\left(c{m}^2\right)$

Lý thuyết Toán 6 Ôn tập Chương 3 - Chân trời sáng tạo

1. Hình vuông

Hình vuông có:

+ Bốn đỉnh.

+ Bốn cạnh bằng nhau.

+ Bốn góc bằng nhau và bằng góc vuông.

+ Hai đường chéo của hình vuông bằng nhau.

Ví dụ:

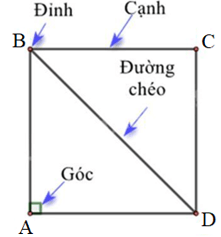
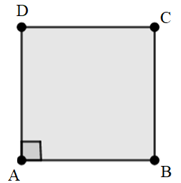
Hình vuông ABCD có:

- Bốn đỉnh A, B, C, D.

- Bốn cạnh bằng nhau: AB = BC = CD = DA.

- Bốn góc ở các đỉnh A, B, C, D là góc vuông.

- Hai đường chéo bằng nhau: AC = BD.

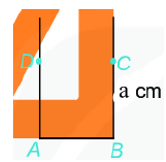
Cách vẽ hình vuông

Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng a (cm).

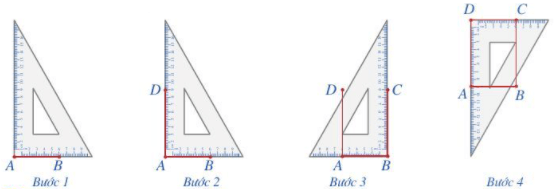
Bước 1: Vẽ đoạn thẳng AB = a (cm).

Bước 2: Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = a (cm).

Bước 3: Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = a (cm).

Bước 4: Nối C với D ta được hình vuông ABCD.

2. Tam giác đều

Tam giác đều có:

+ Ba đỉnh.

+ Ba cạnh bằng nhau.

+ Ba góc ở ba đỉnh bằng nhau.

Ví dụ:

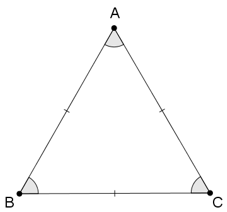
Tam giác đều ABC có:

- Ba đỉnh A, B, C.

- Ba cạnh bằng nhau: AB = BC = CA.

- Ba góc đỉnh A, B, C bằng nhau.

Cách vẽ tam giác đều

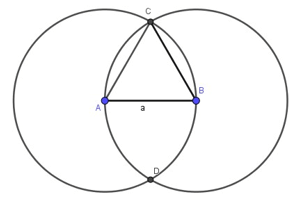
Cách vẽ tam giác đều cạnh a (cm) bằng thước và compa:

Bước 1: Dùng thước vẽ đoạn thẳng AB = a (cm).

Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.

Bước 3: Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.

Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC.

Ta được tam giác ABC đều cạnh a (như hình vẽ).

3. Lục giác đều

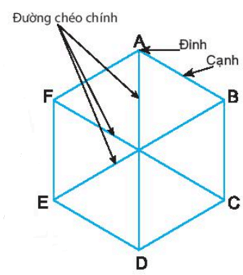
Hình lục giác đều có sáu đỉnh, sáu cạnh bằng nhau, sáu góc ở các đỉnh bằng nhau, ba đường chéo chính bằng nhau.

Ví dụ:

Lục giác đều ABCDEF có:

- Sáu đỉnh A, B, C, D, E, F.

- Sáu cạnh bằng nhau: AB = BC = CD = DE = EF.

- Sáu góc đỉnh A, B, C, D, E, F bằng nhau.

- Ba đường chéo chính bằng nhau AD = BE = CF.

4. Hình chữ nhật

Hình chữ nhật có:

+ Bốn đỉnh.

+ Hai cặp cạnh đối diện bằng nhau.

+ Hai cặp cạnh đối diện song song.

+ Bốn góc ở các đỉnh bằng nhau và bằng góc vuông.

+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Ví dụ:

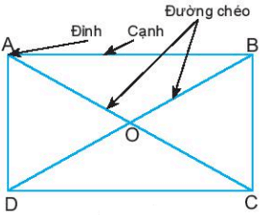
Hình chữ nhật ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.

- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:

AC = BD và OA = OC; OB = OD.

Cách vẽ hình chữ nhật

Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm.

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm.

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm.

Bước 4. Vẽ đoạn thẳng CD. Ta được hình chữ nhật ABCD.

5. Hình thoi

Hình thoi có:

+ Bốn đỉnh.

+ Bốn cạnh bằng nhau.

+ Hai cặp cạnh đối diện song song với nhau.

+ Hai đường chéo vuông góc với nhau.

Ví dụ:

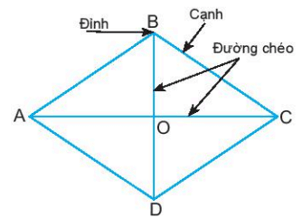
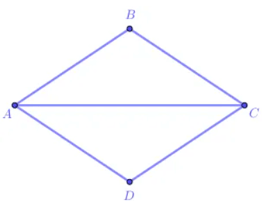
Hình thoi ABCD có:

- Bốn đỉnh A, B, C, D.

- Bốn cạnh bằng nhau: AB = BC = CD = DA;

- Hai cạnh đối AB và CD, AD và BC song song với nhau.

- Hai đường chéo AC và BD vuông góc với nhau.

Cách vẽ hình thoi

Ví dụ: Dùng thước và compa vẽ hình thoi ABCD, biết AB = 5 cm và AC = 8 cm.

Hướng dẫn giải

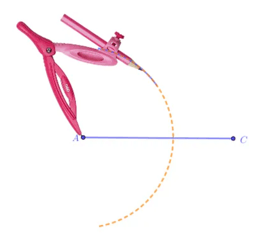
Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm.

Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm.

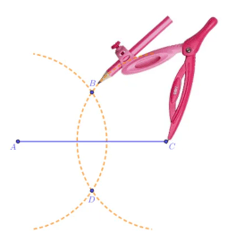
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5cm; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.

Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA. Ta được hình thoi ABCD (như hình vẽ).

6. Hình bình hành

Hình bình hành có:

+ Bốn đỉnh.

+ Hai cặp cạnh đối diện bằng nhau.

+ Hai cặp cạnh đối diện song song.

+ Hai cặp góc đối diện bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Ví dụ:

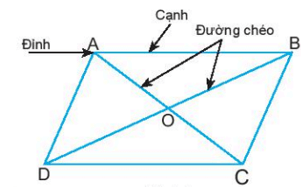
Hình bình hành ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Hai cặp góc đối diện bằng nhau: góc đỉnh A bằng góc đỉnh C; góc đỉnh B bằng góc đỉnh D.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.

Cách vẽ hình bình hành

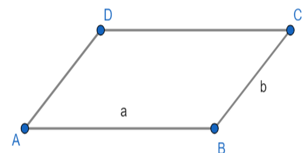
Hình bình hành ABCD có hai cạnh là a và b.

Bước 1: Vẽ đoạn thẳng AB = a (cm).

Bước 2: Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho BC = b (cm).

Bước 3: Vẽ đường thẳng đi qua A và song song với cạnh BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.

7. Hình thang cân

Hình thang cân có:

+ Hai cạnh đáy song song.

+ Hai cạnh bên bằng nhau.

+ Hai góc kề một đáy bằng nhau.

+ Hai đường chéo bằng nhau.

Ví dụ:

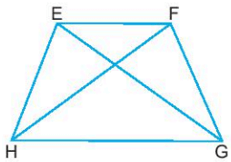
Hình thang cân EFGH có:

- Hai cạnh đáy song song: EF song song với GH.

- Hai cạnh bên bằng nhau: EH = FG.

- Hai góc kề một đáy bằng nhau: góc đỉnh E bằng góc đỉnh F, góc đỉnh G bằng góc đỉnh H.

- Hai đường chéo bằng nhau: EG = FH.

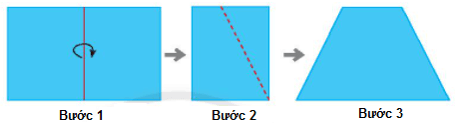
Cách gấp hình thang cân

Bước 1: Gấp đôi một tờ giấy hình chữ nhật.

Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.

Bước 3: Mở tờ giấy ra ta được một hình thang cân.

8. Chu vi và diện tích hình chữ nhật

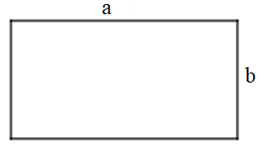
Cho hình chữ nhật có chiều dài là a, chiều rộng là b (như hình vẽ).

Chu vi của hình chữ nhật là: P = (a + b) . 2

Diện tích của hình chữ nhật là: S = a . b

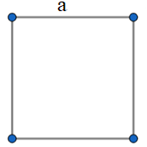
9. Chu vi và diện tích của hình vuông

Cho hình vuông có độ dài một cạnh bằng a (như hình vẽ).

Chu vi hình vuông là: P = 4a.

Diện tích hình vuông là: S = a . a = a².

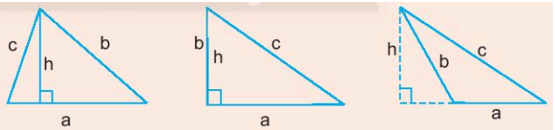
10. Chu vi và diện tích của hình tam giác

Cho tam giác có độ dài ba cạnh lần lượt là a, b, c và chiều cao tương ứng với cạnh a có độ dài là h (như hình vẽ).

Chu vi hình hình tam giác là: P = a + b + c.

Diện tích hình tam giác là: .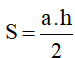

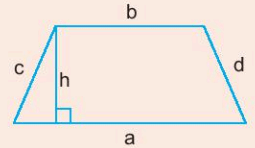
11. Chu vi và diện tích của hình thang

Cho hình thang có độ dài bốn cạnh là a, b, c, d và đường cao h (như hình vẽ).

Chu vi của hình thang là: P = a + b + c + d

Diện tích của hình thang là: .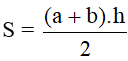

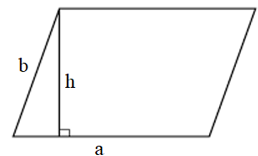
12. Chu vi và diện tích hình bình hành

Cho hình bình hành có độ dài hai cạnh là a và b, chiều cao tương ứng với một cạnh a có độ dài là h (như hình vẽ).

Chu vi hình bình hành là: P = 2(a + b).

Diện tích hình bình hành là: S = a . h

13. Chu vi và diện tích hình thoi

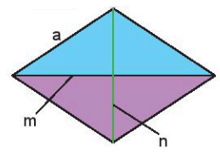
Cho hình thoi có độ dài một cạnh là a, độ dài hai đường chéo của hình thoi là m và n.

Chu vi của hình thoi là: P = 4a.

Diện tích của hình thoi là: .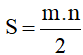

14. Chu vi và diện tích của một số hình trong thực tiễn

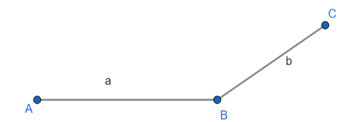
a) Tính chu vi của một số hình trong thực tiễn:

Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó.

b) Tính diện tích của một số hình trong thực tiễn:

− Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, … thì ta áp dụng công thức và tính.

− Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, …